Self-interacting random walks
One of the earliest applications of random walks was to the theory of animal movement, such as Karl Pearson's 1906 work on insect migration [link]. More recent applications include microbe locomotion. For larger animals, random walks are used to model roaming and foraging behaviour. In the context of a roaming animal searching for food, it is very natural that the animal should try to avoid places it has already visited. This leads to a random walk with memory of its past. Such self-interacting random walks have many other applications, for example as models of polymer chains.
Barycentric drift
Suppose that a random walk in $d$-dimensional space interacts with its previous trajectory through a drift in the direction from its current position either towards or away from the centre of mass of the previous trajectory. The most interesting case, from the point of view of recurrence or transience, is when the magnitude of the drift decays as a function of the distance of the current position from the centre of mass. We studied this model with Francis Comets, Mikhail Menshikov, and Stas Volkov.
Click on the buttons below for some of my work related to this class of processes.
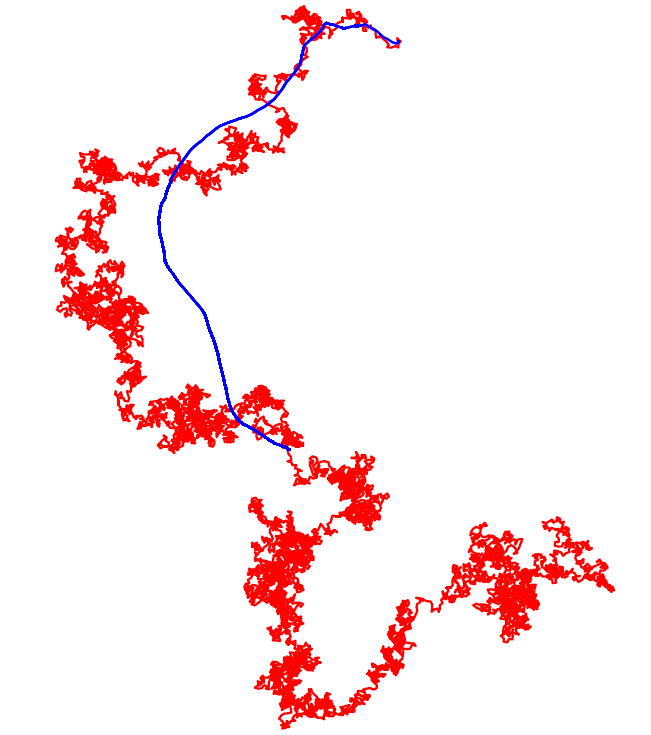
Walk with a relatively weak repulsion. The trajectory of the walk is in red, and the barycentre in blue.
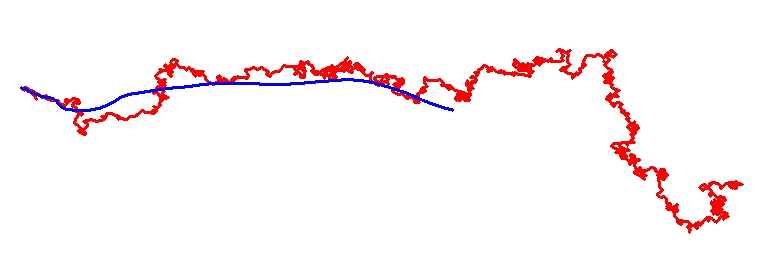
Walk with a relatively strong repulsion. The trajectory has a limiting direction, although it still has asymtotically zero speed.
Random walk avoiding its convex hull
Angel et al. introduced the following model [link]. Take a random walk in the plane which, at each step, takes its next position to be uniformly distributed on the circle centred at the current position, but excluding the convex hull of the previous trajectory (actually this is not quite the model, but gives the main idea). The conjecture is that the walk is ballistic, meaning it has a limiting direction and a limiting (positive) speed.
With Francis Comets and Mikhail Menshikov, we looked at a version of the model in which the walker only remembers the origin and the $k$ most recent past positions when constructing the convex set to avoid. We showed that the process is ballistic. (Including the origin in the convex set to be excluded is crucial to this result.) In the case $k=1$ (when the excluded set is generically a triangle) the asymptotic speed can be computed explicitly, and it is $8/(9\pi^2)$. It is an open question to investigate whether a $k \to \infty$ limit can yield any information about the model avoiding its full convex hull.
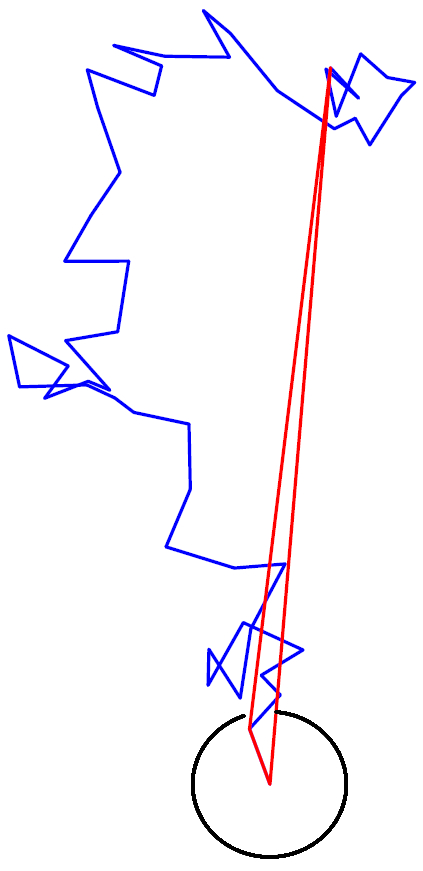
A picture of the construction for $k=1$.
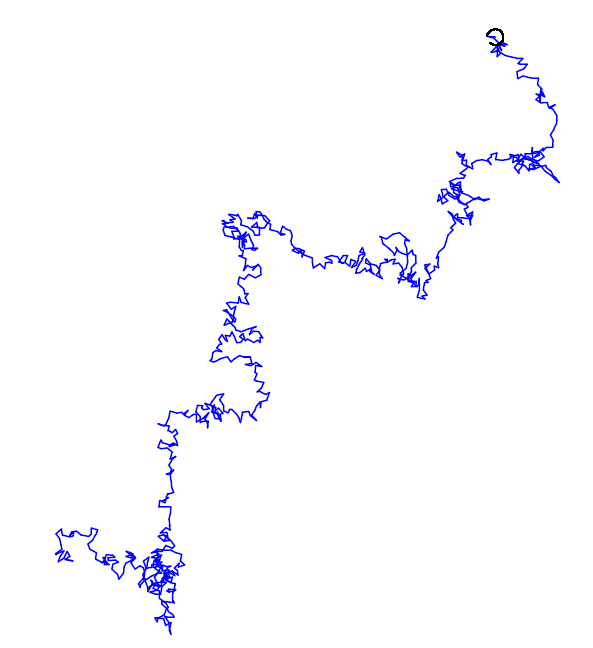
Simulation of a longer trajectory.