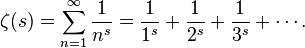Communicating Mathematics III or Project IV 05-06 (IJN)

Project IV (MATH4072) 2017-18

Analytic Number Theory:
The Riemann Zeta Function and the Prime Number Theorem

Jens Funke

Description

Prime numbers are the atoms of the integers. Every integer can be uniquely factored into primes. Since the days of Euclid we know that there are infinitely many primes. However, questions like the distribution of primes are mysterious and notoriously difficult. For example, the prime numbers between 9.999.900 and 10.000.000 are

9.999,901, 9.999.907, 9.999.929, 9.999.931, 9.999.937

9.999.943, 9.999.971, 9.999.973, 9.999.991,

whereas between 10.000.000 and 10.000.100 we only have

10.000.019 10.000.079.

However, in 1792, the 15 year old Gauss, while studying tables of logarithm, observed that π(x), the number of prime numbers less or equal a real number x, while `locally' rather randomly, satisfies `globally' a striking smoothness:

π(x) ∼ ln(x)/x,

for x large. That is, for large x, the function ln(x)/x approximates π(x) very well. (In fact, Gauss discovered an even better approximation using the so called logarithmic integral Li(x)).
This assertion is known as the PRIME NUMBER THEOREM (PNT) and was finally proven more than 100 years later in 1896 independently, by J. Hadamard and C. de la Vallee Poussin. They employed methods of complex analysis. More precisely, they studied the famous Riemann ζ-function, which was introduced by Riemann in his seminal 1859 paper. It is initially defined for a complex variable s with real part Re(s)>1 by the infinite series

$\zeta(s) = \sum_{n=1}^\infty \frac{1}{n^s} = \frac{1}{1^s} + \frac{1}{2^s} + \frac{1}{3^s} + \cdots. \!$

Riemann showed that the zeta-function has a meromorphic continuation to the whole complex plane and established the connection of the zeros of ζ with the distribution of primes. The Riemann Hypthesis asserts that the only (non-trivial) zeros of ζ are all concentrated on the vertical line Re(s)=1/2. This is in turn equivalent to an enormous strengthening of the prime number theorem. Namely, it gives a precise estimate of the error of approximating π(x) by Li(x).

In this project, we plan to study Riemann Zeta Function and the Prime Number Theorem. In addition, we also consider Dirichlet's Theorem on primes in an arithmetic progression, which initiated analytic number theory in 1837, and also the analytic class number formula for quadratic fields.

Prerequisites

ENT II, Number Theory II
Enthusiasm for Complex Analysis

Resources

As inspirational reading we recommend the article by

Don Zagier: "The first 50 million prime numbers" (PDF), Math. Intelligencer (Springer) 0, 7-19,

There are many books on the subject. For the moment we mention

H. Iwaniec and E. Kowalski, Analytic Number Theory, American Mathematical Society 2004, ISBN 0821836331 (more advanced)

A.E. Ingham, The distribution of prime numbers. Cambridge University Press 1990, ISBN 0521397898 (the classic book)

H.M. Edwards, Riemann's Zeta function. Dover 2001. (Another classic)

G.J.O Jameson, The prime number theorem. Cambridge University Press 2003, ISBN 0521891108 (very accessible)

email: J Funke