Description
This project aims to develop the basic theory of algebraic varieties (mainly over an algebraically closed field $K$, like the complex numbers). These are the classical objects of study in algebraic geometry, which is a major area of modern mathematics influencing representation theory, number theory, and many other fields.
A variety is essentially a curve, surface or higher dimensional geometric object in $K^n$, which is defined by the zeros of a system of polynomials in $n$ variables $x_1,\dots,x_n$, with coefficients in $K$. On the one hand we have these geometric subsets of $K^n$, and on the other we have the ring $$K[x_1, ..., x_n]/I,$$ where $I$ is the ideal generated by the polynomials which define the variety. This is called the (affine) coordinate ring of the variety, and the variety and the coordinate ring essentially determine each other. The aim is to understand this interplay between geometry and algebra. For example, if $K=\mathbb{R}$ the polynomial $f(x,y)=y-x^2$ defines the familiar parabola in the real plane:
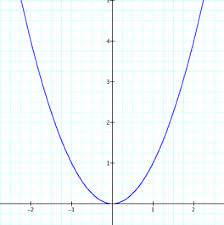
The coordinate ring in this case is $\mathbb{R}[x,y]/(y-x^2)$. If we change $\mathbb{R}$ to $\mathbb{C}$ here we get a geometric object which lives in two complex (or four real) dimensions. Projecting it down to three dimensions and using colours to indicate the fourth dimension, the geometric object corresponding to the ring $\mathbb{C}[x,y]/(y-x^2)$ looks like
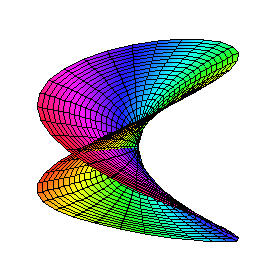
Topics for further individual study include, schemes, linear algebraic groups, counting points on varieties over finite fields (this is part of number theory).
Prerequisites
Algebra IIResources
- M. Reid, Undergraduate Commutative Algebra
- M. Reid, Undergraduate Algebraic Geometry
- D. Arapura, A pre-introduction to algebraic geometry by pictures
- K. E. Smith et. al., An Invitation to Algebraic Geometry (this will be our main source)
- W. Fulton, Algebraic
Curves (can be used as a complement to Smith's
book and is freely available here)