Description

This project will look at how to decompose a vector field as a sum of mutually orthogonal parts. Such a decomposition is invaluable in fluid dynamics, electromagnetism, plasma physics, and many other applications (for example, computer visualisation). Mathematically, it allows you to answer questions like whether a given vector field is the gradient of some function, or the curl of another vector field? Or does there exist a non-zero vector field that is divergence-free, curl-free and orthogonal to the boundary?

There are various ways to do such a decomposition. The most well-known, called the Helmholtz Decomposition Theorem, says that any (suitably well-behaved) vector field \({\bf u}\) on \(\mathbb{R}^3\) may be written as \({\bf u} = \nabla\Phi + \nabla\times{\bf A}\). In other words, as a sum of a curl-free part and a divergence-free part. But in general it is possible to decompose a vector field into more than two orthogonal pieces (the so-called Hodge Decomposition Theorem), and this turns out to be intimately connected with the nature of the domain you are considering (e.g. vector fields inside a sphere, or a torus, etc.).

This project will look into these kind of decompositions, and how they are proven. You will be encouraged to produce good illustrative examples, and to write a clear and logical exposition of the ideas at 3H level.

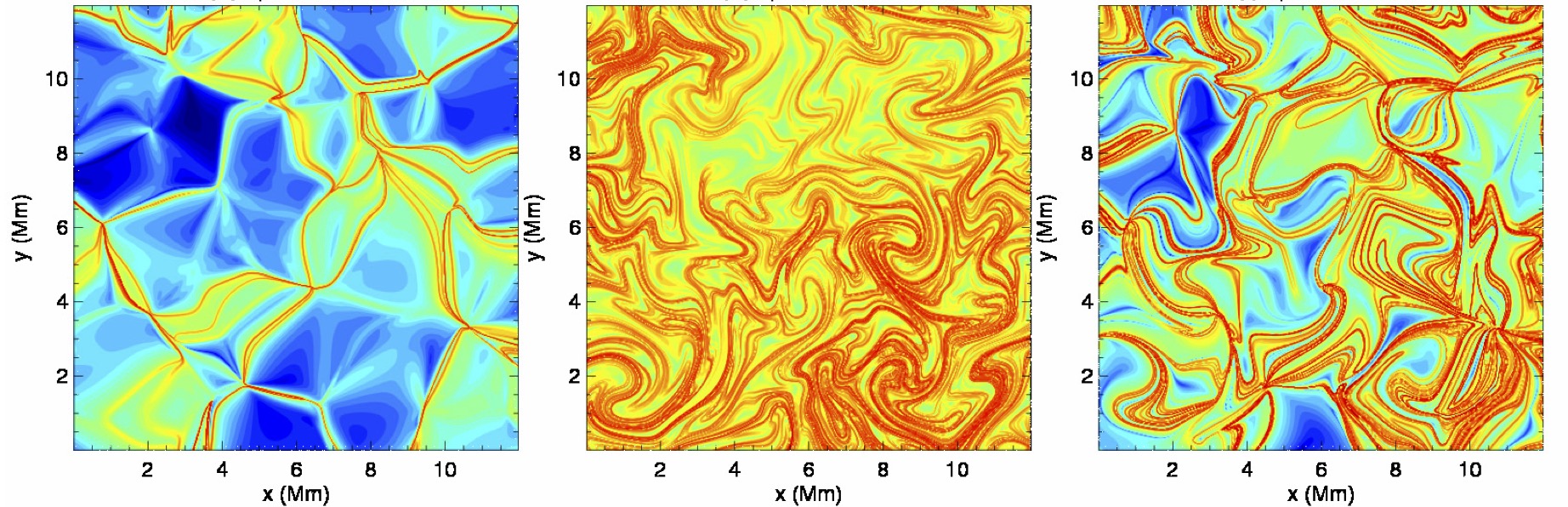
Above: an example application from my research in fluid dynamics. Here the vector field is a two-dimensional velocity field modelling convection on the Sun's surface. The pictures don't show the vectors directly, but rather a measure of how much nearby particles diverge from one another when they move according to this velocity field. Left if we take only the curl-free component, middle only the divergence-free component, and right the total velocity field.

Prerequisites

The only requirement is Analysis in Many Variables II (or alternatively PHYS2611).

Resources

The basic Helmholtz theorem is in many books about applied maths (e.g. Chapter 1 of Arfken and Weber), and information is easily obtained by googling (e.g., these notes). A useful survey paper about the various decompositions is Bhatia et al. (2013). There is an excellent (but not too technical) exposition of the Hodge Decomposition Theorem in Cantarella, DeTurck and Gluck (2002).