Description

This project will investigate mathematical models for the generation of large-scale magnetic fields in conducting fluids like the interiors of stars or planets. This remains a longstanding problem because it relies on a two-way interaction: fluid motion can stretch and amplify the magnetic field, but magnetic forces in turn feed back on the fluid. We will focus on the kinematic problem where the fluid motion is imposed and these back reactions are neglected. The question then is: will a given fluid flow amplify the magnetic field?

No prior knowledge of fluid mechanics or Maxwell's equations (for the magnetic field) is required, as we will start by reviewing the MHD (magnetohydrodynamic) equations that govern this system. We will then explore some of the classic results in the field, such as Cowling's anti-dynamo theorem and Parker's mean-field dynamo.

There will be ample scope to vary the direction of the project to suit your own interests. Some possible avenues to explore:

• Flux-transport dynamo models for the Sun's magnetic cycle.
• Low-order dynamo models where the full PDEs are approximated by ODE models (or even one-dimensional maps) that seek to understand the underlying dynamics.
• Fast dynamos and the stretch-twist-fold process.

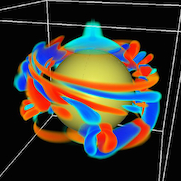A flux transport simulation of the Sun's dynamo (from here).

Prerequisites

The only essential prerequisite is Analysis in Many Variables II. Both Special Relativity & Electromagnetism II and Continuum Mechanics III would be useful, and Dynamical Systems III would be relevant specifically for the low-order models. There is good scope for numerical work in Python, but specific knowledge beyond the first-year programming course will not be assumed.

Resources [online]

There is a vast literature on dynamo theory. Good starting points would be the overview articles on The solar dynamo (Choudhuri) or Solar dynamo theory (Charbonneau), or Chapter 8 of the book Magnetohydrodynamics of the Sun (Priest). There is a good set of (graduate) lecture notes by Jones, and a useful textbook by Davidson. For much more detail, see the recently updated textbook Self-exciting fluid dynamos (Moffatt & Dormy).