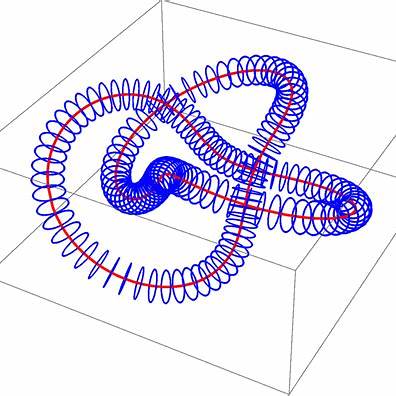
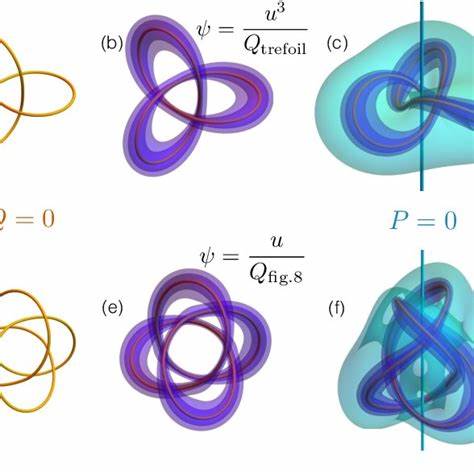
This project explores the geometry and topology of knotted vector fields, such as those arising in fluid flows and magnetic fields, using the framework of contact geometry. These systems support complex topological structures—knots, links, and braids—that can be studied analytically via differential forms, and visualised through explicit constructions.
Contact structures offer a natural language to describe three-dimensional vector fields that are everywhere non-integrable. Notably, certain solutions to the Euler and Maxwell equations can exhibit knotted field lines, and contact forms give powerful tools for classifying and analysing these configurations. This topic connects deep mathematical ideas to physical systems such as plasmas, fluids, and optical vortices.
The project will involve techniques from differential geometry, topology (particularly knot theory), and partial differential equations. Students may investigate existence theorems for knotted fields, explore the role of helicity, and construct explicit examples. While the focus will be theoretical (“book work”), there is room for numerical illustration or symbolic computation (e.g., in Python or Mathematica) for students who are keen.


This project is well suited for students who enjoy abstract mathematics and are interested in how geometry and topology apply to physical models. Experience with vector calculus, PDEs, or introductory differential geometry/topology will be useful. Some prior exposure to knot theory or contact structures is helpful but not required.