Project III (MATH3382) 2021-22

Embedding random walks in a Brownian motion

An interplay between Brownian paths and finite samples.

C. da Costa

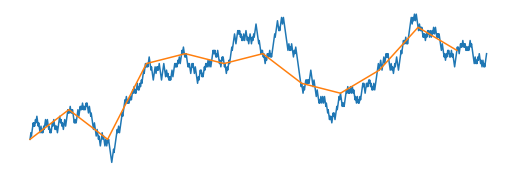
We start with a vague question. Can one use the Brownian motion to sample the sum of i.i.d. random variables that converge to the Brownian motion?

This is a problem of embedding of random walks. It can be illustrated as follows:


Skorohod embedding of random walk

Fig. - A random walk can be embedded in a Brownian motion.


The Skorohod embedding problem is the following: given a random variable \(X\) with finite second moment and zero mean, can one find a Brownian motion \((B(t),t\geq 0)\), and a stoping time \(T\) such that \( E(T) <\infty\) and \( B(T)\) have the same distribution of \(X\)?

Ever since it was proposed, in 1961, this problem has received at least 21 different solutions. The reason for continous refinements on this problem is its relation with the invariance principle. In a few words, the invariance principle states that any sum of independent random variables with finite second moment converges, after centering and rescaling, to the Brownian motion.

To see the power of this theory, we show how to obtain the Central limit theorem from the weak Law of Large Numbers in combination with the Skorohod embedding. Simply said, let \(Y_n = \sum_{i = 1}^n X_i\) be a sum of \(n\) i.i.d. mean zero random variables with \(E[X_1^2] = \sigma^2\). Now, if \(T_1\) is such that \(B_{T_1} =X_1\) and \(E[T_1]< \infty\) then,

\(E[T_1] = E[B_{T_1}^2] = E[X_1^2] = \sigma^2\).

Let \(B^{(1)}_t := B_{T_1 + t} - B_{T_1}\) and note that \(B^{(1)}_t,t \geq 0\) is again a Brownian motion. Let \(T_2\) be such that \(B^{(1)}_{T_2} = X_2\). We continue in this manner and define stopping times \(T_1,\ldots,T_n\) such that

\(B_{S_k} = X_1 + \ldots X_k = Y_k\) where \(S_k := T_1 + \ldots +T_k\).

Now, \(S_n = T_1 + \ldots +T_n\) and by the weak Law of Large Numbers \(n^{-1}S_n \to \mathbb{E}[T_1] = \sigma^2 \). Finally, note that the process \(W^{(n)}_t: = \frac{B_{nt}}{\sqrt{n}}\) is again a Brownian motion, that \(B_{S_n} = Y_n\) and, to obtain the CLT, observe that

\(\frac{Y_n}{\sqrt{n}} = \frac{B_{S_n}}{\sqrt{n}} =\frac{B_{n \frac{S_n}{n}}}{\sqrt{n}} = W^{(n)}_{n^{-1}S_n} \to W^*_{\sigma^2}\).

Not only the Central limit theorem but the Law of Iterated Logarithm and Donsker's theorem may be obtained from Skorohod embedding. This method of proof yields not only the limit statements but also bounds on the rate of convergence.

In this project you will study the classical Skorohod embedding problem and it's applications which include among others

  • CLT, Donsker's theorem and the Law of Iterated Logarithm,
  • the study of \(1/2\)-stable distributions, and
  • Processes in random environments.

    • Furthermore, this problems may be studied by different methods such as

  • Martingale theory,
  • Markov Theory, and
  • Potential theory.

    • Prerequisites

    Probability II.

    Resources

  • Wikipedia: "Skorokhod's" embedding theorem.
  • Obłój, J. - The Skorokhod embedding problem and its offspring.
  • Durrett, R.- Probability theory and examples, 5th edition.

    • email: Conrado da Costa