Description

It is well known that one cannot map the surface of a sphere onto a flat plane without tearing and/or stretching, so to display a map (part of the Earth's surface) on paper or computer/phone screen, some compromises (the choice of projection) need to be made depending on the purpose of the map. This project will start by looking at different map projections and their properties.

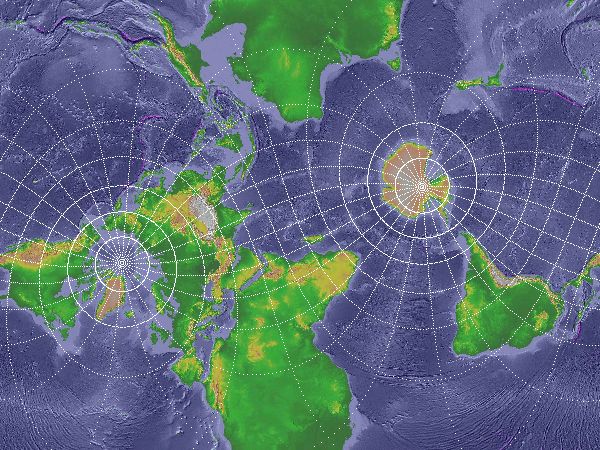
Now the surface of the earth, even "on average", is neither a perfect sphere nor an ellipsoid of revolution (an early estimate of the latter was made in Newton's Principia). In the past, this did not cause many serious problems, but recent advances in mapping (eg, GPS) technology allow us to measure distances across the globe to within a few millimetres, forcing us to re-evaluate familiar concepts such as longitude, latitude, mean sea level, etc. We will look at ways on how these can be done and the problems that arise.

There are many related problems, eg, using human population (or economic resources, etc) instead of land area as metric produces strange-looking maps which some argue are more representative or useful than traditional maps. Modern geographers are actually a big user of large-scale computations!

Pre-/Co-requisites

Both AMV2 and CA2, plus at least one of Numerical Analysis 2 or Differential Geometry 3. Facility with computers is useful to produce maps in different projections; those pursuing computational aspects will obviously need programming skills. A love of maps would help!

Resources

• Feeman 2002: Portraits of the earth: a mathematician looks at maps, American Math. Soc.
• Generic Mapping Tools: used to generate the above map and much more.
• geographiclib: Python library for cartographic computations.