Description

Shear flows arise when adjacent layers of fluid move parallel to each other at different speeds, creating velocity gradients. These flows are common in a wide range of physical systems, including atmospheric jets, the ocean, astrophysical disks, blood vessels, and various industrial applications. Under certain conditions, the velocity gradient can destabilize the flow, leading to the growth of disturbances and eventually to turbulence. Understanding when and how turbulence arises is a central question in fluid dynamics.

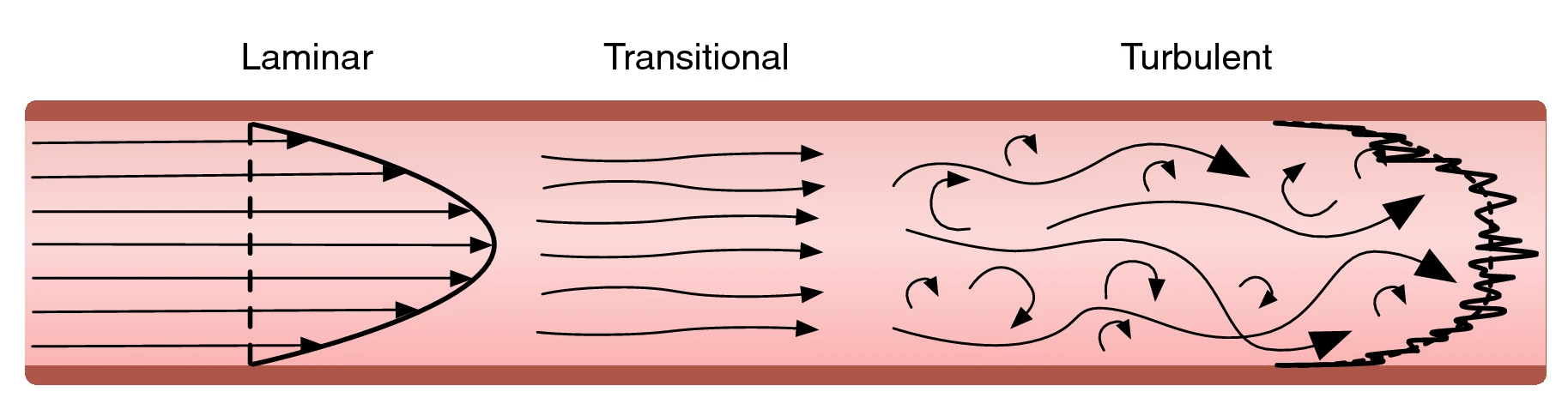
In this project, we will explore the mathematical and physical mechanisms that lead to instability in shear flows. We will begin with a review of the governing equations and the fundamentals of linear stability theory, before deriving classic criteria used to assess the stability of shear flows. Following this, students will be encouraged to pursue a specific area of interest. Some possible directions are listed below, though students are welcome to explore alternative topics aligned with their own interests:

• The interaction of shear flow instabilities with stratification, rotation or magnetic fields.
• Applications of shear flow instabilities (e.g., in stellar raidative zones or the ocean).
• Extensions of classical results to the case of non-newtonian fluids.
• Numerical solutions of the Orr-Sommerfeld equation).

Prerequisites

Fluid Mechanics III is required. It is expected that most projects in this area will require some numerical computation in Python (or similar) but only basic knowledge of programming is required. An eagerness to learn and try things out is more important! Specific knowledge beyond the first-year programming course will not be assumed.

Resources

There is a vast literature on shear instabilities. Here is a sample you may look at to get started:

• Textbook by Drazin & Reid (classic textbook on Hydrodynamic Stability)
• Lecture notes by Fabian Waleffe from the Woods Hole Geophysical Fluid Dynamics Program.
• Research article by Park et al. (2020) on shear instabilities in stars.

For more information email: Laura Currie