Project III 2022-23
Instantons in Quantum Mechanics
Madalena Lemos (email)
Description
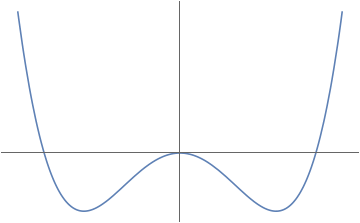Classically if you have a particle in a double well potential as the one pictured on the right there is no trajectory for a particle to travel from one well to the other. Quantum mechanically, however, a particle can tunnel from one to the other -- these tunneling processes are described by Instantons . In this project you will see an alternative approach to quantum mechanics, called path integral quantization, that will make it easy to compute the tunneling probability. For that you will first recall Lagrangians, and study the principle of least action. Then, after getting acquainted with the path integral you will see instantons as classical solutions to the Euclidean equations of motion with a finite action, and study examples of instantons in quantum mechanics.
Pre-requisites
- Mathematical Physics II or equivalent
Co-requisites
- Quantum Mechanics III or equivalent
References
- The Feynman lectures on physics, The Principle of Least Action
- Feynman and Hibbs, Quantum Mechanics and Path Integrals -- chapters 1, 2
- T. Lancaster, S. Blundell, Quantum Field Theory for the Gifted Amateur -- chapters 1, 23, 50
- Coleman, Aspects of symmetry chapter 7.2