Introduction

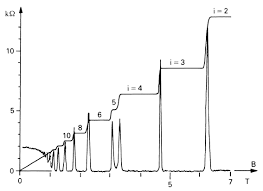
The Quantum Hall Effect is one of the most remarkable and surprising experimental results in physics. The above figure shows an experimental plot of a macroscopic quantity known as resistivity as a function of the magnetic field. Instead of a smooth curve, there are a series of plateaus where the resistivity takes values

\( \rho = \displaystyle\frac{2\pi \hbar}{e^2 \nu }\) .

where \( \nu \in \mathbb{Z}\). This result is completely independent of the properties of the material, depending only on a combination of fundamental constants of nature and the integer \( \nu \in \mathbb{Z}\). This is very surprising! We are used to the quantization of macroscopic quantities such as the energy levels of a hydrogen atom, but here we see quantization at macroscopic distances. The quest to understand and explain this result has been a rich source of new ideas in mathematical physics.

This project is to understand the theoretical underpinnings of the quantum Hall effect. This is a wonderful opportunity to deepen your understanding of quantum mechanics and explore its connections to the mathematical subject of topology. (I would like to emphasis that no prior knowledge of topology is required.)

Outline

• Term 1: You will begin by developing a good understanding of the quantum mechanical description of charged particles in an electromagnetic field and the Berry phase in quantum mechanics.

• Term 2: Building on this foundation, in the second term you will apply these ideas to explain the integer and fractional quantum Hall effects. You will also have the opportunity to explore a more advanced topic in further depth.

Prerequisites

Quantum Mechanics III

Resources

A Topological Look at the Quantum Hall Effect, Physics Today Article