DNA damage and repair
It has been estimated that due to the constant interaction with the environment every cell in a human body experiences 20,000 to 100,000 lesions per day. If left unrepaired, some of these changes can lead to unwanted mutations or even to the cell death. To protect the precious genetic information, the evolution has developed a repair mechanism, which deletes a neighbourhood of a damaged base of the DNA (grey and black in the animation below) and replaces it by the correct sequence generated from the complementary strand of the DNA. However, if two such repair processes run in close vicinity of each other, a double strand break can occur, which is often fatal to cells.[1]
To study the effect of randomness in the system, consider a single-stranded version of the model in [1]. Namely,
a string of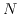 
bases, each of which can get damaged at positive rate 
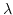and, independently of everything else happening to the system, get repaired at positive rate 
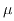; the process stops when two defects appear too close, so that their 
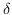-neighbourhoods intersect, resulting in a death event;
one is interested in the first moment when the process stops, starting from a completely undamaged initial configuration (in the animation below we have 
, 
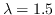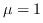and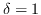 
; damaged bases are black, the neighbourhood is grey and the critically damaged bases are red).
It has been discovered [2,3] that the system exhibits a non-trivial phase transition, which is not present in the approximation considered in [1]. There are still a number of exciting open questions about this model; get in touch if interested!
[1] Karschau J, deAlmeida C, Richard MC, Miller S, Booth IR, Grebogi C, deMoura APS. (2011) A Matter of Life and Death: Modelling DNA Damage and Repair in Bacteria. Biophys J 100:814--821, doi: 10.1016/j.bpj.2010.12.3713
[2] Campion J, Dessain T, Hryniv O. Stochastic modelling of DNA damage and repair. [in preparation]
[3] Dessain T, Hryniv O. Phase transition in a stochastic model of DNA damage and repair. [in preparation]
Back
