| Erwin Bolthausen (University of Zurich) | Thursday 5th July 10:00 |
| Random walks in random environment I |
The minicourse focusses on two topics:
- A recent approach (with Ilya Goldsheid) for a
RWRE on a strip. This includes a characterization
of recurrence in terms of Lyapunov-exponents, and
a proof of Sinai-type behavior.
- An approach (with Ofer Zeitouni) on RWRE
in dimension 3 and larger in the perturbative
regime, i.e. for small disorder. This approach
is based on an investigation of exit distributions.
|
|
| Erwin Bolthausen (University of Zurich) | Saturday 7th July 09:00 |
| Random walks in random environment II |
|
|
| Erwin Bolthausen (University of Zurich) | Tuesday 10th July 09:00 |
| Random walks in random environment III |
|
|
| Krzysztof Burdzy (University of Washington) | Wednesday 11th July 16:00 |
| Pathwise uniqueness for reflecting Brownian motion |
(Joint work with R Bass)
The Skorohod stochastic differential equation,
describing reflected Brownian motion,
has a unique pathwise solution in Euclidean
domains in dimensions 3 and higher, provided
that the boundary is of class
Cb with b greater than
3/2. A counterexample for a related SDE
indicates that the result is sharp. |
|
| Francis Comets (Paris Diderot) | Wednesday 11th July 11:30 |
| On ρ-percolation and the number of polymer paths |
Joint work with Serguei Popov (U. Sao Paulo), Marina Vachkovskaia
(Unicamp)
Consider oriented Bernoulli site percolation with parameter p in
dimension 1+d . Let Qn(k) be the number of oriented path of
length n which have exactly k open vertices. We prove that
Σk ≥ n ρ = exp n[α(ρ)+o(1)]
a.s. as n tends to infinity, for all ρ except maybe two values.
The function α(.) is deterministic and relates to
the free energy of directed polymers in random environment.
This function has an explicit expression for d ≥ 3 and ρ not
too far from p. Moreover, we obtain an equivalent for Qn(kn)
for kn∼ n ρ, ρ close to p and d>2.
|
|
| Burgess Davis (Purdue University) | Tuesday 10th July 16:00 |
Initial weights and recurrence in vertex reinforced jump
processes |
An assignment of positive numbers (weights) w(v) to each
vertex v of a graph can be used to define a discrete time nearest neighbor
random walk via the rule that jump probabilities are proportional to weights.
Such an assignment can also be used to define a continuous time vertex
reinforced jump processes in which jumps to a nearest neighbor v occur at the
time dependent rate w(v) plus the total time up to t that the process has spent at v. On some graphs there are weighting schemes which correspond to transience in discrete time and recurrence in continuous time. Noah Dean has recently shown that for the nonnegative integers this is not the case. I will discuss Dean’s work and related work of Stanislav Volkov and myself.
|
|
| Thierry Delmotte (Universite Paul Sabatier) | Tuesday 3rd July 17:15 |
| Reversible random walks in a random environment of elliptic conductances |
(Joint work with Jean-Dominique Deuschel)
This talk is about reversible random walks on Zd among random conductances on the edges which are bounded above and below by positive constants.
We try to give an overall picture of their behaviour, in particular of their regularity with some geometric intuition. |
|
| Ilya Goldscheid (Queen Mary, University of London) | Saturday 7th July 16:45 |
| Products of random transformations an RWRE |
| I shall discuss connections between properties of certain types of
non-linear random transformations and random walks in some random
environments. |
|
| Olle Haggstrom (Chalmers) | Tuesday 3rd July 16:00 |
| Markov chains in a percolation theorist's toolbox |
| Clever probabilistic arguments abound in percolation theory. A number of them involve introducing a Markov chain as a tool for studying a system that in itself involves no time dynamics. I intend this talk as a survey of such ideas, that will take us from Ted Harris' classical 1960 paper, via a number of other influential contributions, to some recent papers that I coauthored with Johan Jonasson and with Rob van den Berg and Jeff Kahn. |
|
| Martin Hairer (University of Warwick) | Tuesday 3rd July 16:45 |
| Ergodic theory for a class of non-Markovian processes |
| We consider evolution equations driven by noise that is not white in time, so that the resulting process does not have the Markov property. We show that there is an analogue in this setting to the well-known Doob-Khasminskii ergodicity criterion, provided that the driving noise saisfies a certain "quasi-Markov" property. This can be verified in many cases, including for example SDEs driving by fractional Brownian motion, which exhibit long-range memory.
|
|
| Simon Harris (University of Bath) | Tuesday 10th July 16:45 |
| Branching Brownian motion in a quadratic potential |
| We will consider a branching Brownian motion where each particle undergoes binary fission at a rate quadratic with its distance from the origin. The right most particle position and the numbers of particles following close to given paths will be discussed. Particular difficulties arise in this model as a quadratic breeding rate is critical in terms of population explosion. |
|
| Antal Jarai (Carleton University) | Saturday 7th July 17:30 |
| Some estimates on 2D percolation |
| We present some estimates on 2D critical percolation that we believe will
be useful for studying the behaviour of random walk on the incipient
infinite cluster in two dimensions. Bounds on electrical resistance are
of particular interest.
|
|
| Mark Jerrum (Queen Mary, University of London) | Wednesday 4th July 16:45 |
| Tight bounds on mixing time of Markov chains |
| Good upper bounds
on mixing time are required in the analysis of
many randomised algorithms. Tight bounds are hard
to come by, though it is well known that coupling
arguments can sometimes oblige. This talk will
concentrate on other techniques, such as
harmonic analysis or logarithmic Sobolev inequalities.
|
|
| Wilfrid Kendall (University of Warwick) | Wednesday 11th July 16:45 |
| Coupling Brownian stochastic areas |
| I will talk about recent work on how to couple Brownian motion together with all its Levy stochastic areas. |
|
| Takashi Kumagai (Kyoto University) | Friday 6th July 16:00 |
| Heat kernel estimates and Harnack inequalities for jump processes
|
(Joint work with M.T. Barlow, A. Grigor'yan and
with M.T. Barlow, R.F. Bass.)
I will talk about the relationships between the parabolic Harnack inequality,
heat kernel estimates, some geometric conditions, and some analytic conditions
for random walks with long range jumps. Unlike the case of diffusion processes,
the parabolic Harnack inequality does not, in general, imply the corresponding
heat kernel estimates. |
|
| Yves Le Jan (Université Paris Sud) | Tuesday 10th July 11:30 |
| Determinants and Markov chains |
|
|
| Vlada Limic (Université de Provence) | Monday 9th July 11:30 |
| Waiting for the attracting edge to appear |
| We consider a strongly edge reinforced walk on a locally finite graph, where it is known that almost surely an attracting edge appears eventually. This means that starting from some finite random time T the particle traverses one and the same edge, with probability 1. The goal is to study the above time T, more precisely the tails of its distribution.
It turns out that there is a universality type property: for a given strong weight reinforcement W, the tails of T corresponding to the walk on the 2-edge graph are of the same order of magnitude as those corresponding to the walk on any finite graph. Some partial results are obtained for infinite trees and general locally finite graphs. This is joint work with Codina Cotar. |
|
| Russell Lyons (Indiana University) | Wednesday 11th July 10:00 |
| Unimodularity and stochastic processes |
Stochastic processes on vertex-transitive graphs, especially Cayley graphs
of groups, have been studied for 50 years (not counting the special case of
integer lattices, which goes back hundreds of years).
The assumption of invariance under graph automorphisms plays a key role,
but investigations of the last 15 years have shown that an additional
assumption is also extremely useful.
This newer assumption is the property of unimodularity, which is equivalent
to the Mass-Transport Principle.
We shall review some well-known applications and also discuss recent work with
David Aldous.
|
|
| Terry Lyons (University of Oxford) | Friday 6th July 16:45 |
| Rapid convergence of a Markov chain with stationary measure: the heat kernel measure |
| There is an interesting non-reversible process that seems to have rapid mixing properties, and whose equilibrium measure is given by the law at time 1 of a solution to a given stochastic differential equation. The process is intriguing, because one can make many very explicit calculations, but the lack of self-adjointness makes it hard to do anything with the results of these calculations. |
|
| Jean Mairesse (CNRS, University Paris 7) | Tuesday 3rd July 12:15 |
| From random walks on groups to queueing networks |
(Joint work with T.-H. Dao-Thi, Univ. Paris 7.)
Consider a transient nearest-neighbor random walk on a plain group, i.e. a free product of a finitely-generated free group and finitely many finite groups.
Elements of the group can be set in bijection with a regular language L over the
alphabet of generators. The random walk can be viewed as a random sequence of words of L, with a local dynamic affecting only one of the extremities of the words, say the right one. We now change the model by assuming that both extremities can be modified, the right one according to the random walk mechanism, and the left one by cancellation of one symbol. If the rate at which the left end gets modified is large enough, then the model becomes a positive recurrent Markov chain on L. First, we prove that the stationary distribution exhibits a simple multiplicative form. Second, we show that the model admits a very natural interpretation in terms of queueing theory. In particular, we obtain a wide generalization of the classical theory of `product form networks`.
|
|
| Pierre Mathieu (Université de Provence) | Wednesday 4th July 12:15 |
| Random walks with random conductances |
|
|
| Mikhail V. Menshikov (Durham University) | Wednesday 11th July 12:15 |
| Periodicity for some transient random walk associated with a polling system
|
| We consider some exhaustive polling system with three nodes in its
transient regime and showed that the sequence of nodes visited by the
server is eventually periodic almost surely. To do this we construct
a dynamical system, the triangle process,which looks like some
"strange billiard".We show that this dynamical system has eventually
periodic trajectories for almost all sets of parameters
and in this case we show that the stochastic trajectories follow the
deterministic ones a.s. We also show there are infinitely many sets
of parameters where the triangle process has aperiodic trajectories
and in such cases trajectories of the stochastic model are aperiodic
with positive probability.
|
|
| Franz Merkl (University of Munich) | Wednesday 4th July 16:00 |
| Reinforced random walk on two-dimensional graphs |
| In the 1980ies, Diaconis asked whether linearly edge-reinforced random walk on Z2 is recurrent. This problem is still open.
In the talk, I shall explain a proof of recurrence for
edge-reinforced walk on a modification of Z2.
Furthermore, I shall report about recently proven bounds for the
asymptotic behaviour of linearly edge-reinforced random
walk on Z2. All results are joint work with Silke Rolle |
|
| Peter Moerters (University of Bath) | Monday 9th July 16:00 |
| Intersections of random walks in supercritical dimensions |
(Joint work with Xia Chen (Knoxville))
In high dimensions two independent simple random walks have only a finite number of intersections. In the talk I present recent progress on the problem of describing the exact upper tail behaviour of this random variable.
|
|
| Stas Molchanov (University of North Carolina) | Saturday 7th July 12:15 |
| Phase transitions in the long polymer chains |
| Transition from the globular phase to the diffusive phase for the long polymer chains in the potential field localized in space. Homopolymers and heteropolymers:
limit theorms, estimations of the free energy. |
|
| James Norris (University of Cambridge) | Thursday 5th July 11:30 |
| Stochastic flows, planar aggregation and the Brownian web |
| We study a simple growth model in two dimensions in which incoming particles
are attached to a cluster at points distributed according to the harmonic measure
at infinity, that is, the hitting distribution of a Brownian particle started at
infinity. The model is formulated as a composition of random conformal maps.
We show that, in the limit of small particle radius, the harmonic measure evolves
according to the Brownian web. This is joint work with Amanda Turner. |
|
| Robin Pemantle (University of Pennsylvania) | Monday 9th July 09:00 |
| Random processes with reinforcement I (Basic models and techniques) |
| The three lecture minicourse will address models, results and
techniques for a loosely defined collection of stochastic
processes known as "random processes with reinforcement".
Much of the material will be taken from my recent survey
paper on this subject (Probability Surveys vol. 4, 1-79),
which is in turn drawn from many sources including surveys
by M. Benaim and by B. Davis.
Roughly speaking, we call {Xt} a reinforced process if the
pair (Xt , mt) is Markov, where mt is the occupation
measure of {Xs} up to time t. After giving a number of
classical and modern examples, which imclude various
types of reinforced random walks, I will address some basic
techniques of analysis. The most general of these is the
stochastic approximation approach: a Doob decomposition
represents the process as the solution of an ODE plus noise.
By means of martingale techniques, it may be determined
when {Xt} behaves similarly to trajectories of the ODE.
Another widely used technique is to use a Poisson process
representation. Once the process {Xt} is represented as
a function of a simpler process, events of interest may
be mapped back to the simpler process and their probabilities
estimated. A third technique, less general but very powerful
when applicable, is to make use of any exchangeability
hypotheses satisfied by the process {Xt} or its increments. |
|
| Robin Pemantle (University of Pennsylvania) | Tuesday 10th July 10:00 |
| Random processes with reinforcement II (Applications of urn models) |
A number of mathematically interesting special cases of
reinforced processes have arisen out of applications.
One could in fact spend three lectures just surveying these.
I will spend just one lecture, concentrating on three major
areas of application.
(1) Statisticians have been using urn
models since the 1970's as a means of generating computationally
tractable families of prior distributions. The literature on
this is full of famous names and surprising identities.
(2) The
study of self-organization in the biological and social sciences
often has led to interesting variants of the basic Polya urn
process.
(3) Applications to evolutionary game settings tend
to be intractably complex; nevertheless, a number of rigorous
results have been obtained. |
|
| Robin Pemantle (University of Pennsylvania) | Wednesday 11th July 09:00 |
| Random processes with reinforcement III (Recent problems and results) |
| The stochastic approximation method is the chief analytic
tool used in studying reinforcement processes. The main
open problem in this area is understand what happens in
the absence of the hypothesis of noise whose standard
deviation is at least the same order as the step size.
In the first part of the lecture, I will concentrate on
results and open problems regarding this type of "slowdown".
In the second part I will describe some continuous-time
processes that arise as limits of reinforced random walks.
|
|
| Olivier Raimond (Paris-Sud) | Monday 9th July 12:15 |
| From simulated annealing to vertex-reinforced random walks. |
(Joint work with Michel Benaim)
A class of vertex-reinforced random walks is studied.
Asymptotic results are given. Under certain asumptions, the asymptotic behavior of these walks can be described in term of a certain set-valued dynamical system.
|
|
| Silke Rolles (Technical University, Munich) | Wednesday 4th July 11:30 |
| Linearly edge-reinforced random walks - a subjective overview |
| Linearly edge-reinforced random walk was introduced in 1986 by
Persi Diaconis. In the talk, I will review results ranging from
the "magic formula" discovered by Coppersmith and Diaconis in
1986 to recent results for two-dimensional graphs. |
|
| Christophe Sabot (Université Lyon) | Saturday 7th July 11:30 |
| Limit laws for random walks in random environment on Z |
| In 1975, Kesten Kozlov and Spitzer proved a limit theorem for transient one-dimensionnal random walks in random environment with null speed. It asserts that Xn, properly renormalized, converges to a stable law. The question of an explicit description of the parameters of this stable law was left open. In this talk (based on a joint work with N. Enriquez and O. Zindy) I will present a different proof of this result which leads to a description of the parameters. The case of beta environment appears to be remarkably explicit. |
|
| Akira Sakai (University of Bath) | Tuesday 10th July 17:45 |
| Critical behaviour and the limit distribution for long-range oriented percolation |
(Joint work with L.-C. Chen)
Oriented percolation on 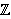 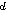 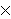 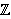 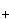 is a discrete-time analogue of the contact process, a model for the spread of an infection. Each time-oriented bond ((x,n),(y,n+1)) is either occupied with probability pD(y is a discrete-time analogue of the contact process, a model for the spread of an infection. Each time-oriented bond ((x,n),(y,n+1)) is either occupied with probability pD(y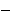 x) or vacant with probability 1 x) or vacant with probability 1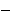 pD(y pD(y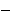 x), independently of the other bonds, where D is a probability distribution on x), independently of the other bonds, where D is a probability distribution on 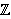 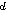 and p and p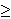 0 is the percolation parameter. We are interested in the random sets of vertices connected by occupied time-oriented bonds. It is known that the model exhibits a phase transition and critical behaviour around the phase transition point p=p 0 is the percolation parameter. We are interested in the random sets of vertices connected by occupied time-oriented bonds. It is known that the model exhibits a phase transition and critical behaviour around the phase transition point p=p . .
Fix 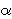 >0 and suppose that D(x) decays as |x| >0 and suppose that D(x) decays as |x| 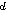  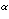 for large |x|. Let Z for large |x|. Let Z (k;n) be the Fourier transform of (k;n) be the Fourier transform of 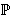  ((o,0) is connected to (x,n)), so that Z ((o,0) is connected to (x,n)), so that Z (0;n) is the expected number of vertices at time n connected from the space-time origin (o,0). We proved that Z (0;n) is the expected number of vertices at time n connected from the space-time origin (o,0). We proved that Z (0;n) for p (0;n) for p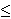 p p is asymptotically equal to a multiple of m is asymptotically equal to a multiple of m  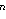 if d>2( if d>2(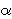 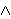 2), where m 2), where m is the radius of convergence which is 1 at p=p is the radius of convergence which is 1 at p=p . We also proved that Z . We also proved that Z (k;n) (k;n)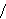 Z Z (0;n) for
p (0;n) for
p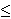 p p , with a proper scaling for k in terms of n, has a convergent subsequence to exp( , with a proper scaling for k in terms of n, has a convergent subsequence to exp(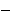 |k| |k|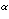   ) if d>2( ) if d>2(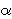 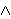 2). 2).
The key elements are the lace expansion for oriented percolation and a new bootstrapping argument to analyse the expansion coefficients for the long-range time-oriented model. |
|
| Laurent Saloff-Coste (Cornell University) | Wednesday 4th July 09:00 |
| Random walks on finitely generated groups I |
| This minicourse course will discuss random walks from the viewpoint of
the relations between the behavior of the processes and the (geometric
and algebraic) structure of the underlying group. In addition to results of a very general nature, many concrete examples will be discussed. |
|
| Laurent Saloff-Coste (Cornell University) | Saturday 7th July 10:00 |
| Random walks on finitely generated groups II |
|
|
| Laurent Saloff-Coste (Cornell University) | Monday 9th July 10:00 |
| Random walks on finitely generated groups III |
|
|
| Vladas Sidoravicius (Rio de Janeiro) | Friday 6th July 12:15 |
| Growth system with columnar defects and pinning problems |
|
|
| Gordon Slade (University of British Columbia) | Tuesday 3rd July 10:00 |
| Random walks and the lace expansion I |
The lace expansion has been developed since the mid-1980s into
a highly effective method to study the critical behaviour of
self-avoiding walks, percolation, and related models, usually in
high dimensions. The minicourse will provide an introduction to
the lace expansion with emphasis on two very recent applications
to random walks: the enumeration of self-avoiding walks,
and the analysis of random walk on the incipient infinite cluster
for oriented percolation.
Preprints for these lectures are available at http://www.math.ubc.ca/~slade
The first lecture will introduce the lace expansion for self-avoiding
walks and explain its recent use to count self-avoiding walks in
dimensions 3 and higher.
(Joint work with Nathan Clisby and Richard Liang.)
|
|
| Gordon Slade (University of British Columbia) | Wednesday 4th July 10:00 |
| Random walks and the lace expansion II |
(Joint work with Remco van der Hofstad and Frank den Hollander.)
The second lecture will discuss the application of the lace
expansion to study critical oriented percolation in spatial
dimensions above 4, including the construction of the incipient
infinite cluster.
|
|
| Gordon Slade (University of British Columbia) | Friday 6th July 09:00 |
| Random walks and the lace expansion III |
(Joint work with Martin Barlow, Antal Jarai, Takashi Kumagai.)
The third lecture will discuss recently proved estimates on the range,
exit times, and return probabilities of random walk on the incipient
infinite cluster for oriented percolation in dimensions above 6.
These estimates show that the spectral dimension of the incipient
infinite cluster is 4/3, and prove a version of the Alexander-Orbach
conjecture.
|
|
| Angela Stevens (University of Heidelberg) | Monday 9th July 16:45 |
| A PDE point of view on reinforced random walks |
| Formal ad hoc approximations of self-attracting reinforced random walks relate to systems of partial differential equations of chemotaxis type. These PDEs show a quite interesting behavior concerning existence of global solutions and finite time blow up, which depends on the spatial dimension and can formally be completely characterized. Rigorous results are work in progress.
Looking more carfully at suitable growth conditions for the reinforcements and by this trying to come closer to rigorous limiting descriptions, discrete models result. This talk explains and summarizes a larger research project undertaken together with J.J.L. Velazquez (Madrid). |
|
| Yurii Suhov (University of Cambridge) | Tuesday 10th July 17:15 |
| Anderson localisation for interacting particles |
| I'll discuss the joint result with Victor Chulaevsky (University
of Reims, Champagne-Ardennes) on localisation propertiers of the Anderson
tight binding model of several interacting particles. |
|
| Alain-Sol Sznitman (ETH Zurich) | Tuesday 3rd July 09:00 |
| Random walks and interfaces |
The general theme of this talk brings together random walks and percolation.
We present results related to the way paths of random walks can create interfaces.
We also discuss a model of "random interlacements" describing the microscopic
structure at hand. |
|
| Balint Toth (Technical University Budapest) | Friday 6th July 10:00 |
| Tagged particle diffusion in deterministic dynamics: old and new results |
| I will consider the M -> 0 limit for tagged particle diffusion in a 1-dimensional Rayleigh-gas, studied originaly by Sinai and Soloveichik (1986), respectively, by Szász and Tóth (1986). In this limit we derive a new type of model for tagged paricle diffusion, with Calogero-Moser (i.e. inverse quadratic) interaction potential between the two central particles. Computer simulations on this new model reproduce exactly the numerical value of the limiting variance obtained by Boldrighini, Frigio and Tognetti (2002). I will also present new bounds on the limiting variance of tagged particle diffusion in (variants of) 1D Rayleigh gas which improve some bounds of Szász, Tóth (1986). The talk will be based on joint work of the following three authors: Péter Bálint, Bálint Tóth, Péter Tóth. |
|
| Boris Tsirelson (Tel Aviv University) | Tuesday 10th July 12:15 |
| Random walks in semigroups: stability and sensitivity
|
| Sometimes a small fraction of factors has a dramatic impact on the product.
In the scaling limit it leads to unstable Brownian motions in semigroups.
It never happens in the commutative case.
|
|
| Rob van den Berg (CWI Amsterdam) | Friday 6th July 11:30 |
| Some standard and less standard coalescing random walk models |
| Will be provided soon |
|
| Remco van der Hofstad (Eindhoven) | Tuesday 3rd July 11:30 |
| An expansion for self-interacting random walks |
| Self-interacting random processes are receiving
tremendous attention in the past years. Examples
are reinforced random walks, true self-avoiding
walk, excited random walk, and loop-erased random
walk. Often, martingale techniques are used to
prove laws of large numbers and/or central limit
theorems. Unfortunately, the description of the
limiting parameters, for example the limiting drift,
is rather implicit, which makes it hard to investigate
its properties. For example, for many models it is
natural that the drift is monotone in a parameter
of the model.
In statistical mechanics, expansions such as the lace
expansion have proved a powerful tool to investigate
models with an interaction above the upper critical dimension.
We propose an expansion that applies in the general setting
of self-interacting random walks. In order to prove a LLN
and/or a CLT, apart from the expansion, one needs bounds
on the coefficients. We are able to prove these bounds in
two cases:
excited random walk above 8 dimensions and directed
once reinforced random walk, where the reference
random walk has a drift.
Interestingly, the drift is given explicitly in
terms of the expansion coefficients, which may
make it possible to prove monotonicity properties
of the drift.
This is joint work with Mark Holmes.
|
|
| Sasha Veretennikov (University of Leeds) | Wednesday 4th July 17:45 |
| On mixing for Markov diffusions and Poisson equations in Sobolev classes |
| Smoothness with respect to a parameter is established for Sobolev solutions of Poisson equations with ``ergodic'' generators |
|
| Stanislav Volkov (University of Bristol) | Friday 6th July 17:30 |
| Random walks with time and space dependent drifts |
| We consider a one-dimensional discrete-time stochastic process (walk) with asymptotically zero drift, which depends both on the time and the position of the walker. We establish an interesting phase transition
of these walks, which cover a range of models from Lamperti's problem
to Friedman's urn. For the latter, we manage to answer an apparently still open question.
|
|
| Jon Warren (University of Warwick) | Tuesday 3rd July 17:45 |
| Consistent families of Brownian motions |
| I will describe a martingale problem used to characterize multidimensional diffusions whose coordinates are each Brownian motions evolving independently of each other except when equal. Consistent familes of such diffusions arise in some generalizations of the Brownian web. |
|
| Matthias Winkel (University of Oxford) | Wednesday 4th July 17:15 |
| SLE and α-SLE driven by Levy processes |
| Stochastic Loewner Evolutions (SLE) with a multiple sqrt(κ) of Brownian motion B as driving process are random planar curves (if κ ≤ 4) or growing compact sets generated by a curve (if κ > 4). We consider here more general Levy processes as driving processes and obtain evolutions expected to look like random trees or compact sets generated by trees, respectively. We show that when the driving force is of the form sqrt(κ) B+θ(1/α) S for a symmetric α-stable Levy process S, the cluster has zero or positive Lebesgue measure according to whether κ ≤ 4 or κ > 4. We also give mathematical evidence that a further phase transition at α = 1 is attributable to the recurrence/transience dychotomy of the driving Levy process. We introduce a new class of evolutions that we call
α-SLE. They have α-self-similarity properties for α-stable Levy driving processes. We show the phase transition at a critical coefficient θ = θ0 |
|
| Wolfgang Woess (Graz University of Technology) | Thursday 5th July 12:15 |
| The Poisson boundary of lamplighter random walks on the homogeneous tree
|
(Joint work with Anders Karlsson, KTH, Stockholm)
Let F be a group which has the homogeneous tree as a Caley graph, and let L be a finite group (typically the two-element-group). The wreath product G of L with F is the "lamplighter group" over the tree. We study random walks on that group. In particular, we determine their Poisson boundary and study the solvability of the Dirichlet problem at infinity.
|
|
| Ofer Zeitouni (Univeristy of Minnesota) | Thursday 5th July 09:00 |
| Regeneration and quenched limits |
|


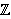
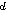
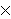
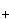 is a discrete-time analogue of the contact process, a model for the spread of an infection. Each time-oriented bond ((x,n),(y,n+1)) is either occupied with probability pD(y
is a discrete-time analogue of the contact process, a model for the spread of an infection. Each time-oriented bond ((x,n),(y,n+1)) is either occupied with probability pD(y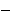 x) or vacant with probability 1
x) or vacant with probability 1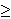 0 is the percolation parameter. We are interested in the random sets of vertices connected by occupied time-oriented bonds. It is known that the model exhibits a phase transition and critical behaviour around the phase transition point p=p
0 is the percolation parameter. We are interested in the random sets of vertices connected by occupied time-oriented bonds. It is known that the model exhibits a phase transition and critical behaviour around the phase transition point p=p .
.
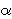 >0 and suppose that D(x) decays as |x|
>0 and suppose that D(x) decays as |x|
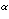 for large |x|. Let Z
for large |x|. Let Z (k;n) be the Fourier transform of
(k;n) be the Fourier transform of 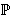
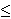 p
p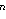 if d>2(
if d>2(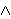 2), where m
2), where m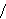 Z
Z
 ) if d>2(
) if d>2(