7 SL₃ 7.7 Weyl symmetry — not examinable 7.9 Proof of theorem 7.28 — nonexaminable

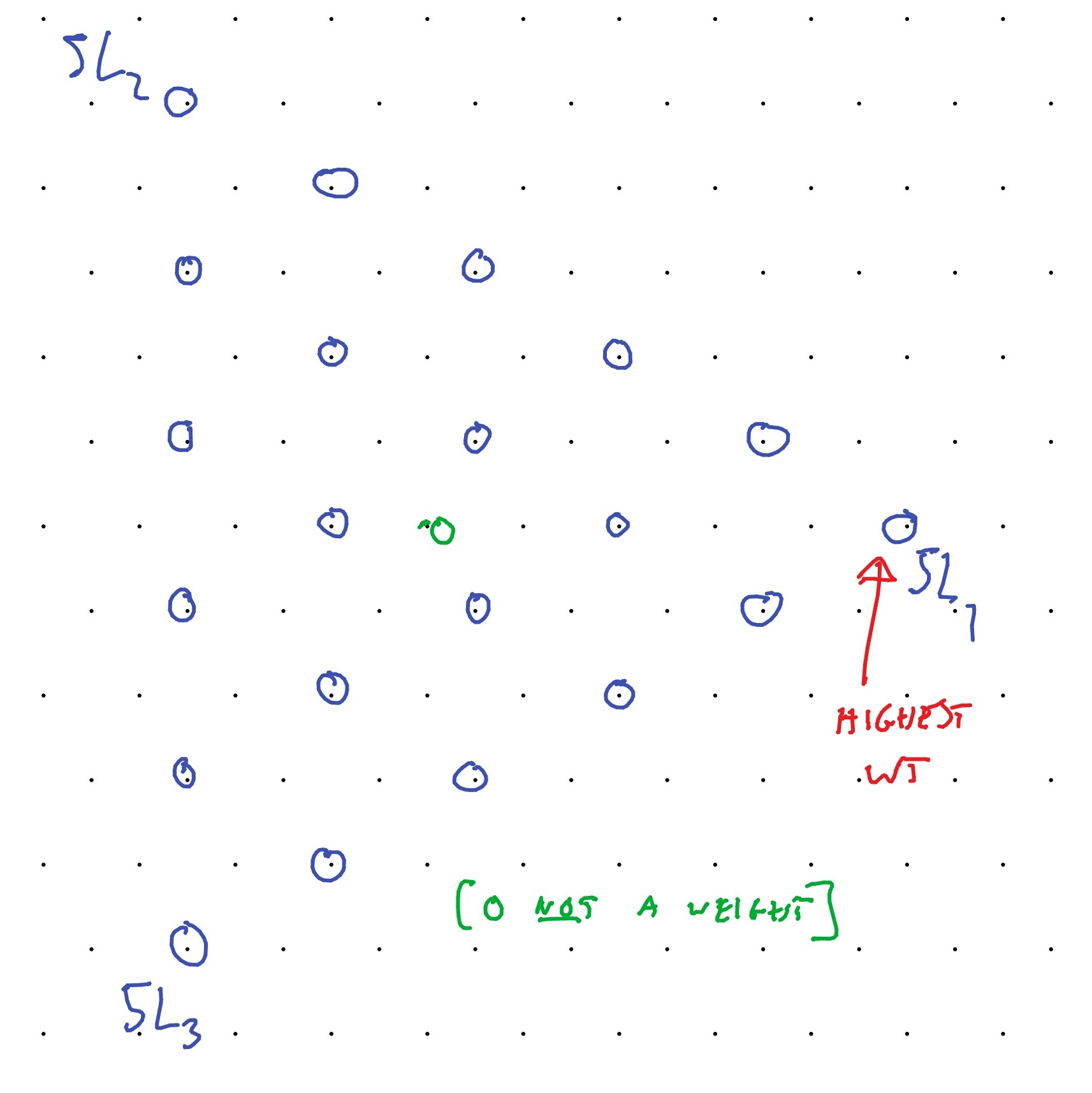
7.8 Irreducible representations of sl_3,C.

We are now in a position to state the main theorem of $\mathfrak{sl}_{3,\mathbb{C}}$ -theory.

Theorem 7.28.

For every pair $a, b$ of nonnegative integers, there is a unique (up to isomorphism) irreducible finite-dimensional representation $V^{(a,b)}$ of $\mathfrak{sl}_{3,\mathbb{C}}$ with a highest weight vector of weight $aL_{1}-bL_{3}$ .

Note that the highest weights occuring in the theorem are exactly the dominant elements of the weight lattice.

Since every irreducible finite-dimensional representation does have a highest weight, necessarily dominant, every irreducible representation is isomorphic to $V^{(a,b)}$ for some integers $a,b\geq 0$ .

Example 7.29.

We have already seen some examples:

1.

The standard representation $\mathbb{C}^{3}$ is irreducible with highest weight $L_{1}$ , therefore

$V^{(1,0)}=\mathbb{C}^{3}.$
2.

The dual to the standard representation is irreducible with highest weight $L_{3}$ , and so

$V^{(0,1)}=(\mathbb{C}^{3})^{*}.$
3.

The adjoint representation $\mathfrak{g}$ is irreducible with highest weight $L_{1}-L_{3}$ , and so

$V^{(1,1)}=\mathfrak{g}.$
4.

The symmetric square $\operatorname{Sym}^{2}(\mathbb{C}^{3})$ has highest weight $2L_{1}$ with highest weight vector $e_{1}^{2}$ .

Exercise 7.30.

(Problem 94). Show that, if $V$ is a finite-dimensional representation of $\mathfrak{sl}_{3,\mathbb{C}}$ with a unique highest weight vector (up to scalar), then $V$ is necessarily irreducible.

Deduce that the three representations listed above are indeed irreducible.

For a more general example, we have:

Exercise 7.31.

(Problem 96; non-examinable). Show that the representation $\operatorname{Sym}^{n}(\mathbb{C}^{3})$ has a unique highest weight vector with weight $nL_{1}$ . Deduce that

V^{(n,0)}=\operatorname{Sym}^{n}(\mathbb{C}^{3}).

Convince yourself that the weights in this case are as shown in Figure 13 (which illustrates the case $n=5$ ).

Figure 13: Weights for $\operatorname{Sym}^{n}(\mathbb{C}^{3})$ .

7.8 Irreducible representations of sl3,C.

Theorem 7.28.

Example 7.29.

Exercise 7.30.

Exercise 7.31.

7.8 Irreducible representations of sl_3,C.