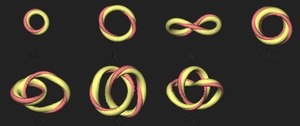Professor Paul Sutcliffe










Topological solitons are stable, finite energy, particle-like solutions
of nonlinear wave equations. They arise in a variety of applications
in several areas including particle physics, cosmology and
condensed matter physics.
Skyrmions are candidates for a solitonic description of nuclei, where
the number of solitons is identified with baryon number.
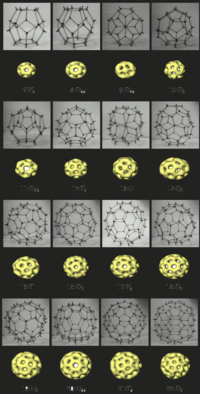
The Skyrme model solitons are only known through numerical computations.
However, it is possible to use an approximation in which Skyrmions are
constructed from rational maps between Riemann spheres, and this has
proved useful in understanding the structure of Skyrmions. The figure
displays baryon density isosurfaces for various soliton numbers plus
models to help visualize the associated polyhedra. It can be seen
that some Skyrmions are very symmetric, and this can be understood
in terms of the existence of particularly symmetric rational maps.
Monopoles arise in Yang-Mills-Higgs gauge theories and are solitons
that carry magnetic charge.
The equations describing
static BPS monopoles are integrable and this allows various sophisticated
twistor methods to be applied. Monopole dynamics is not an
integrable system but for slowly moving monopoles their dynamics can be
approximated by geodesic motion on the moduli space of static solutions.
The figure shows a particular scattering of three monopoles.
Monopoles often resemble Skyrmions and although this is not yet
completely understood there are some hints at a connection, as
monopoles can also be described by rational maps.
Solitons stabilized by the Hopf invariant (which is a linking number
between field lines) arise in the
Skyrme-Faddeev model. The figure shows two field lines for
each soliton with Hopf charge one to seven. It can be seen
that the first few solitons consist of a single loop, which in
some cases is twisted, but for higher Hopf charges links
and knots appear. The charge seven configuration is a trefoil knot and
many other links and knots appear with increasing Hopf charge.
Topological solitons
Below are some examples of 3D topological solitons.