Research overview
The probability group in Durham is actively involved in research in many areas of probability and its applications. Here are some of the main themes of our work.
Complex stochastic systems
Interactions among components of large systems often result in complex behaviour and new phenomena, such as phase transitions. Many of the phenomena can be successfully analysed with a probabilistic approach. We are interested in applications including random fields, percolation, random media, polymers, interacting particle systems, random tiling models, determinantal point processes, and other models inspired by statistical mechanics, biology, chemistry, and so on.
Stochastic processes and their applications
We study Markov processes, including random walks and branching processes, as well as non-Markov processes involving random environments or self-interactions. We have particular theoretical interest in explicit conditions for stability of near-critical stochastic systems. We work with both discrete and continuous models, and with the connections between them.
Random geometric, algebraic and combinatorial structures
We are interested in various probabilistic models for disordered structures or spatial systems, including random networks, random graphs or hypergraphs, and combinatorial structures constructed on random points in space, for example as solutions to certain optimization problems. The dependence inherent in such structures leads to interesting mathematical problems, and theoretical tools to handle such dependence are of interest.
Applications of probability
We work on applications to topics of interest in operations research, engineering, and risk analysis. These include queueing systems, communications networks, randomized algorithms, reliability networks, and decision making. We are also concerned with modelling and quantifying severe uncertainty, which arises in applications when there is insufficient data relative to model complexity, and when one is compelled to work with partial probability specifications such as probability bounds.
Postgraduate opportunities in probability
Postgraduate research in probability offers the opportunity to develop advanced mathematical expertise in your chosen area, as well as transferable skills including academic writing, presentation, and scientific computing. You will work on challenging and interesting mathematical problems, whose scope can include both pure mathematical research as well as bearing on real-world applications. A research degree offers excellent career prospects, in academia, industry, and the public sector.
For informal enquiries, please contact any member of the probability group. For practical information on applying, please contact the group's postgraduate admissions officer.
Funding opportunities are listed here.
The probability group has regular seminars, and regular regional events include Probability in the North East PiNE and the RSS North East local group seminars.
Possible topics for postgraduate research
We would be very interested in supervising postgraduate research on any topic that fits well with our research interests. Here are a few descriptions of specific potential topic areas: this list is far from exhaustive.
The two-periodic Aztec diamond and related models
Contact: Sunil Chhita

Spin systems
Contact: Tyler Helmuth
Branching Brownian motion with killing
Contact: Ellen Powell
Conformal welding and Liouville quantum gravity
Contact: Ellen Powell
Random growth models
Contact: Mustazee Rahman
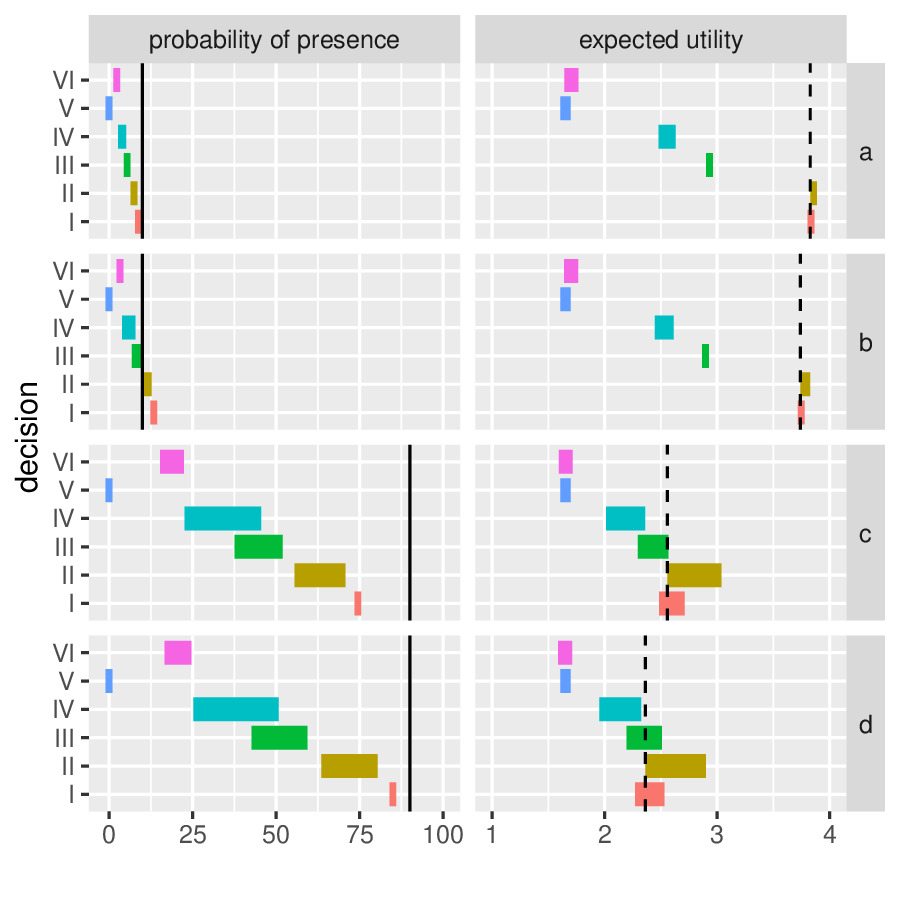
Probability bounding to support decision making under severe uncertainty
Contact: Matthias Troffaes
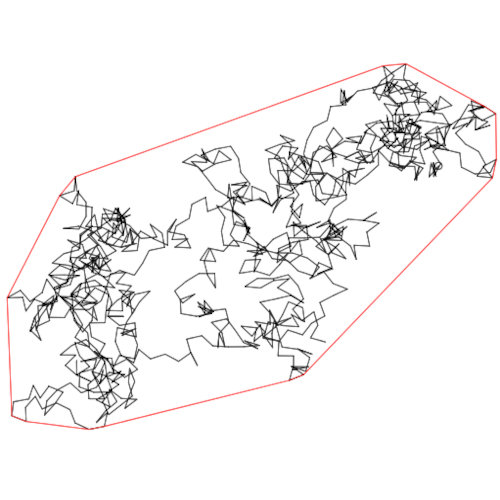
Convex hulls of stochastic processes
Contact: Andrew Wade
Geometric and stochastic analysis of interacting particle systems
Contact: Kohei Suzuki
