Topic 2 - Complex Numbers

Week 4 Material

Question 2.1 $\;$ If $z_1=2+3i$ and $z_2=-1+i$, find the real and imaginary parts of

$\;\;(a)\;\;z_1+z_2,\hspace{1cm}$ $(b)\;\;z_1-z_2,\hspace{1cm}$ $(c)\;\;z_1z_2,\hspace{1cm}$ $(d)\;\;z_1/z_2,$

$\;\;(e)\;\;\overline{z_1}z_2,\hspace{1.5cm}$ $(f)\;\;z_1\overline{z_2},\hspace{1.5cm}$ $(g)\;\;z_1\overline{z_1},\hspace{1.cm}$ $(h)\;\;z_2\overline{z_2}$.

Quick Check

$(a)\;\;$ $\Re(z_1+z_2)=1\quad\text{and}\quad \Im(z_1+z_2)=4.$

$(b)\;\;$ $\Re(z_1-z_2)=3\quad\text{and}\quad\Im(z_1+z_2)=2.$

$(c)\;\;$ $\Re(z_1z_2)=-5\quad\text{and}\quad\Im(z_1z_2)=-1.$

$(d)\;\;$ $\Re(z_1/z_2)=1/2\quad\text{and}\quad\Im(z_1/z_2)=-5/2.$

$(e)\;\;$ $\Re(\overline{z_1}z_2)=1\quad\text{and}\quad\Im(\overline{z_1}z_2)=5.$

$(f)\;\;$ $\Re(z_1\overline{z_2})=1\quad\text{and}\quad\Im(z_1\overline{z_2})=-5.$

$(g)\;\;$ $\Re(z_1\overline{z_1})=13\quad\text{and}\quad\Im(z_1\overline{z_1})=0.$

$(h)\;\;$ $\Re(z_2\overline{z_2})=2\quad\text{and}\quad\Im(z_2\overline{z_2})=0.$

Solution

For these, it is fine to leave the answers in the form $a+ib$ where $a,b\in\mathbb{R}$. However, be warned, you should answer the question that is asked!

$(a)\;\;$ We have $\;z_1+z_2=(2+3i)+(-1+i)=1+4i\;$ so \[\Re(z_1+z_2)=1\quad\text{and}\quad\Im(z_1+z_2)=4.\] $(b)\;\;$ We have $\;z_1-z_2=(2+3i)-(-1+i)=3+2i\;$ so \[\Re(z_1-z_2)=3\quad\text{and}\quad\Im(z_1+z_2)=2.\] $(c)\;\;$ We have $\;z_1z_2=(2+3i)(-1+i)=-2-3i+2i+3i^2=-5-i\;$ so \[\Re(z_1z_2)=-5\quad\text{and}\quad\Im(z_1z_2)=-1.\] $(d)\;\;$ We have $\dfrac{z_1}{z_2}=\dfrac{(2+3i)(-1-i)}{(-1+i)(-1-i)} =\dfrac{-2-3i-2i-3i^2}{1-i+i-i^2}=\dfrac{1-5i}{2}\;$ so \[\Re(z_1/z_2)=\dfrac12\quad\text{and}\quad\Im(z_1/z_2)=-\dfrac52.\] $(e)\;\;$ We have $\;\overline{z_1}z_2=(2-3i)(-1+i)=-2+3i+2i-3i^2=1+5i\;$ so \[\Re(\overline{z_1}z_2)=1\quad\text{and}\quad\Im(\overline{z_1}z_2)=5.\] $(f)\;\;$ We have $\;z_1\overline{z_2}=(2+3i)(-1-i)=-2-3i-2i-3i^2=1-5i\;$ so \[\Re(z_1\overline{z_2})=1\quad\text{and}\quad\Im(z_1\overline{z_2})=-5.\] (Alternatively, this is just the conjugate of the previous question.)

$(g)\;\;$ We have $\;z_1\overline{z_1}=(2+3i)(2-3i)=2^2+6i-6i-3^2i^2=4^2+3^2=13\;$ so \[\Re(z_1\overline{z_1})=13\quad\text{and}\quad\Im(z_1\overline{z_1})=0.\] (Alternatively, this is just $|z_1|^2$.)

$(h)\;\;$ We have $\;z_2\overline{z_2}=(-1+i)(-1-i)=(-1)^2+i-i-i^2=(-1)^2+1^2=2\;$ so \[\Re(z_2\overline{z_2})=2\quad\text{and}\quad\Im(z_2\overline{z_2})=0.\] (Alternatively, this is just $|z_2|^2$.)

Question 2.2 $\!{}^*\;$ Find the real and imaginary parts of

$\;\;(a)\;\;\dfrac{2+5i}{3+2i},\hspace{1cm}$ $(b)\;\;\dfrac{1}{i^7},\hspace{1cm}$ $(c)\;\;\left(-\dfrac{1}{2}+i\dfrac{\sqrt{3}}{2}\right)^2,\hspace{1cm}$ $(d)\;\;\left(-\dfrac{1}{2}+i\dfrac{\sqrt{3}}{2}\right)^{33}.$

Quick Check

$(a)\;$ The real part is $16/13$ and the imaginary part is $11/13$.

$(b)\;$ The real part is $0$ and the imaginary part is $1$.

$(c)\;$ The real part is $-1/2$ and the imaginary part is $-\sqrt{3}/2$.

$(d)\;$ The real part is $1$ and the imaginary part $0$.

Solution

Tutorial question

$(a)\;$ We have \[\dfrac{2+5i}{3+2i}=\dfrac{2+5i}{3+2i}\cdot\dfrac{3-2i}{3-2i} =\dfrac{6-4i-15i-10i^2}{9-6i+6i-4i^2}=\dfrac{16+11i}{13}\] so the real part is $\dfrac{16}{13}$ and the imaginary part is $\dfrac{11}{13}$.

$(b)\;$ There are various ways to do this, e.g. \[\frac{1}{i^7}=\frac{1}{(i^2)^3i} =\frac{1}{-i}=\frac{1}{-i}\left(\frac{i}{i}\right)=i\] or just notice $i^7i=i^8=(-1)^4=1$. However you do it, the real part is $0$ and the imaginary part is $1$.

$(c)\;$ We have $\left(-\dfrac{1}{2}+i\dfrac{\sqrt{3}}{2}\right)^2= \dfrac14-i\dfrac{\sqrt{3}}{4}-i\dfrac{\sqrt{3}}{4}+i^2\dfrac{3}{4} =-\dfrac{1}{2}-i\dfrac{\sqrt{3}}{2}$

so the real part is $-\dfrac{1}{2}$ and the imaginary part is $-\dfrac{\sqrt{3}}{2}$.

$(d)\;$ It’s probably a bad idea to expand the 33rd power of $z=-\dfrac{1}{2}+i\dfrac{\sqrt{3}}{2}$ directly!

Instead, using part $(c)$ we have \[z^3=\left(-\dfrac{1}{2}+i\dfrac{\sqrt{3}}{2}\right)^{3}= \left(-\dfrac{1}{2}+i\dfrac{\sqrt{3}}{2}\right) \left(-\dfrac{1}{2}-i\dfrac{\sqrt{3}}{2}\right)= \dfrac14-i\dfrac{\sqrt{3}}{4}+i\dfrac{\sqrt{3}}{4}-i^2\dfrac{3}{4}=1 \] Hence $z^{33}=1^{11}=1$ which has real part 1 and imaginary part 0.

Alternatively, notice $|z|=1$ and $\arg(z)=2\pi/3$ so $z^{33}=1$ since \[|z^{33}|=|z|^{33}=1\qquad\text{and}\qquad \arg(z^{33})=33\arg(z)=22\pi\quad\text{i.e. $\arg(z^{33})=0$}.\]

Question 2.3 $\;$ Suppose $z=x+iy$ where $x$ and $y$ are real. Express each of the following in terms of $x$ and $y$.

$\;\;(a)\;\;\Re(z^3),\hspace{1cm}$ $(b)\;\;\Im(z^3),\hspace{1cm}$ $(c)\;\;\Re\left(1/\overline{z}\right),\hspace{1cm}$ $(d)\;\;\Im(z+z^{-1}).$

Quick Check

$(a)\;$ $\;\Re(z^3)=x^3-3xy^2$. $\hspace{1cm}$ $(b)\;$ $\;\Im(z^3)=3x^2y-y^3$.

$(c)\;$ $\;\Re\left(1/\overline{z}\right)=\dfrac{x}{x^2+y^2}$. $\hspace{1cm}$ $(d)\;$ $\;\Im(z+z^{-1})=y-\dfrac{y}{x^2+y^2}$.

Solution

$(a)\;$ We have \[z^3=(x+iy)^3=x^3+3ix^2y+3xi^2y^2+i^3y^3=(x^3-3xy^2)+i(3x^2y-y^3)\] and taking real parts gives $\;\Re(z^3)=x^3-3xy^2$.

$(b)\;$ Similarly, taking imaginary parts gives $\;\Im(z^3)=3x^2y-y^3$.

$(c)\;$ \[\frac{1}{\overline{z}}=\frac{1}{x-iy}=\frac{x+iy}{(x-iy)(x+iy)}= \frac{x}{x^2+y^2}+i\frac{y}{x^2+y^2}\] which implies $\;\Re\left(1/\overline{z}\right)=\dfrac{x}{x^2+y^2}$.

$(d)\;$ \[z+z^{-1}=x+iy+\frac{1}{x+iy}=x+iy+\frac{x-iy}{x^2+y^2}\] which implies $\;\Im(z+z^{-1})=y-\dfrac{y}{x^2+y^2}$.

Question 2.4 $\;$ Calculate the modulus and principal argument of each of the following complex numbers:

$\;\;(a)\;\;1+\sqrt{3}i,\hspace{2.2cm}$ $(b)\;\;3+2i,\hspace{3cm}$ $(c)\;\;-6i,$

$\;\;(d)\;\;\dfrac{2+i}{3-i}-\dfrac{4+i}{1+2i},\hspace{1cm}$ $(e)\;\;\dfrac{2+3i}{i}+\dfrac{5+10i}{2+i},\hspace{1cm}$ $(f)\;\;\dfrac{3+2i}{1+i}+\dfrac{5-2i}{-1+i}.$

Quick Check

$(a)\;$ $|1+\sqrt{3}i|=2$, $\Arg(1+\sqrt{3}i)=\dfrac{\pi}{3}$.

$(b)\;$ $|3+2i|=\sqrt{13}$, $\Arg(3+2i)=\arctan\left(\dfrac23\right)$.

$(c)\;$ $|-6i|=6$, $\Arg(-6i)=-\dfrac{\pi}{2}$.

$(d)\;$ $|z|=\sqrt{4.1}$, $\Arg(z)=\pi-\arctan\left(\dfrac{19}{7}\right)$.

$(e)\;$ $|z|=\sqrt{50}$, $\Arg(z)=\arctan\left(\dfrac{1}{7}\right)$.

$(f)\;$ $|z|=\sqrt{5}$, $\Arg(z)=\arctan(2)-\pi$.

Solution

$(a)\;$

The modulus is $|1+\sqrt{3}i|=\sqrt{1^2+\left(\sqrt{3}\right)^2}=2$.

Also, $1+\sqrt{3}i$ is in the upper right quadrant so $\Arg(1+\sqrt{3}i)=\arctan\left(\dfrac{\sqrt{3}}{1}\right)=\dfrac{\pi}{6}$.

$(b)\;$

The modulus is $|3+2i|=\sqrt{3^2+2^2}=\sqrt{13}$.

Also, $3+2i$ is in the upper right quadrant so $\Arg(3+2i)=\arctan\left(\dfrac23\right)$.

$(c)\;$

The modulus is $|-6i|=\sqrt{0^2+(-6)^2}=6$. Also, from the diagram, $\Arg(-6i)=-\dfrac{\pi}{2}$.

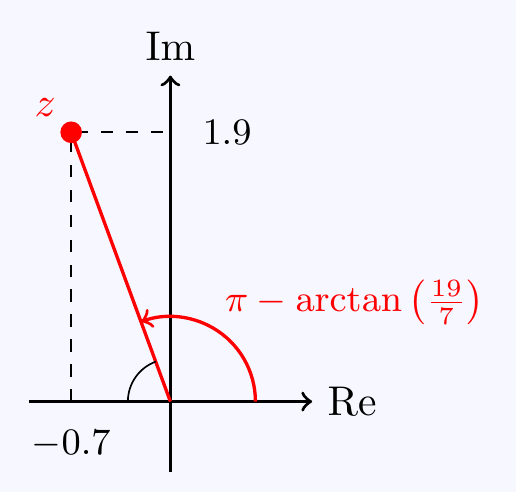
$(d)\;$ First calculate $z=\dfrac{2+i}{3-i}-\dfrac{4+i}{1+2i}=\dfrac{5+5i}{10}-\dfrac{6-7i}{5}=-0.7+1.9i$.

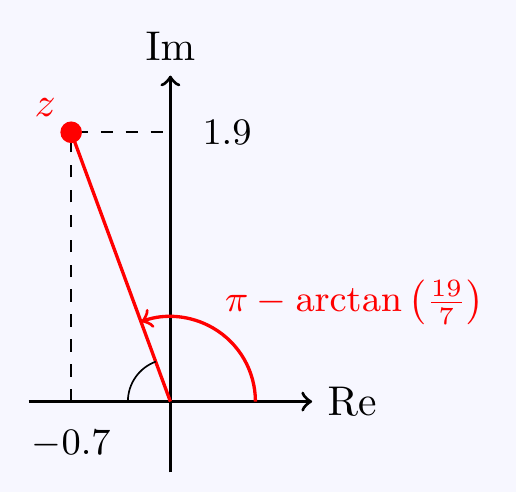
Then $|z|=\sqrt{0.7^2+1.9^2}=\sqrt{4.1}$. Also, from the diagram, $\Arg(z)=\pi-\arctan\left(\dfrac{19}{7}\right)$.

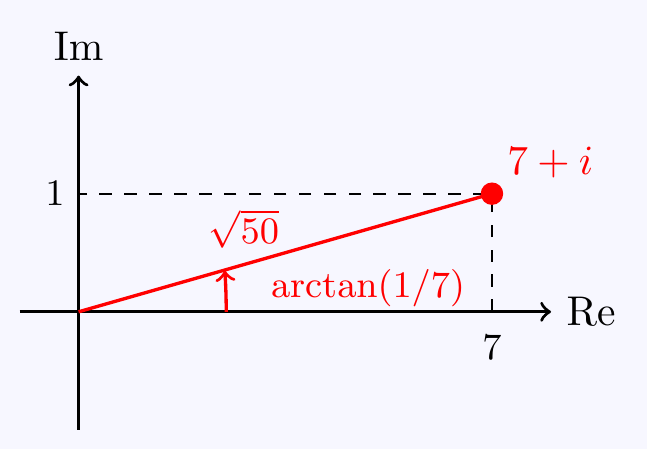
$(e)\;$ First calculate $z=\dfrac{2+3i}{i}-\dfrac{5+10i}{2+i}=\dfrac{5+5i}{10}-\dfrac{6+7i}{5}=7+i$.

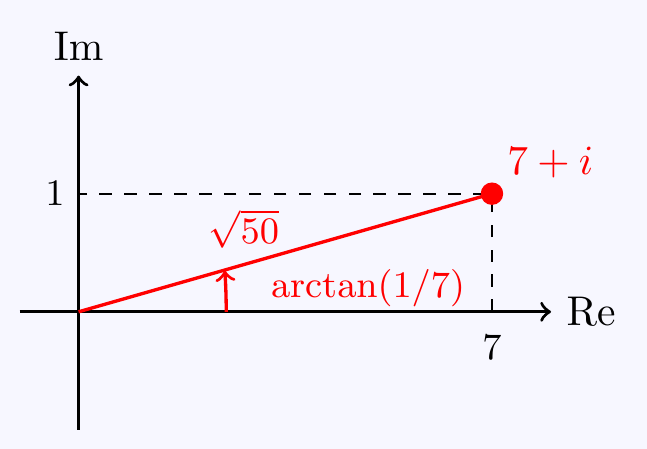
Then $|z|=\sqrt{7^2+1^2}=\sqrt{50}$. Also, from the diagram, $\Arg(z)=\arctan\left(\dfrac{1}{7}\right)$.

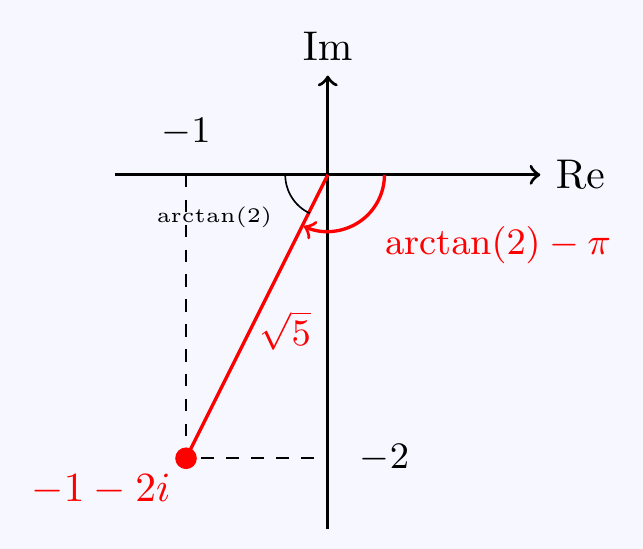
$(f)\;$ First calculate $z=\dfrac{3+2i}{1+i}+\dfrac{5-2i}{-1+i}$ $=\dfrac{5-2i}{2}+\dfrac{-7+3i}{2}=-1-2i$.

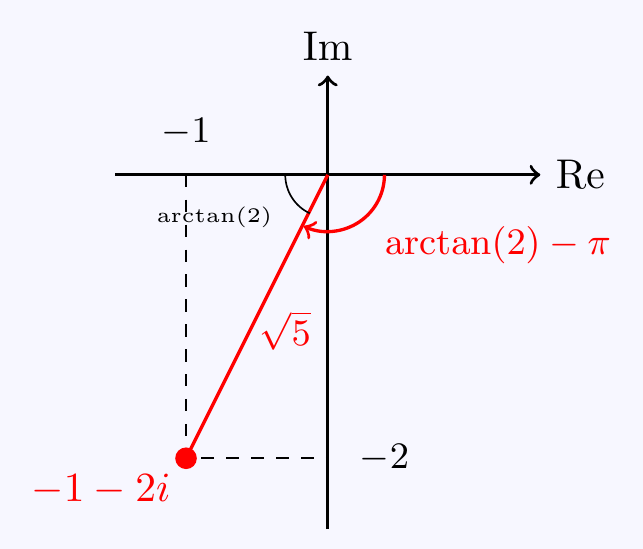
Then $|z|=\sqrt{1^2+2^2}=\sqrt{5}$. Also, from the diagram, $\Arg(z)=\arctan(2)-\pi$.

Question 2.5 $\;$ If $z_1=1+i\sqrt{3}$ and $z_2=2+2i$, find the modulus and principal argument of

$\;\;(a)^*\;\;z_1,\hspace{1.5cm}$ $(b)^*\;\;z_2,\hspace{1.5cm}$ $(c)\;\;\overline{z_1},\hspace{1.5cm}$ $(d)\;\;\overline{z_2},$

$\;\;(e)\;\;z_1z_2,\hspace{1cm}$ $(f)^*\;\;z_1/z_2,\hspace{1cm}$ $(g)\;\;z_2/z_1,\hspace{1cm}$ $(h)^*\;\;z_1+z_2.$

Quick Check

$(a)\;$ Tutorial question

$(b)\;$ Tutorial question

$(c)\;$ $\displaystyle |\overline{z_1}|=2\qquad\text{and}\qquad \Arg(\overline{z_1})=-\frac{\pi}{3}.$

$(d)\;$ $\displaystyle |\overline{z_2}|=2\sqrt{2}\qquad\text{and}\qquad \Arg(\overline{z_2})=-\frac{\pi}{4}.$

$(e)\;$ $\displaystyle |z_1z_2|=4\sqrt{2}\qquad\text{and}\qquad \Arg(z_1z_2)=\frac{7\pi}{12}.$

$(f)\;$ Tutorial question

$(g)\;$ $\displaystyle \left|\frac{z_2}{z_1}\right|=\sqrt{2}\qquad\text{and}\qquad \Arg\left(\frac{z_2}{z_1}\right)=-\frac{\pi}{12}.$

$(h)\;$ Tutorial question

Solution

Remember that the “formula” $\arctan(y/x)$ doesn’t always give the correct angle - it may be out by $\pm\pi.$ Also, remember the principal argument must be in the range $-\pi<\theta\leq\pi$. If in doubt, draw a picture!

$(a)\;$ Tutorial question

$\displaystyle |z_1|=\sqrt{1^2+(\sqrt{3})^2}=2\qquad\text{and}\qquad \Arg(z_1)=\arctan\sqrt{3}=\frac{\pi}{3}.$

$(b)\;$ Tutorial question

$\displaystyle |z_2|=\sqrt{2^2+2^2}=2\sqrt{2}\qquad\text{and}\qquad \Arg(z_2)=\arctan\frac{\sqrt{2}}{2}=\frac{\pi}{4}.$

$(c)\;$ $\displaystyle |\overline{z_1}|=|z_1|=2\qquad\text{and}\qquad \Arg(\overline{z_1})=-\Arg(z_1)=-\frac{\pi}{3}.$

$(d)\;$ $\displaystyle |\overline{z_2}|=|z_2|=2\sqrt{2}\qquad\text{and}\qquad \Arg(\overline{z_2})=-\Arg(z_2)=-\frac{\pi}{4}.$

$(e)\;$ $\displaystyle |z_1z_2|=|z_1||z_2|=4\sqrt{2}\qquad\text{and}\qquad \Arg(z_1z_2)=\Arg(z_1)+\Arg(z_2)=\frac{7\pi}{12}.$

$(f)\;$ Tutorial question

$\displaystyle \left|\frac{z_1}{z_2}\right|=\frac{|z_1|}{|z_2|}=\frac{\sqrt{2}}{2}\qquad\text{and}\qquad \Arg\left(\frac{z_1}{z_2}\right)=\Arg(z_1)-\Arg(z_2)=\frac{\pi}{12}.$

$(g)\;$ $\displaystyle \left|\frac{z_2}{z_1}\right|=\frac{|z_2|}{|z_1|}=\sqrt{2}\qquad\text{and}\qquad \Arg\left(\frac{z_2}{z_1}\right)=\Arg(z_2)-\Arg(z_1)=-\frac{\pi}{12}.$

$(h)\;$ Tutorial question

We have $z_1+z_2=3+i(2+\sqrt{3})$ so \[|z_1+z_2|=\sqrt{3^2+(2+\sqrt{3})^2}=2\sqrt{4+\sqrt{3}}\qquad\text{and}\qquad \Arg(z_1+z_2)=\arctan\left(\frac{2+\sqrt{3}}{3}\right).\]

Question 2.6 $\!{}^*\;$ Which of the following are true for all complex numbers $z$ and $w$? In each case, either prove it is true or give a counterexample.

$\;\;(a)\;\;\Re(z+w)=\Re(z)+\Re(w),\hspace{1.5cm}$ $(b)\;\;\Re(zw)=\Re(z)\Re(w),$

$\;\;(c)\;\;|z+w|=|z|+|w|,\hspace{3.3cm}$ $(d)\;\;\arg(z+w)=\arg(z)+\arg(w).$

Quick Check

$(a)\;$ True. $\hspace{1cm}$ $(b)\;$ False. $\hspace{1cm}$ $(c)\;$ False. $\hspace{1cm}$ $(d)\;$ False.

Solution

Tutorial question

$(a)\;$ This is true: for $z=x+iy$, $w=u+iv$ we have \[\Re(z+w)=\Re\left(x+u+i(y+v)\right)=x+u=\Re(z)+\Re(w).\]

$(b)\;$ This is false: e.g. for $z=i$, $w=i$ we have \[\Re(zw)=\Re(-1)=-1\qquad\text{but}\qquad\Re(i)\Re(i)=0\cdot 0 =0.\]

$(c)\;$ This is false: e.g. for $z=1$, $w=i$, \[|z+w|=\sqrt{1^2+1^2}=\sqrt{2}\qquad\text{but}\qquad |z|+|w|=1+1=2.\]

$(d)\;$ This is false: e.g. for $z=1$, $w=i$, \[\arg(z+w)=\arg(1+i)=\frac{\pi}{4} \qquad\text{but}\qquad \arg(z)+\arg(w)=0+\frac{\pi}{2}=\frac{\pi}{2}.\]

Question 2.7 $\;$ Suppose $a$, $b$ and $c$ are real numbers with $b^2<4ac$ and $z$ is a complex number satisfying \[az^2+bz+c=0.\] Find $|z|^2=z\overline{z}$ in terms of $a$, $b$ and $c$.

Quick Check

Hint: Use the quadratic formula to find $z$ and show that $z\overline{z}=c/a.$

Solution

The quadratic has two complex conjugate roots \[z,\overline{z}=\frac{-b\pm\sqrt{b^2-4ac}}{2a}=-\frac{b}{2a}\pm i\frac{\sqrt{4ac-b^2}}{2a}\] (Notice $4ac-b^2>0$ so its square root is real.) Hence \[z\overline{z}=|z|^2=\left(-\frac{b}{2a}\right)^2+\left(\frac{\sqrt{4ac-b^2}}{2a}\right)^2 =\frac{b^2+4ac-b^2}{4a^2}=\frac{c}{a}.\]

Question 2.8 $\;$ Find the modulus and argument of $1+i$ and hence find the real and imaginary parts of $(1+i)^{10}$.

Quick Check

Find $|1+i|=\sqrt2,\;\;\arg(1+i)=\pi/4$ and $\Re((1+i)^{10})=0,\;\;\Im((1+i)^{10})=32$.

Solution

We have $|1+i|=\sqrt{1^2+1^2}=\sqrt2$ and $\arg(1+i)=\arctan(1/1)=\pi/4$ so $1+i=\sqrt2e^{\pi i/4}$. Hence \[(1+i)^{10}=\left(\sqrt2e^{\pi i/4}\right)^{10}=2^5e^{\frac{10\pi}{4}i} =32e^{\frac{\pi}{2}i}=32\left(\cos\frac{\pi}{2}+i\sin\frac{\pi}{2}\right)=32i\] which has real part $0$ and imaginary part $32$.

Week 5 Material

Question 2.9 $\;$ Find all possible values of

$\;\;(a)\;\; i^0, \hspace{1cm}$ $\;\;(b)\;\; i^1, \hspace{1cm}$ $\;\;(c)\;\; i^i, \hspace{1cm}$ $\;\;(d)\;\; (1+i)^i, \hspace{1cm}$ $\;\;(e)^*\;\; (1+i)^{2+i}.$

Quick Check

$(a)\;$ $i^0=1$. $\hspace{1cm}$ $(b)\;$ $i^1=i$.

$(c)\;$ $i^i=e^{-\pi/2-2n\pi} \quad\;\;$ for any $n\in\mathbb{Z}$.

$(d)\;$ $(1+i)^i=e^{-\pi/4-2n\pi+i\ln\sqrt{2}} \quad\;\;$ for any $n\in\mathbb{Z}$.

$(e)\;$ $(1+i)^{2+i}=2e^{-\pi/4-2n\pi}e^{(\ln{2}+\pi)i/2} \quad\;\;$ for any $n\in\mathbb{Z}$.

Solution

$(a)\;$ We have $z^0=1$ for any $z\neq 0$. So $i^0=1$.

$(b)\;$ It should be clear that $i^1=i$.

$(c)\;$ In polar form, $i=e^{\pi i/2}=e^{\pi i/2+2n\pi i}$ for any $n\in\mathbb{Z}$. So \[\begin{align*} i^i=\left(e^{\pi i/2+2n\pi i}\right)^i &=e^{\left(\pi i/2+2n\pi i\right)i}\\ &=e^{-\pi/2-2n\pi} \end{align*}\] $\quad\;\;$ for any $n\in\mathbb{Z}$.

$(d)\;$ In polar form, $1+i=\sqrt{2}e^{\pi i/4}=e^{\ln\sqrt{2}+\pi i/4+2n\pi i}$ for any $n\in\mathbb{Z}$. So \[\begin{align*} (1+i)^i=\left(e^{\ln\sqrt{2}+\pi i/4+2n\pi i}\right)^i &=e^{\left(\ln\sqrt{2}+\pi i/4+2n\pi i\right)i} \\ &=e^{\pi/4-2n\pi+i\ln\sqrt{2}} \end{align*}\] $\quad\;\;$ for any $n\in\mathbb{Z}$.

$(e)\;$ Tutorial question

In polar form, $1+i=\sqrt{2}e^{\pi i/4}=e^{\ln\sqrt{2}+\pi i/4+2n\pi i}$ for any $n\in\mathbb{Z}$. So \[\begin{align*} (1+i)^{2+i}&=\left(e^{\ln\sqrt{2}+\pi i/4+2n\pi i}\right)^{2+i} =e^{\left(\ln\sqrt{2}+\pi i/4+2n\pi i\right)(2+i)} \\ &=e^{2\ln\sqrt{2}-\pi/4-2n\pi+i\left(\ln\sqrt{2}+\pi/2+4n\pi\right)}\\ &=2e^{-\pi/4-2n\pi}e^{(\ln{2}+\pi)i/2} \end{align*}\] $\quad\;\;$ for any $n\in\mathbb{Z}$.

Question 2.10 $\;$ For each of the following equations, find all complex solutions and plot them on the complex plane.

$\;\;(a)\;\; z^5-32=0, \hspace{1.7cm}$ $\;\;(b)\;\; z^5+32=0, \hspace{1.0cm}$ $\;\;(c)\;\; z^6+8i=0, \hspace{1cm}$

$\;\;(d)\;\; z^2+2z+2=0, \hspace{1cm}$ $\;\;(e)^*\;\; z^6-9z^3+8=0.$

Quick Check

$(a)\;$ $z=2e^{2n\pi i/5}=2\left(\cos\dfrac{2n\pi}{5}+i\sin\dfrac{2n\pi}{5}\right)$ for $n=-2,-1,0,1,2$.

$(b)\;$ $z=2e^{(2n+1)\pi i/5}= 2\left(\cos\dfrac{(2n+1)\pi}{5}+i\sin\dfrac{(2n+1)\pi}{5}\right)$ for $n=-2,-1,0,1,2$.

$(c)\;$ $z=\sqrt{2}e^{(4n-1)\pi i/12}= \sqrt2\left(\cos\dfrac{(4n-1)\pi}{12}+i\sin\dfrac{(4n-1)\pi}{12}\right)$ for $n=-2,-1,0,1,2$.

$(d)\;$ $z=-1\pm i$

$(e)\;$ $z=e^{2n\pi i/3}, \;2e^{2n\pi i/3} \qquad\text{for $n=-1,0,1$.}$ These six solutions can also be written as \[1,\;\dfrac{-1\pm i\sqrt3}{2}\quad\textrm{and} 2,\; -1\pm i\sqrt3.\]

Solution

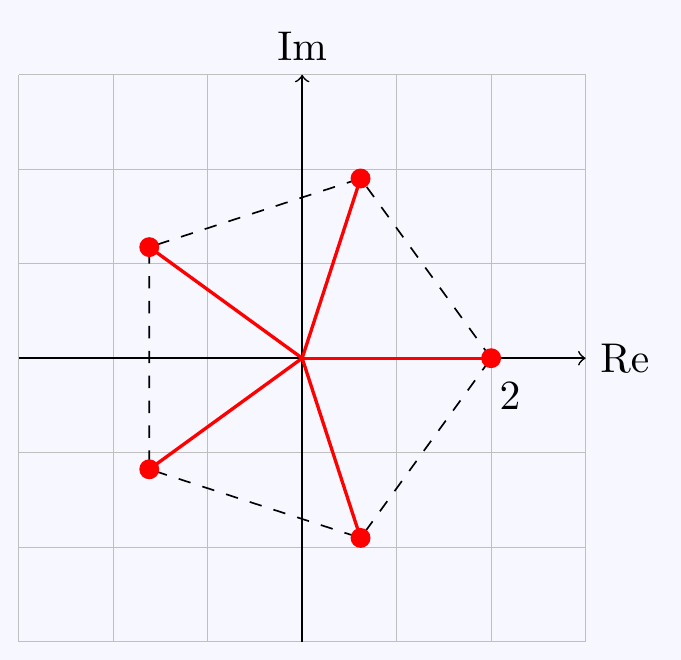
$(a)\;$ Write in polar form using $z=re^{i\theta}$ and $32=32e^{2n\pi i}$. Then \[\begin{align*} r^5e^{5i\theta}=32e^{2n\pi i} &\qquad\iff\qquad \begin{cases} r^5&=32 \\ 5\theta &=2n\pi \end{cases}\\ &\qquad\iff\qquad \begin{cases} r&=2 \\ \theta &=\frac{2n\pi}{5} \end{cases} \end{align*}\] The solutions are \[z=2e^{2n\pi i/5}=2\left(\cos\dfrac{2n\pi}{5}+i\sin\dfrac{2n\pi}{5}\right)\] for $n=0,1,2,3,4$. These sit at the vertices of a regular pentagon.

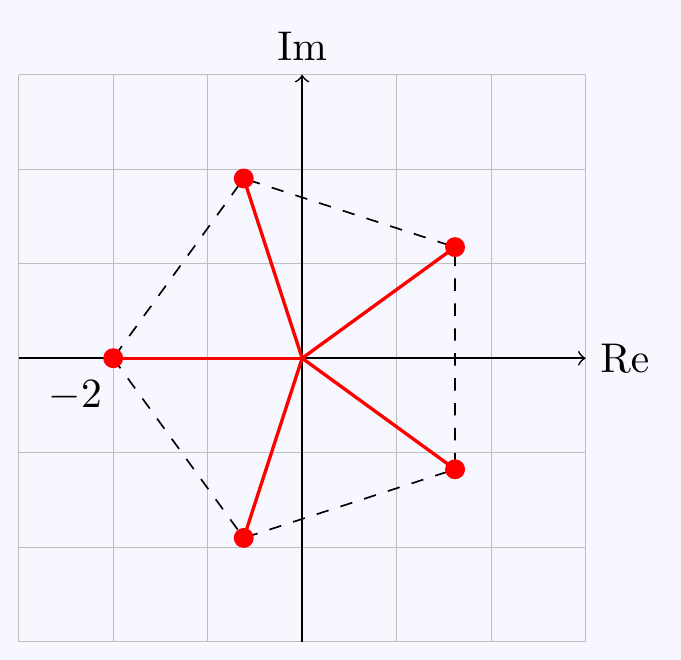
$(b)\;$ Write in polar form using $z=re^{i\theta}$ and $-32=32e^{\pi i + 2n\pi i}$. Then \[\begin{align*} r^5e^{5i\theta}=32e^{(2n+1)\pi i} &\qquad\iff\qquad \begin{cases} r^5&=32 \\ 5\theta &=(2n+1)\pi i \end{cases} \\ &\qquad\iff\qquad \begin{cases} r&=2 \\ \theta &=\frac{(2n+1)\pi}{5} \end{cases} \end{align*}\] The solutions are \[z=2e^{(2n+1)\pi i/5}= 2\left(\cos\dfrac{(2n+1)\pi}{5}+i\sin\dfrac{(2n+1)\pi}{5}\right)\] for $n=0,1,2,3,4$. As in the last question, these sit at the vertices of a regular pentagon.

$(c)\;$ Write in polar form using $z=re^{i\theta}$ and $-8i=8e^{-\pi i/2 + 2n\pi i}$. Then \[r^6e^{6i\theta}=8e^{(2n-\frac12)\pi i} \quad\iff\quad \begin{cases} r^6\!\!\!&=8 \\ 6\theta\!\!\!&=(2n-\frac12)\pi i \end{cases} \quad\iff\quad \begin{cases} r\!\!\!&=\sqrt{2} \\ \theta\!\!\!&=\dfrac{(4n-1)\pi}{12} \end{cases}\] The solutions are \[z=\sqrt{2}e^{(4n-1)\pi i/12}= \sqrt2\left(\cos\dfrac{(4n-1)\pi}{12}+i\sin\dfrac{(4n-1)\pi}{12}\right)\] for $n=0,1,2,3,4,5$. This time the solutions form a regular hexagon

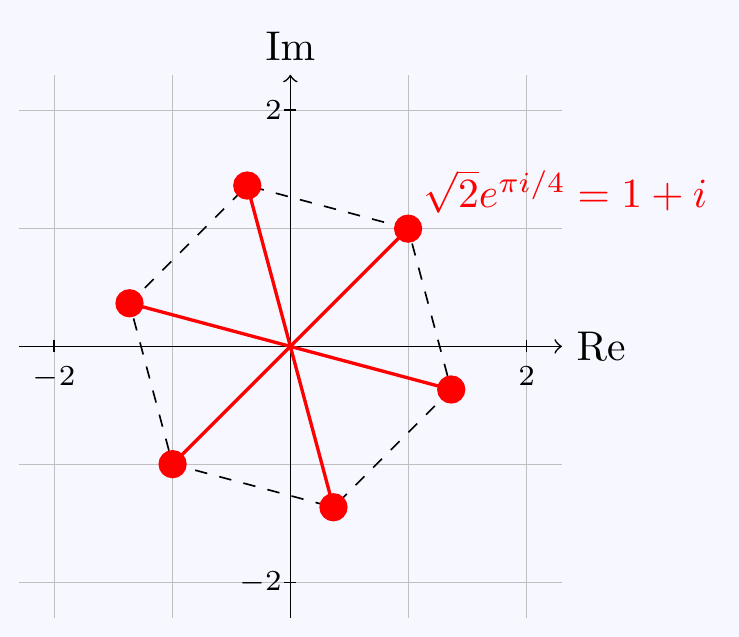
Note, we can sometimes check solutions easily. For example, the solution corresponding to $n=1$ is $z=\sqrt{2}e^{\pi i/4}=1+i$ and \[\left(\sqrt{2}e^{\pi i/4}\right)^6=2^{3}e^{3\pi i/2}=-8i\] or alternatively in Cartesian form, \[(1+i)^6=1+6i-15-20i+15+6i-1=-8i.\]

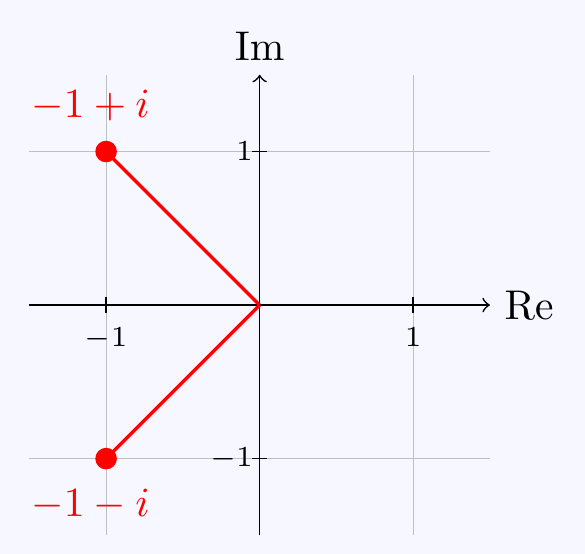
$(d)\;$ We could just use the quadratic formula. Alternatively, by completing the square: \[\begin{align*} z^2+2z+2&=(z+1)^2+1=0 \\ &\iff\quad z=-1\pm i \end{align*}\]

$(e)\;$ Tutorial question

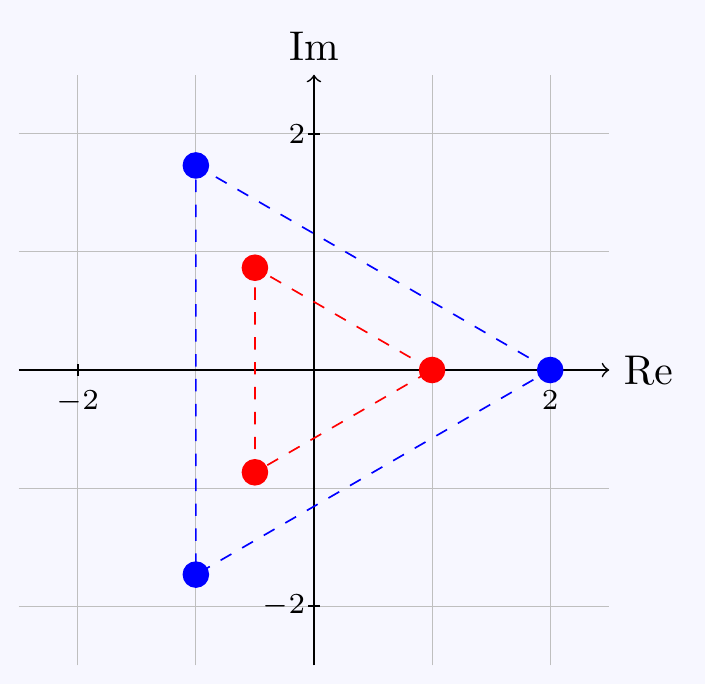
Put $w=z^3$, then $w^2-9w+8=(w-8)(w-1)=0$ so $w=z^3=1$ or $8$. Solving these two cubic equations gives roots \[z=e^{2n\pi i/3}, \;2e^{2n\pi i/3} \qquad\text{for $n=0,1,2$.}\] These six solutions can be written as $1$,$\dfrac{-1+i\sqrt3}{2}$,$\dfrac{-1-i\sqrt3}{2}$, $2$, $-1+i\sqrt3$, $-1-i\sqrt3$.

They lie at the corners of two equilateral triangles in the complex plane.

Question 2.11 $\;$ Let $P(z)=a_nz^n+a_{n-1}z^{n-1}+...+a_1z+a_0$ be a polynomial with real coefficients $a_0,a_1,...,a_n$. If $P(z)=0$, show that $P(\overline{z})=0$ as well. In other words, a polynomial with real coefficients has roots which are real or occur in pairs of complex conjugates.

Quick Check

Hint: Take complex conjugates of $P(z)$.

Solution

Consider $\overline{P(z)}=\overline{0}=0$: since $a_0,a_1,...,a_n$ are real, they are their own complex conjugates so \[\begin{align*} 0=\overline{P(z)}&=\overline{a_nz^n+a_{n-1}z^{n-1}+...+a_1z+a_0} \\ &=a_n\overline{z^n}+a_{n-1}\overline{z^{n-1}}+...+a_1\overline{z}+a_0 \\ &=a_n\overline{z}^n+a_{n-1}\overline{z}^{n-1}+...+a_1\overline{z}+a_0=P(\overline{z}). \end{align*}\]

Question 2.12 $\;$ Let $P(z)=z^4-z^3+z^2+2a$ where $a$ is a real number and suppose that $1+i$ is a root of $P(z)$.

$\;\;(a)\;$ Using the result of the previous question, find a real quadratic factor of $P(z)$.

$\;\;(b)\;$ Use $P(1+i)=0$ to find the value of $a$.

$\;\;(c)\;$ Express $P(z)$ as a product of two real quadratic factors and hence find all of its roots.

Quick Check

$(a)\;$ $(z-1-i)(z-1+i)=z^2-2z+2$ is a factor.

$(b)\;$ $a=1.$ $\hspace{1cm}$ $(c)\;$ The four roots are $1\pm i$, $\dfrac{-1\pm i\sqrt3}{2}$.

Solution

$(a)\;$ The coefficients are real so by the previous question, since $1+i$ is a root so is $1-i$. Hence \[(z-1-i)(z-1+i)=z^2-2z+2\] is a factor of $P(z)$.

$(b)\;$ As $(1+i)^2=2i$, $(1+i)^3=-2+2i$, $(1+2i)^4=-4$, \[P(1+i)=-4-(-2+2i)+2i+2a=0\quad\implies\quad a=1.\]

$(c)\;$ Comparing coefficients in \[\begin{align*} P(z)&=z^4-z^3+z^2+2=(z^2-2z+2)(bz^2+cz+d) \\ &=bz^4+(c-2b)z^3+(d-2c+2b)z^2+(2c-2d)z+2d=0 \end{align*}\] shows $b=c=d=1$, so \[ P(z)=z^4-z^3+z^2+2=(z^2-2z+2)(z^2+z+1)\] Solving the second quadratic as well shows the four roots are $1\pm i$, $\dfrac{-1\pm i\sqrt3}{2}$.

Question 2.13 $\;\;$ Find all complex solutions to the following equations

$\;\;(a)\;\; e^z=e, \hspace{1cm}$ $\;\;(b)\;\; e^z=3, \hspace{1cm}$ $\;\;(c)\;\; e^z=-3,\hspace{1cm}$ $\;\;(d)\;\; e^z=i.$

Quick Check

$(a)\;$ $z=1+2n\pi i\quad$ for $n\in\mathbb{Z}$. $\hspace{1cm}$ $(b)\;$ $z=\ln{3}+2n\pi i\quad$ for $n\in\mathbb{Z}$.

$(c)\;$ $z=\ln{3}+(2n+1)\pi i\quad$ for $n\in\mathbb{Z}$. $\hspace{1cm}$ $(d)\;$ $z=\left(\frac{\pi}{2}+2n\pi\right)i\quad$ for $n\in\mathbb{Z}$.

Solution

$(a)\;$ \[e^{x+iy}=e=e^{1+2n\pi i}\quad\implies\quad x=1,\;y=2n\pi\] and the solutions are $z=1+2n\pi i\quad$ for $n\in\mathbb{Z}$.

$(b)\;$ \[e^{x+iy}=3=3e^{2n\pi i}\quad\implies\quad x=\ln{3},\;y=2n\pi\] and the solutions are $z=\ln{3}+2n\pi i\quad$ for $n\in\mathbb{Z}$.

$(c)\;$ \[e^{x+iy}=-3=3e^{\pi i+2n\pi i}\quad\implies\quad x=\ln{3},\;y=(2n+1)\pi\] and the solutions are $z=\ln{3}+(2n+1)\pi i\quad$ for $n\in\mathbb{Z}$.

$(d)\;$ \[e^{x+iy}=i=e^0e^{\frac{\pi}{2}i+2n\pi i}\quad\implies\quad x=0,\;y=\frac{\pi}{2}+2n\pi\] and the solutions are $z=\left(\frac{\pi}{2}+2n\pi\right)i\quad$ for $n\in\mathbb{Z}$.

}

Question 2.14 $\;$ Find the principal values of the logarithms

$\;\;(a)\;\; \Ln{e},\hspace{1cm}$ $\;\;(b)\;\; \Ln{3},\hspace{1cm}$ $\;\;(c)\;\; \Ln(-3),\hspace{1cm}$ $\;\;(d)\;\; \Ln{i}.$

Quick Check

$(a)\;\; 1,\hspace{1cm}$ $(b)\;\; \ln{3},\hspace{1cm}$ $(c)\;\; \ln{3}+\pi i,\hspace{1cm}$ $(d)\;\; \frac{\pi}{2}i$.

Solution

These are the principle values of the solutions in the previous question, i.e. we use the value of $n$ that makes the imaginary part between $-\pi$ and $\pi$.

$(a)\;\;\Ln{e}=1,\hspace{1cm}$ $(b)\;\;\Ln{3}=\ln{3},\hspace{1cm}$ $(c)\;\;\Ln(-3)=\ln{3}+\pi i,\hspace{1cm}$ $(d)\;\;\Ln{i}=\frac{\pi}{2}i$.

Question 2.15 $\;$ Find all complex numbers $z$ for which

$\;\;(a)\;\; \cos{z}=2,\hspace{1cm}$ $\;\;(b)^*\;\; \sin{z}=-1,\hspace{1cm}$ $\;\;(c)\;\; \cosh{z}=-2.\hspace{1cm}$

Quick Check

$(a)\;$ $z=2n\pi-i\ln(2\pm\sqrt3).$ or $z=2n\pi\pm i\ln(2+\sqrt3)\qquad\text{for $n\in\mathbb{Z}$.}$

$(b)\;$ $z=-\frac{\pi}{2}+2n\pi\qquad\text{for $n\in\mathbb{Z}$.}$

$(c)\;$ $z=\ln(2\pm\sqrt3)+(2n+1)\pi i\qquad\text{for $n\in\mathbb{Z}$.}$

Solution

$(a)\;$ Put into exponential form and rearrange \[\begin{align*} \cos{z}=\frac{e^{iz}+e^{-iz}}{2}=2 &\quad\iff\quad e^{2iz}-4e^{iz}+1=0 \\ &\quad\iff\quad e^{iz}=\frac{4\pm\sqrt{16-4}}{2}=2\pm \sqrt{3}. \end{align*}\]

Now put $z=x+iy$ and use polar coordinates $2\pm\sqrt3=(2\pm\sqrt3)e^{2n\pi i}$ for $n\in\mathbb{Z}$: \[\begin{align*} e^{iz}=2\pm\sqrt3 &\quad\iff\qquad e^{i(x+iy)}=e^{-y}e^{ix}=(2\pm\sqrt3)e^{2n\pi i} \\ &\quad\iff\quad e^{-y}=2\pm\sqrt3\quad\text{and}\quad x=2n\pi \\ &\quad\iff\quad y=-\ln(2\pm\sqrt3)\quad\text{and}\quad x=2n\pi \\ &\quad\iff\quad z=2n\pi-i\ln(2\pm\sqrt3). \end{align*}\]

Actually, since $(2+\sqrt3)(2-\sqrt3)=1$, we have $\ln(2+\sqrt3)=-\ln(2-\sqrt3)$ so we could also
write the solutions as \[z=2n\pi\pm i\ln(2+\sqrt3)\qquad\text{for $n\in\mathbb{Z}$.}\]

$(b)\;$ Tutorial question

This time \[\begin{align*} \sin{z}=\frac{e^{iz}-e^{-iz}}{2i}=-1 &\quad\iff\quad e^{2iz}+2ie^{iz}-1=0 \\ &\quad\iff\quad e^{iz}=\frac{-2i\pm\sqrt{-4+4}}{2}=-i. \end{align*}\] Using $z=x+iy$ and $-i=e^{\left(-\frac{\pi}{2}+2n\pi\right)i}$ for $n\in\mathbb{Z}$, \[\begin{align*} e^{iz}=-i &\quad\iff\quad e^{i(x+iy)}=e^{-y}e^{ix}=e^{\left(-\frac{\pi}{2}+2n\pi\right)i} \\ &\quad\iff\quad e^{-y}=1\quad\text{and}\quad x=-\frac{\pi}{2}+2n\pi \\ &\quad\iff\quad y=0 \quad\text{and}\quad x=-\frac{\pi}{2}+2n\pi \\ &\quad\iff\quad z=-\frac{\pi}{2}+2n\pi\qquad\text{for $n\in\mathbb{Z}$.} \end{align*}\]

$(c)\;$ Now \[\begin{align*} \cosh{z}=\frac{e^z+e^{-z}}{2}=-2 &\quad\iff\quad e^{2z}+4e^{z}+1=0 \\ &\quad\iff\quad e^{z}=\frac{-4\pm\sqrt{16-4}}{2}= -2\pm\sqrt{3}. \end{align*}\] Notice that $-2\pm\sqrt3<0$ so there are no real solutions. However, we can put $z=x+iy$ and use $-2\pm\sqrt3=(2\pm\sqrt3)e^{\pi i +2n\pi i}$ for $n\in\mathbb{Z}$: \[\begin{align*} e^z=-2\pm\sqrt3 &\quad\iff\quad e^xe^{iy}=(2\pm\sqrt3)e^{\pi i+2n\pi i} \\ &\quad\iff\quad \;x=\ln(2\pm\sqrt3)\quad\text{and}\quad y=(2n+1)\pi \\ &\quad\iff\quad z=\ln(2\pm\sqrt3)+(2n+1)\pi i\qquad\text{for $n\in\mathbb{Z}$.} \end{align*}\]

Question 2.16 $\;$ For real $\theta$, use de Moivre’s theorem to express

$\;\;(a)\;\; \cos(3\theta)$ as a polynomial in $\cos\theta,\hspace{1cm}$ $\;\;(b)\;\; \sin(5\theta)$ as a polynomial in $\sin\theta$.

Quick Check

$(a)\;$ $\cos(3\theta)=4\cos^3\theta-3\cos\theta.$

$(b)\;$ $\sin(5\theta)=16\sin^5\theta-20\sin^3\theta+5\sin\theta.$

Solution

$(a)\;$ Comparing real parts in \[\begin{align*} \cos(3\theta)+i\sin(3\theta)&=\left(\cos\theta+i\sin\theta\right)^3 \\ &=\cos^3\theta+3i\cos^2\theta\sin\theta-3\cos\theta\sin^2\theta-i\sin^3\theta \end{align*}\] gives \[\begin{align*} \cos(3\theta)&=\cos^3\theta-3\cos\theta\sin^2\theta \\ &=\cos^3\theta-3\cos\theta\left(1-\cos^2\theta\right)\\ &=4\cos^3\theta-3\cos\theta. \end{align*}\]

$(b)\;$ For convenience, write $c=\cos\theta$, $s=\sin\theta$. Then by de Moivre’s theorem, we want the imaginary part of \[\begin{align*} \cos(5\theta)+i\sin(5\theta)&=(c+is)^5 \\ &=c^5+5ic^4s-10c^3s^2-10ic^2s^3+5cs^4+is^5, \end{align*}\] that is, \[\begin{align*} \sin(5\theta)&=5c^4s-10c^2s^3+s^5 \\ &=5(1-s^2)^2s-10(1-s^2)s^3+s^5 \\ &=16s^5-20s^3+5s \\ &=16\sin^5\theta-20\sin^3\theta+5\sin\theta. \end{align*}\]

Question 2.17 $\;$ Show that $\cos{4\theta}=8\cos^4\theta-8\cos^2\theta+1$ and deduce that \[\cos\frac{\pi}{8}=\frac{1}{2}\sqrt{2+\sqrt2}.\]

Quick Check

Hint: What are the four solutions of $8c^4-8c^2+1=0$? Explain why one of these values must be $\cos(\pi/8)$ and decide which one.

Solution

By de Moivre’s theorem, \[\begin{align*} \cos(4\theta)+i\sin(4\theta)&=\left(\cos\theta+i\sin\theta\right)^4 \\ &=\cos^4\theta+4i\cos^3\theta\sin\theta-6\cos^2\theta\sin^2\theta\\ &\qquad-4i\cos\theta\sin^3\theta +\sin^4\theta \end{align*}\] so comparing real parts and using $\sin^2\theta=1-\cos^2\theta$ gives \[\begin{align*} \cos(4\theta)&=\cos^4\theta-6\cos^2\theta\sin^2\theta+\sin^4\theta \\ &=\cos^4\theta-6\cos^2\theta\left(1-\cos^2\theta\right)+\left(1-\cos^2\theta\right)^2 \\ &=8\cos^4\theta-8\cos^2\theta+1. \end{align*}\] The degree 4 equation \[8c^4-8c^2+1=0\] has four solutions: in particular, solving as a quadratic in $c^2$ gives \[c^2=\frac{8\pm\sqrt{8^2-4\times 8}}{16}=\frac{2\pm\sqrt{2}}{4} \quad\implies\quad c=\pm\frac{1}{2}\sqrt{2\pm \sqrt{2}}.\] Furthermore, from the above, if $\theta$ satisfies $\cos(4\theta)=0$, then $c=\cos\theta$ is a solution. That means the four solutions must be $\cos(\pi/8)$, $\cos(3\pi/8)$, $\cos(5\pi/8)$ and $\cos(7\pi/8)$ in some order.

Finally, since $\cos(\theta)$ is decreasing for $0<\theta<\pi$, $\cos(\pi/8)$ must be the largest i.e. take the positive signs.

Question 2.18 $\;$ For real $\theta$, use de Moivre’s theorem to show that

$\;\;(a)\;\; \cos^3\theta=\dfrac{\cos(3\theta)+3\cos\theta}{4}, \hspace{1cm}$ $\;\;(b)^*\;\; \cos^4\theta=\dfrac{\cos(4\theta)+4\cos(2\theta)+3}{8}.$

Quick Check

$(a)\;$ Express $\cos(3\theta)$ in terms of $\cos\theta$ and rearrange. Alternatively, expand $\cos^3\theta=\left(\dfrac{e^{i\theta}+e^{-i\theta}}{2}\right)^3$ and recombine.

$(b)\;$ similar but with $\sin$.

Solution

$(a)\;$ This follows by using Question $5.8(a)$. Alternatively, using $\cos\theta=\dfrac{z+z^{-1}}{2}$ where $z=e^{i\theta}$, \[\begin{align*} \cos^3\theta=\left(\frac{z+z^{-1}}{2}\right)^3 &=\frac18\left(z^3+3z+3z^{-1}+z^{-3}\right) \\ &=\frac14\left(\frac{z^3+z^{-3}}{2}\right) +\frac34\left(\frac{z+z^{-1}}{2}\right) \\ &=\frac{\cos(3\theta)+3\cos\theta}{4}. \end{align*}\]

$(b)\;$ Tutorial question

Similarly, \[\begin{align*} \cos^4\theta=\left(\frac{z+z^{-1}}{2}\right)^4 &=\frac{1}{16}\left(z^4+4z^2+6+4z^{-2}+z^{-4}\right) \\ &=\frac18\left(\frac{z^4+z^{-4}}{2}\right) +\frac12\left(\frac{z+z^{-1}}{2}\right)+\frac38 \\ &=\frac{\cos(4\theta)+4\cos(2\theta)+3}{8}. \end{align*}\]

Question 2.19 $\;$ For real $\theta$, use de Moivre’s theorem to express

$\;\;(a)\;\; \sin^3\theta$ as a combination of $\sin(3\theta)$ and $\sin\theta$,

$\;\;(b)\;\; \sin^4\theta$ as a combination of $\cos(4\theta)$ and $\cos(2\theta)$.

Quick Check

$(a)\;$ $\sin^3(\theta)=\dfrac{3\sin\theta-\sin(3\theta)}{4}$, $\hspace{1cm}$ $(b)\;$ $\sin^4(\theta)=\dfrac{\cos(4\theta)-4\cos(2\theta)+3}{8}$.

Solution

$(a)\;$ Using $\sin\theta=\dfrac{z-z^{-1}}{2i}$ where $z=e^{i\theta}$, \[\begin{align*} \sin^3\theta=\left(\frac{z-z^{-1}}{2i}\right)^3 &=\frac{1}{-8i}\left(z^3-3z+3z^{-1}-z^{-3}\right) \\ &=\frac34\left(\frac{z-z^{-1}}{2i}\right) -\frac14\left(\frac{z^3-z^{-3}}{2i}\right)\\ &=\frac{3\sin\theta-\sin(3\theta)}{4}. \end{align*}\]

$(b)\;$ Similarly, \[\begin{align*} \sin^4\theta=\left(\frac{z-z^{-1}}{2i}\right)^4 &=\frac{1}{16}\left(z^4-4z^2+6-4z^{-2}+z^{-4}\right) \\ &=\frac18\left(\frac{z^4+z^{-4}}{2}\right) -\frac12\left(\frac{z+z^{-1}}{2}\right)+\frac38 \\ &=\frac{\cos(4\theta)-4\cos(2\theta)+3}{8}. \end{align*}\]

Alternatively, one can expand $\cos(4\theta)+i\sin(4\theta)=(\cos\theta+i\sin\theta)^4$, etc. and use $\cos^2\theta+\sin^2\theta=1$ to simplify.

Question 2.20 $\;$ Given that \[1+z+z^2+z^3+...=\sum_{n=0}^{\infty}z^n=\frac{1}{1-z}\quad\text{for $|z|<1$}\] use de Moivre’s theorem to calculate the following infinite sums for real $\theta$:

$\;\;(a)\;\; \displaystyle\sum_{n=0}^{\infty}\left(\frac{1}{2}\right)^n\cos(n\theta),\hspace{1cm}$ $\;\;(b)\;\; \displaystyle\sum_{n=0}^{\infty}\left(\frac{1}{2}\right)^n\sin(n\theta).$

Quick Check

Hint: do both at once by using $e^{in\theta}=\cos(n\theta)+i\sin(n\theta)$.

Then apply the geometric sum with $z=\dfrac12e^{i\theta}$ and rewrite in terms of $\cos$ and $\sin$. You should find

$(a)\;$ $\dfrac{4-2\cos\theta}{5-4\cos\theta}$, $\hspace{1cm}$ $(b)\;$ $\dfrac{2\sin\theta}{5-4\cos\theta}$.

Solution

Parts $(a)$ and $(b)$ are the real and imaginary parts of \[\sum_{n=0}^{\infty}\left(\frac12\right)^ne^{in\theta} =\sum_{n=0}^{\infty}\left(\frac12e^{i\theta}\right)^n =\frac{1}{1-\frac12e^{i\theta}}=\frac{2}{2-e^{i\theta}}\] (This is valid since $|\frac12e^{i\theta}|=\frac12<1$.) Also, multiplying top and bottom by the conjugate: \[\begin{align*} \frac{2}{2-e^{i\theta}}=\frac{2(2-e^{-i\theta})}{(2-e^{i\theta})(2-e^{-i\theta})} &=\frac{4-2e^{-i\theta}}{4-2e^{i\theta}-2e^{-i\theta}+1} \\ &=\frac{4-2(\cos\theta-i\sin\theta)}{5-4\cos\theta}. \end{align*}\] Hence by taking real and imaginary parts we find

$(a)\;$ $\displaystyle\sum_{n=0}^{\infty}\left(\frac{1}{2}\right)^n\cos(n\theta)= \frac{4-2\cos\theta}{5-4\cos\theta}$,

$(b)\;$ $\displaystyle\sum_{n=0}^{\infty}\left(\frac{1}{2}\right)^n\sin(n\theta)= \frac{2\sin\theta}{5-4\cos\theta}$.

Question 2.21 $\;$ Use the definitions \[\cos{z}=\dfrac{e^{iz}+e^{-iz}}{2} \quad\text{and}\quad \sin{z}=\dfrac{e^{iz}-e^{-iz}}{2i}\] to show that

$\;\;(a)\;\; \sin(z+w)=\sin{z}\cos{w}+\cos{z}\sin{w},$

$\;\;(b)\;\; \cos(z+w)=\cos{z}\cos{w}-\sin{z}\sin{w}.$

In other words, prove the usual double angle formulae hold for all complex $z$ and $w$.

Quick Check

Hint: start from the (more complicated) right-hand sides and simplify.

Solution

$(a)\;$ Start from the (more complicated) right-hand side and simplify \[\begin{align*} \sin{z}\cos{w}+\cos{z}\sin{w}&= \left(\dfrac{e^{iz}-e^{-iz}}{2i}\right)\left(\dfrac{e^{iw}+e^{-iw}}{2}\right) \\ &\qquad\qquad\qquad +\left(\dfrac{e^{iz}+e^{-iz}}{2}\right)\left(\dfrac{e^{iw}-e^{-iw}}{2i}\right) \\ &=\frac{e^{i(z+w)}+e^{i(z-w)}-e^{-i(z-w)}-e^{-i(z+w)}}{4} \\ &\qquad\qquad\qquad +\frac{e^{i(z+w)}-e^{i(z-w)}+e^{-i(z-w)}-e^{-i(z+w)}}{4i} \\ &=\dfrac{e^{i(z+w)}-e^{-i(z+w)}}{2i} \\ &=\sin(z+w). \end{align*}\]

Similarly, \[\begin{align*} \cos{z}\cos{w}-\sin{z}\sin{w}&= \left(\dfrac{e^{iz}+e^{-iz}}{2}\right)\left(\dfrac{e^{iw}+e^{-iw}}{2}\right) \\ &\qquad\qquad\qquad -\left(\dfrac{e^{iz}-e^{-iz}}{2i}\right)\left(\dfrac{e^{iw}-e^{-iw}}{2i}\right) \\ &=\frac{e^{i(z+w)}+e^{i(z-w)}+e^{-i(z-w)}+e^{-i(z+w)}}{4} \\ &\qquad\qquad\qquad+\frac{e^{i(z+w)}-e^{i(z-w)}-e^{-i(z-w)}+e^{-i(z+w)}}{4} \\ &=\dfrac{e^{i(z+w)}+e^{-i(z+w)}}{2} \\ &=\cos(z+w). \end{align*}\]

Question 2.22 $\;$ Recall the hyperbolic functions: \[\cosh{y}=\dfrac{e^y+e^{-y}}{2} \quad\text{and}\quad \sinh{y}=\dfrac{e^y-e^{-y}}{2}.\] Show that for an arbitrary complex number $z=x+iy$,

$\;\;(a)\;\; \sin{z}=\sin{x}\cosh{y}+i\cos{x}\sinh{y},\hspace{1cm}$

$\;\;(b)\;\; |\sin{z}|=\sqrt{\sin^2{x}+\sinh^2{y}}$.

Find similar formulae for $\cos{z}$ and $|\cos{z}|$.

Quick Check

Hint: start from the (more complicated) right-hand sides and simplify.

Solution

$(a)\;$ One way to do this is to write out the right-hand side in terms of exponentials and then multiply out the brackets, just as in the last question. Alternatively, using the result from the last question, \[\sin(x+iy)=\sin{x}\cos(iy)+\cos{x}\sin(iy)\] and then substitute \[\cos(iy)=\frac{e^{i(iy)}+e^{-i(iy)}}{2}=\frac{e^{-y}+e^{y}}{2}=\cosh{y}\] and \[\sin(iy)=\frac{e^{i(iy)}-e^{-i(iy)}}{2i}=\frac{e^{-y}-e^{y}}{2i} =\frac{-\sinh{y}}{i}=i\sinh{y}.\]

$(b)\;$ Using part $(a)$ we get \[\begin{align*} |\sin(x+iy)|^2&=\sin^2{x}\cosh^2{y}+\cos^2{x}\sinh^2{y} \\ &=\sin^2{x}(1+\sinh^2{y})+(1-\sin^2{x})\sinh^2{y} \\ &=\sin^2{x}+\sinh^2{y} \end{align*}\] and taking square roots (which is okay since all terms are non-negative) gives the result.

Week 6 Material

Question 2.23 $\;$ Suppose the points $A$, $B$, $C$ and $D$ represent the complex numbers $z_1$, $z_2$, $z_3$ and $z_4$ respectively, and $O$ is the origin $z=0$.

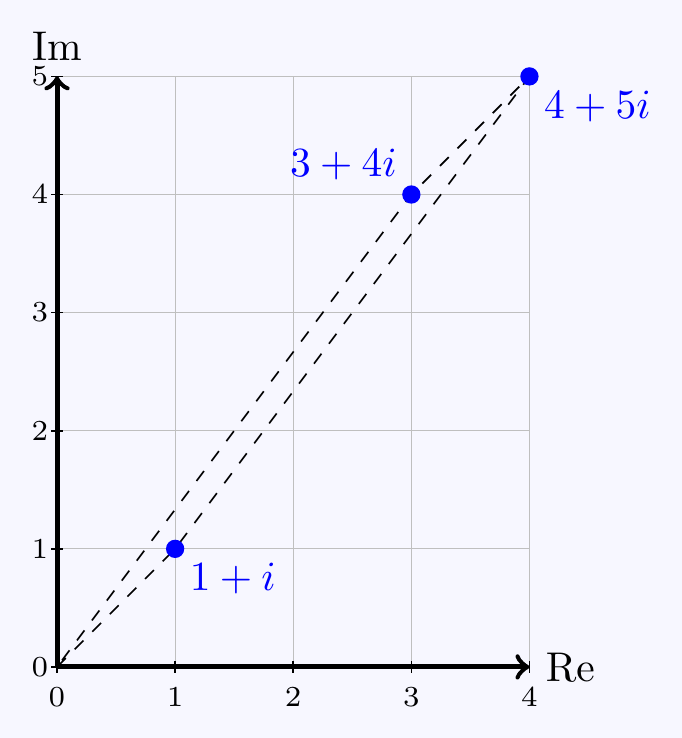
$\;\;(a)\;\;$ If $OABC$ is a parallelogram and $z_1=1+i$ and $z_2=4+5i$, find $z_3$.

$\;\;(b)\;\;$ If $ABCD$ is a square, find $z_2$ and $z_4$ in the cases

$\hspace{1.5cm}(i)\;\; z_1=2+i$ and $z_3=6+7i\hspace{1cm}$ $(ii)\;\; z_1=6-2i$ and $z_3=6i$.

Quick Check

$(a)\;$ $z_3=3+4i.$

$(b)\;(i)\;$ $z_2=7+2i, \; z_4= 1+6i$ and $\;\;\;\;(ii)\;$ $z_2=7+5i, \; z_4=-1-i$.

Solution

$(a)\;$ The points $0$, $z_1$, $z_2$ and $z_3$ form a (very thin) parallelogram when $z_2=z_1+z_3$ so \[z_3=(4+5i)-(1+i)=3+4i.\]

$(b)\;(i)\;$ The centre of the square is the midpoint between $z_1$ and $z_3$, i.e \[z_0=\frac{z_1+z_3}{2}=4+4i.\]

We can find the line connecting $z_2$ and $z_0$ by rotating the line connecting $z_1$ to $z_0$ through an angle $\pi/2$, i.e. by multiplying by $e^{\pi i/2}=i$ \[\begin{align*} z_2-z_0&=(z_1-z_0)i \\ \implies\qquad z_2&=z_0+(z_1-z_0)i \\ &=4+4i+(2+i-4-4i)i=7+2i \end{align*}\] Similarly, \[\begin{align*} z_4&=z_0+(z_3-z_0)i \\ &=4+4i+(6+7i-4-4i)i=1+6i \end{align*}\]

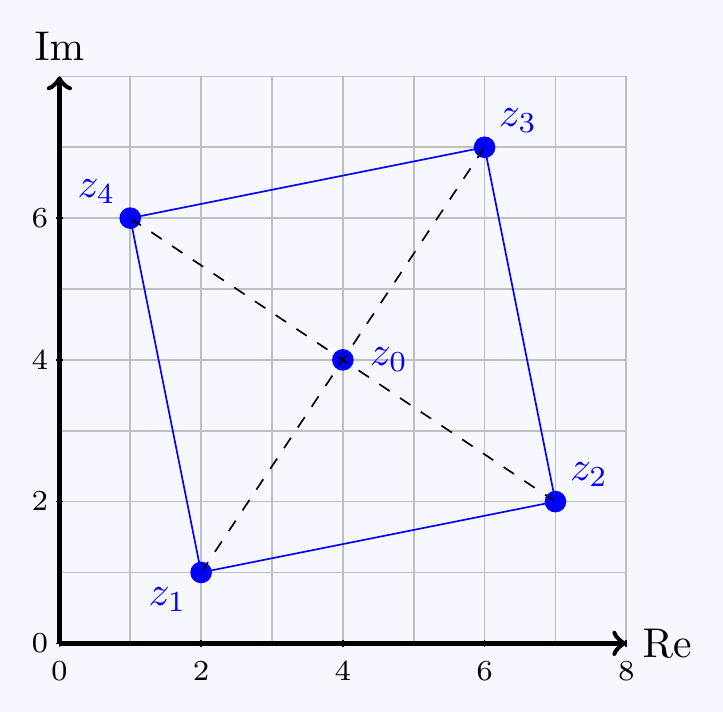
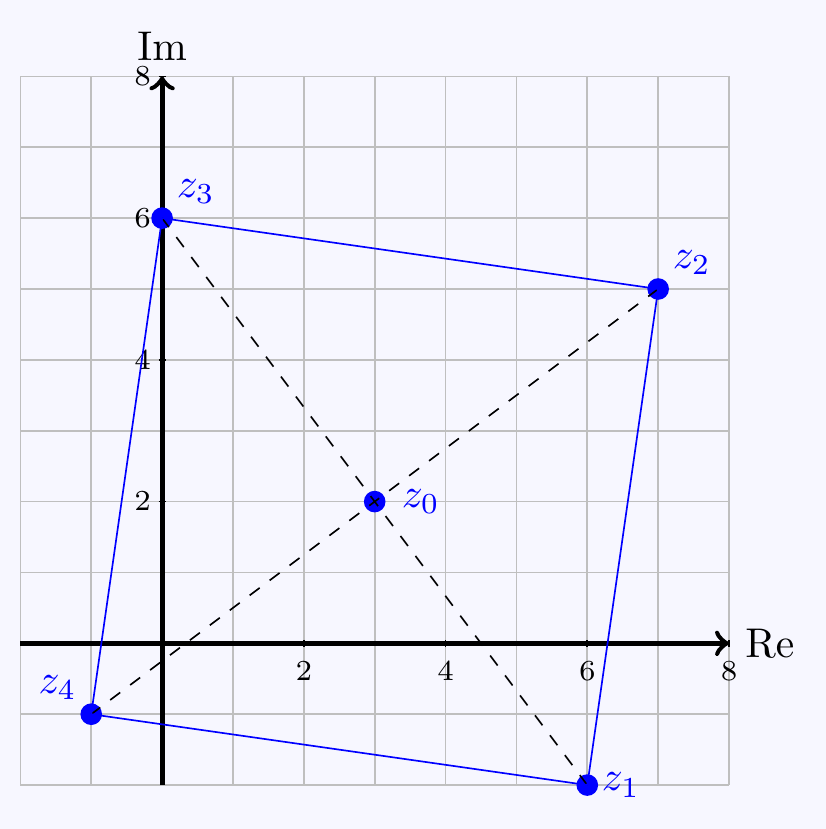
$(b)\;(ii)\;$ Following the same procedure, we generally get
\[z_2,z_4 = \frac{z_1+z_3}{2}\pm\left(\frac{z_1-z_3}{2}\right)i\] which in this case gives $z_2=7+5i$ and $z_4=-1-i$.

Question 2.24 $\;$ Three points $z_1$, $z_2$ and $z_3$ form an equilateral triangle in the complex plane. Given that $z_1=2+i$ and $z_2=3+i(1+\sqrt{3})$,

$\;\;(a)\;\;$ Find the modulus and argument of $z_2-z_1$.

$\;\;(b)\;\;$ Find the modulus of $z_3-z_1$.

$\;\;(c)\;\;$ Find the possible arguments of $z_3-z_1$.

$\;\;(d)\;\;$ Hence find the possible values of $z_3$.

Quick Check

$(a)\;$ $|z_2-z_1|=2 \quad\text{and}\quad \operatorname{Arg}(z_2-z_1)=\frac{\pi}{3}.$

$(b)\;$ $|z_3-z_1|=2$.

$(c)\;$ $\arg(z_3-z_1)=0 \quad\text{or}\quad 2\pi/3$.

$(d)\;$ $z_3=4+i\quad\text{or}\quad 1+i(1+\sqrt3)$.

Solution

Notice there will be two choices for $z_3$ and two possible triangles.

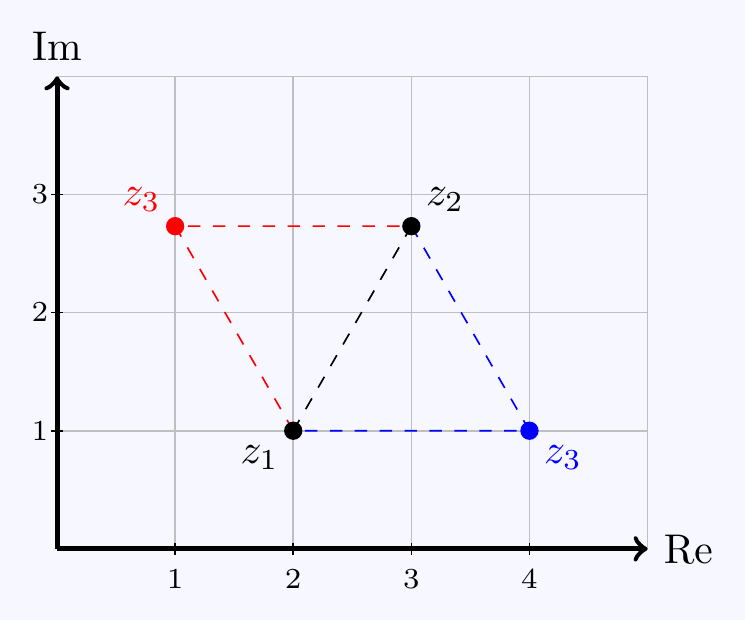
$(a)\;$ As $z_2-z_1=1+i\sqrt3$, we have $|z_2-z_1|=\sqrt{1+3}=2$ and \[\Arg(z_2-z_1)=\arctan\left(\dfrac{\sqrt3}{1}\right)=\dfrac{\pi}{3}.\]

$(b)\;$ The side lengths of the triangle are equal so $|z_3-z_1|=|z_2-z_1|=2$.

$(c)\;$ The internal angles in an equilateral triangle are $\pi/3$. We know the edge connecting
$z_1$ to $z_2$ makes angle $\pi/3$ with the real axis. That means the edge connecting $z_1$ to $z_3$ must make angle $\arg(z_3-z_1)=\pi/3\pm\pi/3=0$ or $2\pi/3$.

$(d)\;$ Knowing the modulus and argument means we know $z_3-z_1$ exactly: \[z_3-z_1=2 \quad\text{or}\quad z_3-z_1=2e^{2\pi i/3}=-1+i\sqrt3.\] Hence $z_3=4+i\quad\text{or}\quad 1+i(1+\sqrt3)$.

Question 2.25 $\;$ A regular hexagon in the complex plane has centre $z_0=3+i$ and one of the vertices at $z_1=3+3i$. Find the other vertices of the hexagon.

Quick Check

The six vertices are $3 + 3i,\; 3-i, \; 3\pm\sqrt3,\; 3\pm\sqrt3+2i$.

Solution

Call the other vertices $z_2,...,z_6$. Then the line connecting $z_{n+1}$ to $z_0$ is obtained by rotating the line connecting $z_1$ to $z_0$ through angle $n\pi/3$.

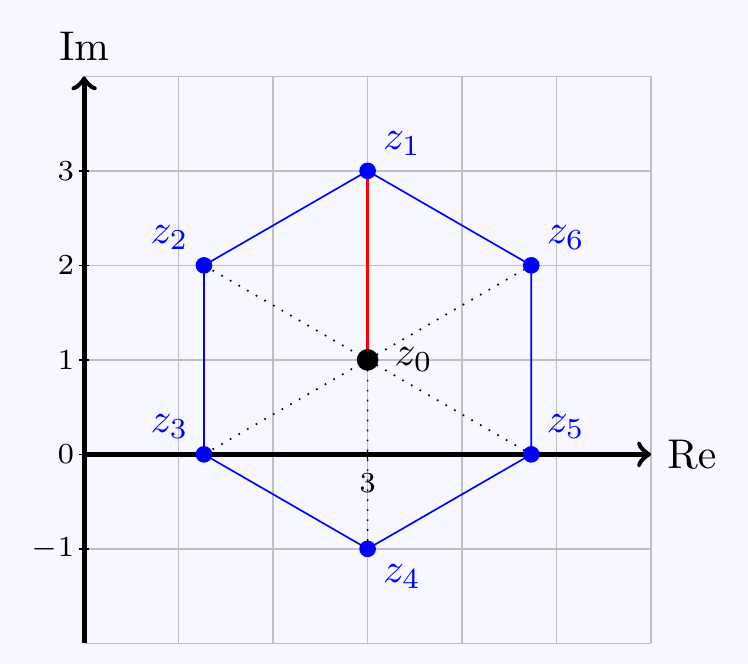
We can find the vertices by multiplying by $e^{n\pi i/3}$. \[\begin{align*} z_{n+1}-z_0=e^{n\pi i/3}(z_1-z_0) =2ie^{n\pi i/3} \end{align*}\] so \[z_{n+1}=3+i+2ie^{n\pi i/3}.\] Substituting in $n=0,...,5$ give the six vertices $3 + 3i,\; 3-i, \; 3\pm\sqrt3,\; 3\pm\sqrt3+2i$.

Question 2.26 $\;$ Sketch the set of numbers $z$ in the complex plane satisfying:

$\;\;(a)\;\;|z|=2,\hspace{3.4cm}$ $\;\;(b)\;\;|z-2|=|z+2|,\hspace{1.5cm}$ $\;\;(c)^*\;\;\sqrt{3}\;|z-2|=|z+2|,$

$\;\;(d)\;\;|z-2|+|z+2|=6,\hspace{1cm}$ $\;\;(e)^*\;\;\arg\left(\dfrac{z-2}{z+2}\right)=\dfrac{\pi}{2},\hspace{1cm}$ $\;\;(f)\;\;\arg\left(\dfrac{z-2}{z+2}\right)=\dfrac{\pi}{4}$.

Quick Check

Hint: Either work geometrically in terms of lengths and angles, or set $z=x+iy$ and rewrite the conditions in terms of $x$ and $y$.

Solution

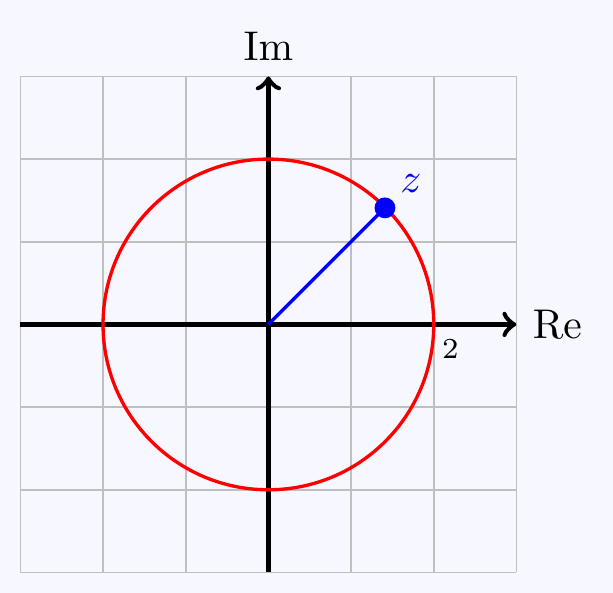
$(a)\;$ We have $|x+iy|=2\quad\iff\quad x^2+y^2=4$.

Alternatively, notice $|z|=2$ is the set of points distance $2$ from the origin, i.e. it’s a circle.

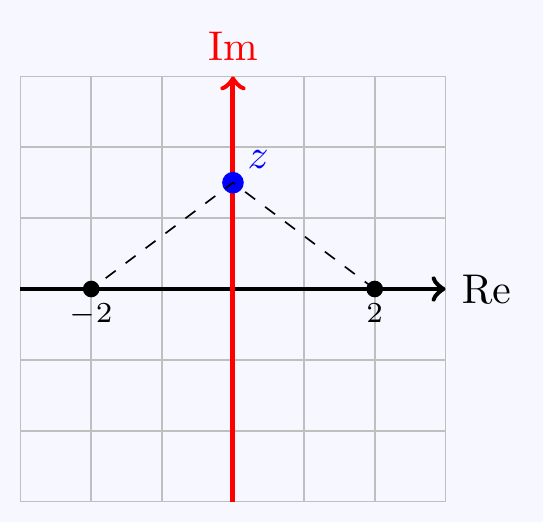
$(b)\;$ We have $(x-2)^2+y^2=(x+2)^2+y^2\quad\iff\quad x=0$.

We can alternatively see that $|z-2|=|z+2|$ is the set of points equal distance from the point $2$ and $-2$. This is the imaginary axis.

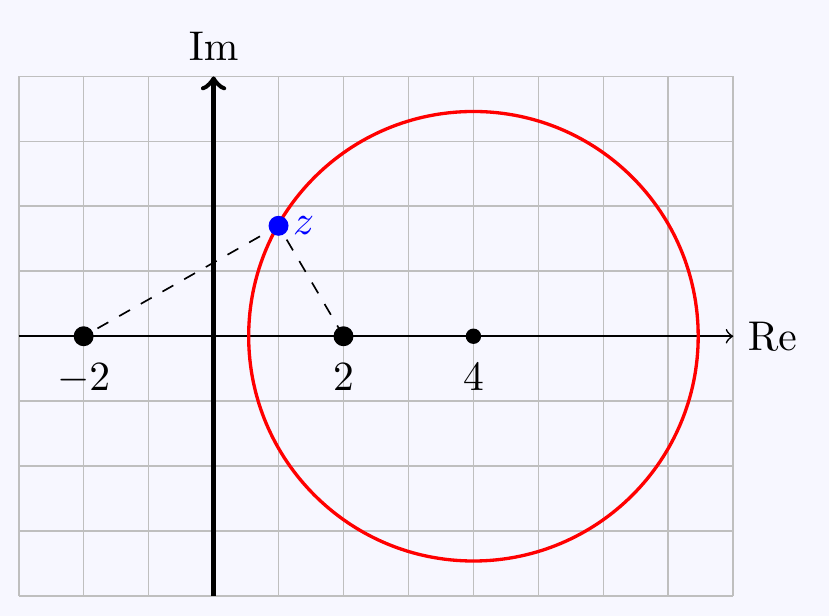
$(c)\;$ Tutorial question

Putting $z=x+iy$ and squaring gives \[\begin{align*} 3|x+iy-2|^2&=|x+iy+2|^2 \\ \qquad\iff\; 3\left((x-2)^2+y^2\right)&=(x-2)^2+y^2 \\ \qquad\iff\;\, x^2-8x+4+y^2&=0 \\ \qquad\iff\qquad (x-4)^2+y^2&=12 \end{align*}\] which is a circle with centre at $z=4$ and radius $\sqrt{12}$.

Generalising parts $(b)$ and $(c)$, one can show that the set of points $z$ with constant ratio of distances $|z-z_1|/|z-z_2|=c$ is a straight line if $c=1$ and a circle otherwise.

$(d)\;$ We can do this algebraically (though it’s a bit tedious). Put $z=x+iy$, then \[|x-2+iy|+|x+2+iy|=6 \qquad\iff\qquad \sqrt{(x-2)^2+y^2}+\sqrt{(x+2)^2+y^2}=6 \] \[\begin{align*} &\qquad\iff\qquad \sqrt{(x-2)^2+y^2}=6-\sqrt{(x+2)^2+y^2} \\ &\qquad\iff\qquad (x-2)^2+y^2=36+(x+2)^2+y^2-12\sqrt{(x+2)^2+y^2} \\ &\qquad\iff\qquad 12\sqrt{(x+2)^2+y^2}=36+(x+2)^2-(x-2)^2=36+8x \\ &\qquad\iff\qquad 3\sqrt{(x+2)^2+y^2}=9+2x \\ &\qquad\iff\qquad 9(x+2)^2+9y^2=81+36x+4x^2 \\ &\qquad\iff\qquad 5x^2+9y^2=45 \\ &\qquad\iff\qquad \bigg(\,\frac{x}{3}\,\bigg)^2+\bigg(\frac{y}{\sqrt5}\bigg)^2=1. \end{align*}\] This is the equation of an ellipse.

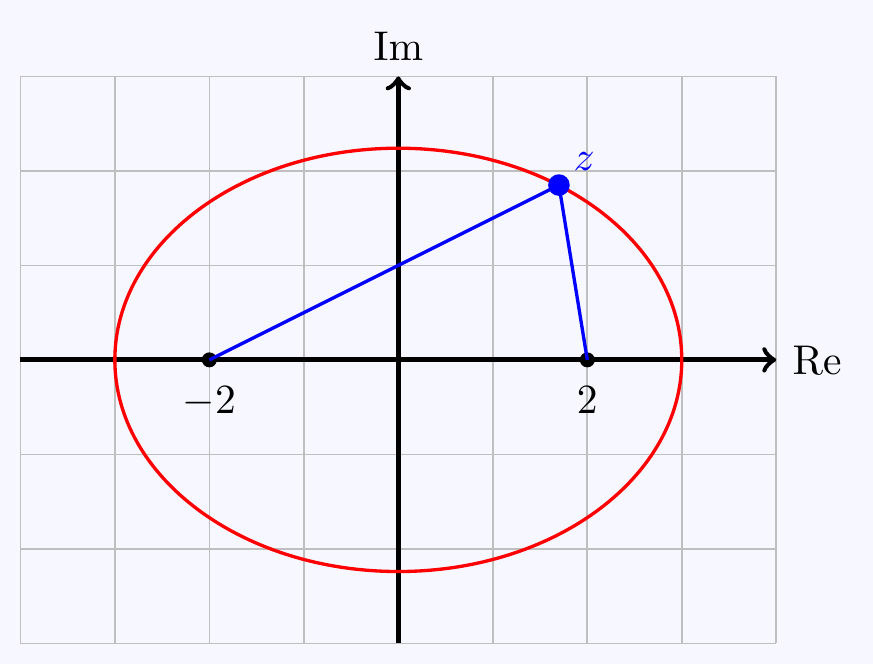
A nice geometric way to see this is if we know the defining property of an ellipse - it’s the set of points with constant sum of distances from two points. That’s exactly what the equation $|z-2|+|z+2|=6$ says.

$(e)\;$ Tutorial question

Putting $z=x+iy$, \[\begin{align*} \frac{z-2}{z+2}=\frac{x-2+iy}{x+2+iy}&=\frac{(x-2+iy)(x+2-iy)}{(x+2)^2+y^2}\\ &=\frac{x^2+y^2-4}{(x+2)^2+y^2}+i\frac{4y}{(x+2)^2+y^2} \end{align*}\] so \[\tan\arg\left(\frac{z-2}{z+2}\right)=\frac{4y}{x^2+y^2-4} =\tan\left(\frac{\pi}{2}\right)=\infty.\] We must have $x^2+y^2-4=0$, i.e. $z=x+iy$ lies on the circle $x^2+y^2=4$.

Geometrically, we could see this by looking at the angles in the right-angled triangle shown here.

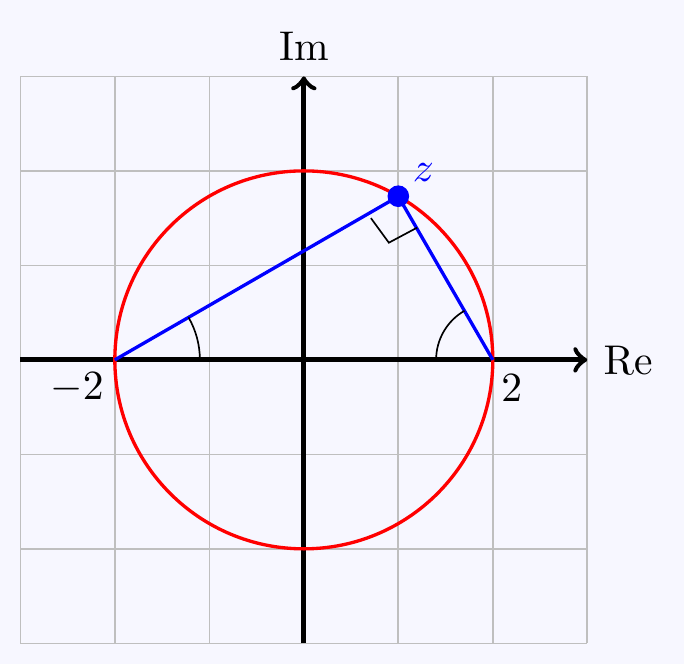
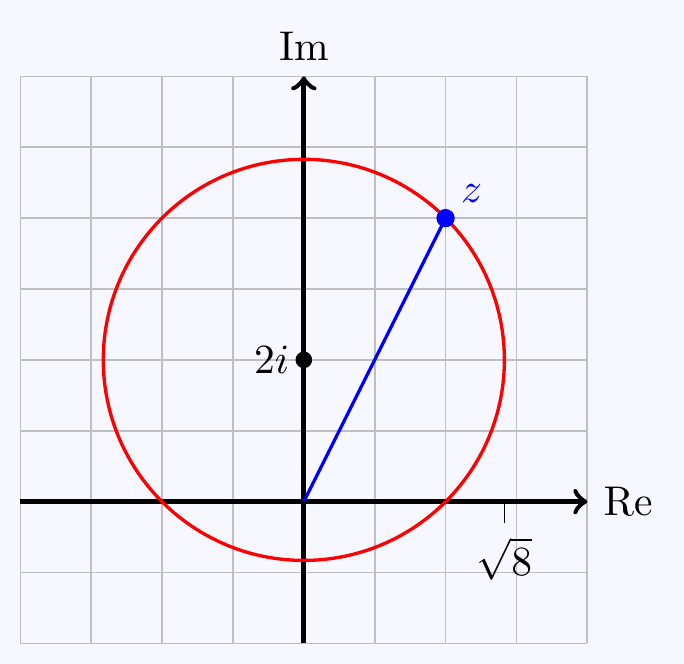
$(f)\;$ We have \[\tan\arg\left(\frac{z-2}{z+2}\right)=\frac{4y}{x^2+y^2-4} =\tan\left(\frac{\pi}{4}\right)=1\] \[\implies\qquad x^2+y^2-4y-4=0\qquad\implies\qquad x^2+(y-2)^2=8\] So $z=x+iy$ lies on a circle centre $2i$ and radius $\sqrt8$.

Question 2.27 $\;$ Find the unique complex number $z$ satisfying \[|z-1-3i|=|z-1-i|\qquad\text{and}\qquad\Arg(z)=\frac{\pi}{4}.\] (You can do this algebraically, but there is a quick geometric way too.)

Quick Check

You should find $z=2+2i$.

Solution

Let $z=x+iy$. Then \[\begin{align*} |z-1-3i|^2=|z-1-i|^2 &\qquad\implies\qquad (x-1)^2+(y-3)^2=(x-1)^2+(y-1)^2 \\ &\qquad\implies\qquad (y-3)^2=(y-1)^2 \\ &\qquad\implies\qquad y^2-6y+9=y^2-2y+1 \quad\implies\quad y=2 \end{align*}\] Also, $\Arg(z)=\pi/4$ implies $\arctan(y/x)=\pi/4$ and so $x=y=2$. We have $z=2+2i$.

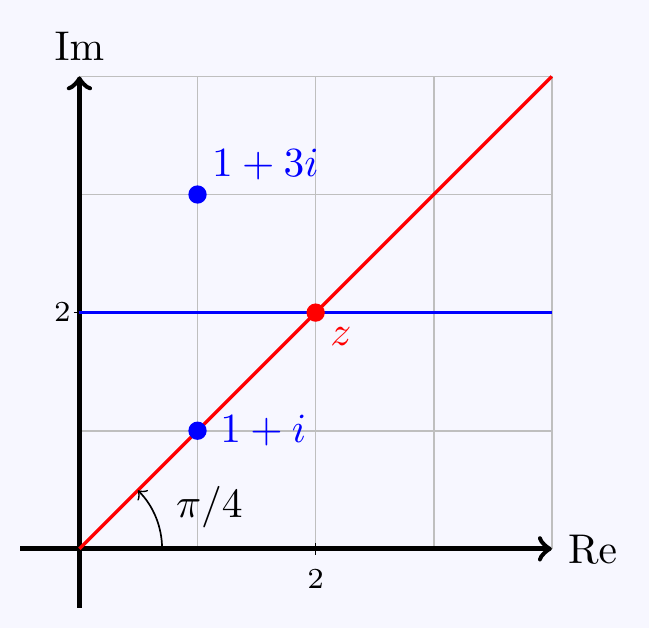
Geometrically, $\Arg(z)=\pi/4$ means $z$ makes an angle $\pi/4$ with the real axis, so $x=y$.

Also, $|z-1-3i|=|z-1-i|$ means $z$ is on the line bisecting $1+3i$ and $1+i$, so $y=2$.

Thus $z$ is just the intersection of these two lines.

Question 2.28 $\;$ Describe the sets of complex numbers such that

$\;\;(a)\;\;$ $w=(z-i)/(z-1)$ is a real number,

$\;\;(b)\;\;$ $w=(z-i)/(z-1)$ is purely imaginary.

$\;\;$(Hint: $w$ is real exactly when $w=\overline{w}$ and is purely imaginary when $w=-\overline{w}$.

$\;\;$ Use this to find a relationship between $x=\Re(z)=\dfrac{z+\overline{z}}{2}$ and $y=\Im(z)=\dfrac{z-\overline{z}}{2i}$.)

Quick Check

This is quite difficult, but can be done using the hint and some careful algebra.

Solution

Caution: this one is quite tricky. There are multiple ways to do it, but it can easily turn into a horrible mess of algebra. For both parts, we will use the fact that conjugation respects sums, products and quotients, and so \[\overline{w}=\frac{\overline{z}+i}{\overline{z}-1}.\] We will also use the formulas that express real and imaginary parts using $z$ and $\overline{z}$: \[x=\Re(z)=\frac{z+\overline{z}}{2} \quad\text{and}\quad y=\Im(z)=\frac{z-\overline{z}}{2i}.\]

$(a)\;$ We have $w$ is real precisely when \[\begin{align*} w=\overline{w} &\quad\iff\quad \frac{z-i}{z-1}=\frac{\overline{z}+i}{\overline{z}-1} \\ &\quad\iff\quad (z-i)(\overline{z}-1)=(z-1)(\overline{z}+i) \\ &\quad\iff\quad z\overline{z}-i\overline{z}-z+i=z\overline{z}-\overline{z}+iz-i \\ &\quad\iff\quad i(z+\overline{z})+(z-\overline{z})=2i \\ &\quad\iff\quad \left(\frac{z+\overline{z}}{2}\right)+\left(\frac{z-\overline{z}}{2i}\right)=1 \\ &\quad\iff\quad x+y=1. \end{align*}\] This means that $z$ lies on the line $y=1-x$. However, we can’t have $z=1$ since the fraction $w$ then doesn’t make sense. Thus the set of points is this line with the point $z=1$ removed.

$(b)\;$ This time $w$ is purely imaginary when \[\begin{align*} w=-\overline{w} &\quad\iff\quad \frac{z-i}{z-1}=-\frac{\overline{z}+i}{\overline{z}-1} \\ &\quad\iff\quad (z-i)(\overline{z}-1)=-(z-1)(\overline{z}+i) \\ &\quad\iff\quad z\overline{z}-i\overline{z}-z+i=-z\overline{z}+\overline{z}-iz+i \\ &\quad\iff\quad 2z\overline{z}-(z+\overline{z})+i(z-\overline{z})=0 \\ &\quad\iff\quad z\overline{z}-\left(\frac{z+\overline{z}}{2}\right)-\left(\frac{z-\overline{z}}{2i}\right)=0 \\ &\quad\iff\quad x^2+y^2-x-y=0 \\ &\quad\iff\quad \left(x-\frac12\right)^2+\left(y-\frac12\right)^2=\frac12 \end{align*}\] where in the last step we have completed the squares. This is the equation of a circle in the complex plane with centre at $\dfrac{1+i}{2}$ and radius $\dfrac{\sqrt2}{2}$. However, again we can’t have $z=1$ and so the set of points is this circle with the point $z=1$ removed.

Question 2.29 $\;$ In a series RLC circuit, the complex impedance $Z$ depends on the (real-valued) frequency $\omega$ via the formula \[Z(\omega)=R+i\omega L+\frac{1}{i\omega C}\] where the capacitance $C$, inductance $L$ and resistance $R$ are real constants.

$\;\;(a)\;\;$ Find, in terms of $L$ and $C$, the resonant frequency of the circuit,

$\qquad\;\,$ i.e. the frequency $\omega_0$ at which the impedance $Z(\omega_0)$ has minimal modulus.

$\;\;(b)\;\;$ Show that \[\frac{Z(\omega)}{Z(\omega_0)}= 1+iQ\left(\frac{\omega}{\omega_0}-\frac{\omega_0}{\omega}\right)\] $\qquad\;\,$ for some real constant $Q$ (this is called the ``$Q$ factor” of the circuit).

$\;\;(c)\;\;$ Find, in terms of $\omega_0$ and $Q$, the values of $\omega$ for which the ratio in part $(b)$ has modulus $\sqrt{2}$.

$\;\;(d)\;\;$ Given that the complex voltage $\widehat{V}$ and current $\widehat{I}$ are related by $\widehat{V}=\widehat{I}Z(\omega)$, find the

$\qquad\;\,$ phase difference $\Arg(\widehat{V})-\Arg(\widehat{I})$ in terms of $Q$, $\omega$ and $\omega_0$.

Quick Check

$(a)\;$ $\omega_0=\dfrac{1}{\sqrt{LC}}$.

$(b)\;$ You should find $Q=\dfrac{1}{R}\sqrt{\dfrac{L}{C}}$

$(c)\;$ $\omega=\dfrac{\omega_0}{2Q}\left(\pm 1\pm\sqrt{1+4Q^2}\right).$

$(d)\;$ $\operatorname{Arg}(V)-\operatorname{Arg}(I)=\arctan\left(Q\left(\dfrac{\omega}{\omega_0}-\dfrac{\omega_0}{\omega}\right)\right).$

Solution

$(a)\;$ We have $Z(\omega)=R+i\left(\omega L-\dfrac{1}{\omega C}\right)$ and so \[ |Z(\omega)|^2=R^2+\left(\omega L-\dfrac{1}{\omega C}\right)^2.\] This will be minimal when $\omega L-\dfrac{1}{\omega C}=0$, i.e. when $\omega^2=\dfrac{1}{LC}$ and so $\omega_0=\dfrac{1}{\sqrt{LC}}$.

$(b)\;$ Since $Z(\omega_0)=R$, we have \[\begin{align*} \frac{Z(\omega)}{Z(\omega_0)} &=1+i\left(\frac{\omega L}{R}-\frac{1}{RC\omega}\right) \\ &=1+i\left(\frac{\omega_0 L}{R}\frac{\omega}{\omega_0}- \frac{1}{\omega_0 RC}\frac{\omega_0}{\omega}\right) \\ &=1+i\left(\frac{1}{R}\sqrt{\frac{L}{C}}\frac{\omega}{\omega_0}- \frac{1}{R}\sqrt{\frac{L}{C}}\frac{\omega_0}{\omega}\right) \\ &=1+iQ\left(\frac{\omega}{\omega_0}-\frac{\omega_0}{\omega}\right) \end{align*}\] where $Q=\dfrac{1}{R}\sqrt{\dfrac{L}{C}}$.

$(c)\;$ The modulus squared is $2$, that is, \[\begin{align*} \left|\frac{Z(\omega)}{Z(\omega_0)}\right|^2 &=1+Q^2\left(\frac{\omega}{\omega_0}-\frac{\omega_0}{\omega}\right)^2=2 \\ &\implies\quad Q\left(\frac{\omega}{\omega_0}-\frac{\omega_0}{\omega}\right)=\pm 1 \\[5pt] &\implies\quad Q\omega^2\pm\omega_0\omega-Q\omega_0^2=0 \\ &\implies\quad \omega=\frac{\pm\omega_0\pm\sqrt{\omega_0^2+4Q^2\omega_0^2}}{2Q} =\frac{\omega_0}{2Q}\left(\pm 1\pm\sqrt{1+4Q^2}\right). \end{align*}\]

$(d)\;$ We want to find \[\begin{align*} \Arg(V)-\Arg(I) &=\Arg(V/I) \\ &=\Arg(Z(\omega)) \\ &= \arctan\left(Q\left(\dfrac{\omega}{\omega_0}-\dfrac{\omega_0}{\omega}\right)\right). \end{align*}\]

Question 2.30 $\!{}^*\;$ In a particular RLC circuit, the complex impedance $Z$ satisfies \[Z^{-1}=(R+i\omega L)^{-1}+i\omega C\] where the capacitance $C$, inductance $L$ and resistance $R$ are real constants and $\omega$ is the (real-valued) frequency. Show that \[|Z|^2=\frac{R^2+\omega^2L^2}{(1-CL\omega^2)^2+C^2R^2\omega^2}\] and \[\Arg(Z)=\arctan\left[\frac{\omega}{R}\Big(L-C(R^2+\omega^2L^2)\Big)\right].\]

(Hint: make use of $|\alpha/\beta|=|\alpha|/|\beta|$, etc.)

Quick Check

Hint: Use the hint or it’s a mess!

Solution

Tutorial question

\[Z^{-1}=\frac{1}{R+i\omega L}+i\omega C= \frac{1+i\omega C(R+i\omega L)}{R+i\omega L}= \frac{\left(1-\omega^2CL\right)+i\omega CR}{R+i\omega L}\] and taking the reciprocal gives \[Z=\frac{R+i\omega L}{\left(1-\omega^2CL\right)+i\omega CR}.\] Hence, by using $|\alpha/\beta|=|\alpha|/|\beta|$, we get \[|Z|^2=\frac{R^2+\omega^2L^2}{(1-CL\omega^2)^2+C^2R^2\omega^2}.\]

Also, separating $Z^{-1}$ into real and imaginary parts, \[\begin{align*} Z^{-1}=\frac{1}{R+i\omega L}+i\omega C &=\frac{R-i\omega L}{R^2+\omega^2 L^2}+i\omega C \\ &=\frac{R}{R^2+\omega^2 L^2}- i\frac{\omega\left(L-C(R^2+\omega^2 L^2)\right)}{R^2+\omega^2 L^2}. \end{align*}\] Now using $\Arg(Z)=-\Arg(Z^{-1})$ gives the required result.