Topic 3 - Vectors

Week 7 Material

Question 3.1 $\;$ For the vectors \[{\bf a}=4{\bf i}+3{\bf j}+{\bf k},\quad {\bf b}={\bf i}-{\bf j},\quad {\bf c}=5{\bf k},\quad {\bf d}=2{\bf i}+{\bf j}+7{\bf k} \] (where ${\bf i}$, ${\bf j}$, ${\bf k}$ are the standard basis vectors), calculate the following in terms of ${\bf i}$, ${\bf j}$, ${\bf k}$.

$\;\;(a)\;\;{\bf a}+{\bf b}, \hspace{1.4cm}$ $\;\;(b)\;\;{\bf b}+{\bf c},\hspace{1.3cm}$ $\;\;(c)\;\;{\bf d}+{\bf a},\hspace{1.4cm}$ $\;\;(d)\;\;2{\bf a}+3{\bf b},\hspace{1cm}$

$\;\;(e)\;\;2{\bf b}+3{\bf c},\hspace{1cm}$ $\;\;(f)\;\;2{\bf d}-{\bf a},\hspace{0.9cm}$ $\;\;(g)\;\;4{\bf c}-5{\bf b},\hspace{0.9cm}$ $\;\;(h)\;\;{\bf a}-{\bf b}+{\bf c}-2{\bf d}.$

Quick Check

$\;(a)\quad 5{\bf i}+2{\bf j}+{\bf k}.$ $\hspace{1cm}$ $\;(b)\quad {\bf i}-{\bf j}+5{\bf k}.$ $\hspace{1cm}$ $\;(c)\quad 6{\bf i}+4{\bf j}+8{\bf k}.$ $\hspace{1cm}$ $\;(d)\quad 11{\bf i}+3{\bf j}+2{\bf k}.$

$\;(e)\quad 2{\bf i}-2{\bf j}+15{\bf k}.$ $\hspace{1cm}$ $\;(f)\quad -{\bf j}+13{\bf k}.$ $\hspace{1cm}$ $\;(g)\quad -5{\bf i}+5{\bf j}+20{\bf k}.$ $\hspace{1cm}$ $\;(h)\quad -{\bf i}+2{\bf j}-8{\bf k}.$

Solution

$\;(a)\quad {\bf a}+{\bf b}=(4{\bf i}+3{\bf j}+{\bf k})+({\bf i}-{\bf j})=5{\bf i}+2{\bf j}+{\bf k},$

$\;(b)\quad {\bf b}+{\bf c}={\bf i}-{\bf j}+5{\bf k},$

$\;(c)\quad {\bf d}+{\bf a}=(2{\bf i}+{\bf j}+7{\bf k})+(4{\bf i}+3{\bf j}+{\bf k})= 6{\bf i}+4{\bf j}+8{\bf k},$

$\;(d)\quad 2{\bf a}+3{\bf b}=2(4{\bf i}+3{\bf j}+{\bf k})+3({\bf i}-{\bf j})=11{\bf i}+3{\bf j}+2{\bf k},$

$\;(e)\quad 2{\bf b}+3{\bf c}=2({\bf i}-{\bf j})+3(5{\bf k})=2{\bf i}-2{\bf j}+15{\bf k},$

$\;(f)\quad 2{\bf d}-{\bf a}=2(2{\bf i}+{\bf j}+7{\bf k})-(4{\bf i}+3{\bf j}+{\bf k})=-{\bf j}+13{\bf k},$

$\;(g)\quad 4{\bf c}-5{\bf b}=4(5{\bf k})-5({\bf i}-{\bf j})=-5{\bf i}+5{\bf j}+20{\bf k},$

$\;(h)\quad {\bf a}-{\bf b}+{\bf c}-2{\bf d}=(4{\bf i}+3{\bf j}+{\bf k})-({\bf i}-{\bf j})+(5{\bf k})-2(2{\bf i}+{\bf j}+7{\bf k})=-{\bf i}+2{\bf j}-8{\bf k}.$

Question 3.2 $\;$ Given the column vectors ${\bf u}=\begin{pmatrix} 1 \\ 0 \\ 1 \end{pmatrix},\; {\bf v}=\begin{pmatrix} 3 \\ 2 \\ 6 \end{pmatrix},\; {\bf w}=\begin{pmatrix} -1 \\ 0 \\ 0 \end{pmatrix},\;$ calculate

$\;\;(a)\;\;{\bf u}+{\bf v},\hspace{1.1cm}$ $\;\;(b)\;\;{\bf u}+{\bf w},\hspace{1.45cm}$ $\;\;(c)\;\;2{\bf u}+3{\bf v},\hspace{1.5cm}$ $\;\;(d)\;\;2{\bf u}-3{\bf v},$

$\;\;(e)\;\;{\bf v}-{\bf w},\hspace{1cm}$ $\;\;(f)\;\;2{\bf v}-3{\bf w},\hspace{1cm}$ $\;\;(g)\;\;{\bf u}+{\bf v}+{\bf w},\hspace{1cm}$ $\;\;(h)\;\;{\bf w}-{\bf v}-2{\bf u}.$

Quick Check

$\;(a)\quad \begin{pmatrix} 4 \\ 2 \\ 7 \end{pmatrix},$ $\hspace{1cm}$ $\;(b)\quad \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix},$ $\hspace{1cm}$ $\;(c)\quad \begin{pmatrix} 11 \\ 6 \\ 20 \end{pmatrix},$ $\hspace{1cm}$ $\;(d)\quad \begin{pmatrix} -7 \\ -6 \\ -16 \end{pmatrix},$

$\;(e)\quad \begin{pmatrix} 4 \\ 2 \\ 6 \end{pmatrix},$ $\hspace{1cm}$ $\;(f)\quad \begin{pmatrix} 9 \\ 4 \\ 12 \end{pmatrix}$, $\hspace{1cm}$ $\;(g)\quad \begin{pmatrix} 3 \\ 2 \\ 7 \end{pmatrix},$ $\hspace{1cm}$ $\;(h)\quad \begin{pmatrix} -6 \\ -2 \\ -8 \end{pmatrix}$.

Solution

$\;(a)\quad {\bf u}+{\bf v} =\begin{pmatrix} 1 \\ 0 \\ 1 \end{pmatrix} +\begin{pmatrix} 3 \\ 2 \\ 6 \end{pmatrix} =\begin{pmatrix} 4 \\ 2 \\ 7 \end{pmatrix},\hspace{1cm}$

$\;(b)\quad {\bf u}+{\bf w} =\begin{pmatrix} 1 \\ 0 \\ 1 \end{pmatrix} +\begin{pmatrix} -1 \\ 0 \\ 0 \end{pmatrix} =\begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix},$

$\;(c)\quad 2{\bf u}+3{\bf v} =2\begin{pmatrix} 1 \\ 0 \\ 1 \end{pmatrix} +3\begin{pmatrix} 3 \\ 2 \\ 6 \end{pmatrix} = \begin{pmatrix} 11 \\ 6 \\ 20 \end{pmatrix},\hspace{1cm}$

$\;(d)\quad 2{\bf u}-3{\bf v} =2\begin{pmatrix} 1 \\ 0 \\ 1 \end{pmatrix} -3\begin{pmatrix} 3 \\ 2 \\ 6 \end{pmatrix} = \begin{pmatrix} -7 \\ -6 \\ -16 \end{pmatrix},$

$\;(e)\quad {\bf v}-{\bf w} =\begin{pmatrix} 3 \\ 2 \\ 6 \end{pmatrix} -\begin{pmatrix} -1 \\ 0 \\ 0 \end{pmatrix} =\begin{pmatrix} 4 \\ 2 \\ 6 \end{pmatrix},\hspace{1cm}$

$\;(f)\quad 2{\bf v}-3{\bf w} =2\begin{pmatrix} 3 \\ 2 \\ 6 \end{pmatrix} -3\begin{pmatrix} -1 \\ 0 \\ 0 \end{pmatrix} =\begin{pmatrix} 9 \\ 4 \\ 12 \end{pmatrix}$,

$\;(g)\quad {\bf u}+{\bf v}+{\bf w} =\begin{pmatrix} 1 \\ 0 \\ 1 \end{pmatrix} +\begin{pmatrix} 3 \\ 2 \\ 6 \end{pmatrix} +\begin{pmatrix} -1 \\ 0 \\ 0 \end{pmatrix} =\begin{pmatrix} 3 \\ 2 \\ 7 \end{pmatrix},\hspace{0.5cm}$

$\;(h)\quad {\bf w}-{\bf v}-2{\bf u} =\begin{pmatrix} -1 \\ 0 \\ 0 \end{pmatrix} -\begin{pmatrix} 3 \\ 2 \\ 6 \end{pmatrix} -2\begin{pmatrix} 1 \\ 0 \\ 1 \end{pmatrix} =\begin{pmatrix} -6 \\ -2 \\ -8 \end{pmatrix}$.

Question 3.3 $\;$ The position vectors of four points $A$, $B$, $C$, $D$ are \[ \overrightarrow{OA}={\bf a},\quad \overrightarrow{OB}={\bf b},\quad \overrightarrow{OC}={\bf a}+2{\bf b},\quad \overrightarrow{OD}=2{\bf a}-3{\bf b}. \] Express the following in terms of ${\bf a}$ and ${\bf b}$:

$\;\;(a)\;\;\overrightarrow{AC},\hspace{1cm}$ $\;\;(b)\;\;\overrightarrow{DB},\hspace{1cm}$ $\;\;(c)\;\;\overrightarrow{BC},\hspace{1cm}$ $\;\;(d)\;\;\overrightarrow{CD}.$

Quick Check

$\;(a)\quad 2{\bf b}$, $\hspace{1cm}$ $\;(b)\quad -2{\bf a}+4{\bf b}$, $\hspace{1cm}$ $\;(c)\quad {\bf a}+{\bf b}$, $\hspace{1cm}$ $\;(d)\quad {\bf a}-5{\bf b}$.

Solution

$\;(a)\quad \overrightarrow{AC}=\overrightarrow{OC}-\overrightarrow{OA} =({\bf a}+2{\bf b})-{\bf a}=2{\bf b}$,

$\;(b)\quad \overrightarrow{DB}=\overrightarrow{OB}-\overrightarrow{OD} ={\bf b}-(2{\bf a}-3{\bf b})=-2{\bf a}+4{\bf b}$,

$\;(c)\quad \overrightarrow{BC}=\overrightarrow{OC}-\overrightarrow{OB} =({\bf a}+{2 \bf b})-{\bf b}={\bf a}+{\bf b}$,

$\;(d)\quad \overrightarrow{CD}=\overrightarrow{OD}-\overrightarrow{OC} =(2{\bf a}-3{\bf b})-({\bf a}+2{\bf b})={\bf a}-5{\bf b}$.

Question 3.4 $\;$ For a triangle $ABC$, let $D$, $E$, $F$ be the midpoints of $BC$, $CA$ and $AB$ respectively.

$\;\;(a)\;\;$ Show that $\overrightarrow{FE}=\frac12\overrightarrow{BC}$.

$\;\;(b)\;\;$ By writing $\overrightarrow{AD}$ as $\overrightarrow{AC}+\frac12\overrightarrow{CB}$, etc., show that $\overrightarrow{AD}+\overrightarrow{BE}+\overrightarrow{CF}={\bf 0}$.

Quick Check

$(a)\;$ Draw a picture.

$(b)\;$ Show $\overrightarrow{AD}=\overrightarrow{AC}+\overrightarrow{EF}$, find similar expressions for $\overrightarrow{BE}$, $\overrightarrow{CF}$ and add.

Solution

Consider the following diagram:

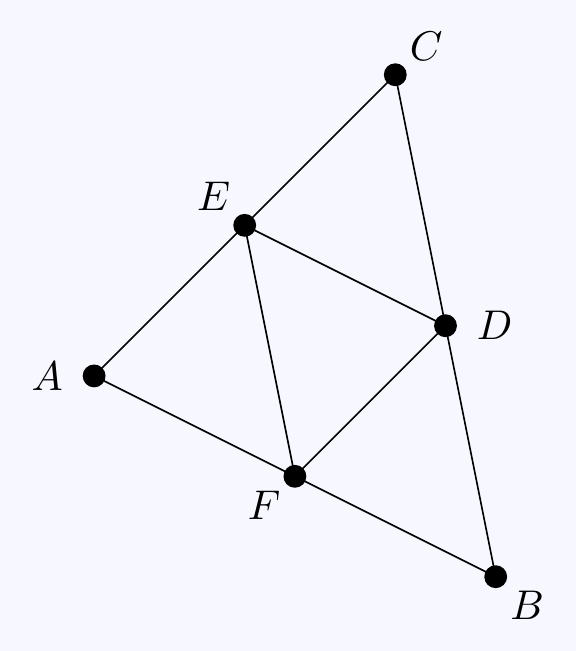
$\;(a)\;$ Since $\overrightarrow{FE}$ and $\overrightarrow{BD}$ are parallel and have the same length, \[\overrightarrow{FE}=\overrightarrow{BD}=\frac12\overrightarrow{BC}.\]

$\;(b)\;$ Using $(a)$, \[\overrightarrow{AD}=\overrightarrow{AC}+\frac12\overrightarrow{CB}= \overrightarrow{AC}+\overrightarrow{EF}.\]

Similarly, using $\overrightarrow{DF}=\frac12\overrightarrow{CA}$, $\overrightarrow{ED}=\frac12\overrightarrow{AB}$, we get \[\begin{align*} \overrightarrow{BE}&=\overrightarrow{BA}+\frac12\overrightarrow{AC}= \overrightarrow{BA}+\overrightarrow{FD}, \\ \overrightarrow{CF}&=\overrightarrow{CB}+\frac12\overrightarrow{BA}= \overrightarrow{CB}+\overrightarrow{DE}. \end{align*}\]

Adding now gives \[\begin{align*} \overrightarrow{AD}+\overrightarrow{BE}+\overrightarrow{CF}&= \left(\overrightarrow{AC}+\overrightarrow{CB}+\overrightarrow{BA}\right)+ \left(\overrightarrow{EF}+\overrightarrow{FD}+\overrightarrow{DE}\right) \\ &=\overrightarrow{AA}+\overrightarrow{EE}=\boldsymbol{0}+\boldsymbol{0}=\boldsymbol{0}. \end{align*}\]

Question 3.5 $\;\;$ Prove that the diagonals of a parallelogram bisect one another.

Quick Check

Hint: follow the same method as the example at the end of Section 3.1 in the notes. In other words, write the vectors from the corners of the parallelogram to the intersection as (unknown) scalar multiples of the diagonals and show these multiples equal $1/2$.

Solution

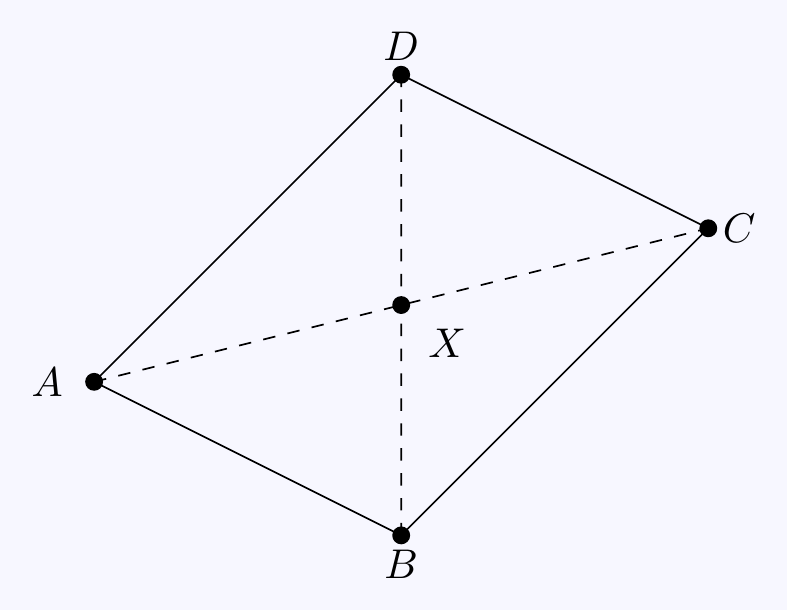
Let $X$ be the intersection of the diagonals. Suppose that $\overrightarrow{AX}=\lambda\overrightarrow{AC}$ and $\overrightarrow{BX}=\mu\overrightarrow{BD}$. We want to show $\lambda=\mu=\frac12$. Now \[\overrightarrow{AX}=\lambda\overrightarrow{AC}=\lambda\left(\overrightarrow{AB}+\overrightarrow{AD}\right)\] and \[\begin{align*} \overrightarrow{AX}=\overrightarrow{AB}+\overrightarrow{BX}&=\overrightarrow{AB}+\mu\overrightarrow{BD} \\ &=\overrightarrow{AB}+\mu\left(\overrightarrow{AD}-\overrightarrow{AB}\right). \end{align*}\]

So \[\lambda\left(\overrightarrow{AB}+\overrightarrow{AD}\right) =\overrightarrow{AB}+\mu\left(\overrightarrow{AD}-\overrightarrow{AB}\right) \] \[\quad\implies\quad (\lambda-\mu)\overrightarrow{AD}=(1-\lambda-\mu)\overrightarrow{AB}.\] However, $\overrightarrow{AB}$ and $\overrightarrow{AD}$ are not parallel (as otherwise it’s not really a parallelogram) hence they can’t be non-zero multiples of each other. Thus \[\left\{\begin{matrix} \lambda-\mu=0 \\ 1-\lambda-\mu=0 \end{matrix}\right. \quad\implies\quad \lambda=\mu=\frac12.\]

Question 3.6 $\;$ The velocity of a boat relative to the water is $3{\bf i}+5{\bf j}$ and that of the water relative to the Earth is ${\bf i}-3{\bf j}$. What is the velocity of the boat relative to the Earth?

Quick Check

The relative velocity is $4{\bf i}+2{\bf j}.$

Solution

The velocity of the boat relative to the water is the velocity of the boat relative to the land minus the velocity of the water relative to the land. We just have to add the two velocities and get \[{\bf v}+{\bf w}=4{\bf i}+2{\bf j}.\]

Question 3.7 $\;$ A meteorologist travelling West at $8\,\textsf{km}\,\textsf{h}^{-1}$ finds that the wind seems to blow directly from the South. On doubling their velocity, they find that it appears to come from the South West. Find the velocity of the wind.

Quick Check

The velocity is $-8{\bf i}+8{\bf j}$.

Solution

Initially, the meteorologists velocity is $-8{\bf i}$ and then it doubles to $-16{\bf i}$. Suppose the wind velocity is ${\bf v}$. We are told that \[-8{\bf i}-{\bf v}=\lambda{\bf j} \qquad\text{and}\qquad -16{\bf i}-{\bf v}=\mu({\bf i}+{\bf j})\] for some $\lambda$ and $\mu$. Hence \[{\bf v}=-8{\bf i}-\lambda{\bf j}=(-\mu-16){\bf i}-\mu{\bf j}.\] Comparing the coefficients of ${\bf i}$ and ${\bf j}$ shows $\mu=-8$ and $\lambda=\mu$. Hence ${\bf v}=-8{\bf i}+8{\bf j}$.

Question 3.8 $\;$ A particle at the corner of a cube is acted on by forces of $1, 2, 3$ Newtons respectively along the diagonals of the faces of the cube which meet at the particle. Find the magnitude of the resultant force acting on the particle. (The “resultant force” just means the vector sum of the individual forces.)

Quick Check

The force is $5$ Newtons.

Solution

The total force is \[{\bf F}=1\left(\frac{{\bf i}+{\bf j}}{\sqrt2}\right) +2\left(\frac{{\bf j}+{\bf k}}{\sqrt2}\right) +3\left(\frac{{\bf k}+{\bf i}}{\sqrt2}\right) =\frac{1}{\sqrt2}\left(4{\bf i}+3{\bf j}+5{\bf k}\right)\] and so $|{\bf F}|=5$ Newtons.

Question 3.9 $\;$ For the following subsets of $\mathbb{R}^2$,

$\;\;(a)\;\;S=\left\{\begin{pmatrix} 1 \\ 2 \end{pmatrix}, \begin{pmatrix} 3 \\ 1 \end{pmatrix} \right\},\hspace{1.3cm}$ $\;\;(b)\;\;S=\left\{\begin{pmatrix} 1 \\ 2 \end{pmatrix}, \begin{pmatrix} 3 \\ 1 \end{pmatrix}, \begin{pmatrix} 0 \\ 0 \end{pmatrix} \right\},$

$\;\;(c)\;\;S=\left\{\begin{pmatrix} 1 \\ 2 \end{pmatrix}, \begin{pmatrix} -3 \\ -6 \end{pmatrix} \right\},\hspace{1cm}$ $\;\;(d)\;\;S=\left\{\begin{pmatrix} 1 \\ 2 \end{pmatrix}, \begin{pmatrix} -3 \\ -6 \end{pmatrix}, \begin{pmatrix} 4 \\ 8 \end{pmatrix}\right\},$

determine if $S$: (i) is linearly independent, (ii) spans $\mathbb{R}^2$, (iii) is a basis of $\mathbb{R}^2$.

Justify your answers.

Quick Check

$(a)\;$ $S$ is linearly independent, it does span $\mathbb{R}^2$, and is a basis.

$(b)\;$ $S$ is not linearly independent, it does span $\mathbb{R}^2$, and is not a basis.

$(c)\;$ $S$ is not linearly independent, it doesn’t span $\mathbb{R}^2$, and is not a basis.

$(d)\;$ $S$ is not linearly independent, it does not span $\mathbb{R}^2$, and is not a basis.

Solution

$(a)\;(i)\;$ To check linear independence, notice \[\lambda_1\begin{pmatrix} 1 \\ 2 \end{pmatrix} +\lambda_2\begin{pmatrix} 3 \\ 1 \end{pmatrix} =\begin{pmatrix} 0 \\ 0 \end{pmatrix} \quad\iff\quad \begin{pmatrix} 1 & 2 \\ 3 & 1 \end{pmatrix} \begin{pmatrix} \lambda_1 \\ \lambda_2 \end{pmatrix} =\begin{pmatrix} 0 \\ 0 \end{pmatrix}. \] Since $\;\begin{vmatrix} 1 & 2 \\ 3 & 1 \end{vmatrix}=-5\neq 0\;$, there is a unique solution which must be $\begin{pmatrix} \lambda_1 \\ \lambda_2 \end{pmatrix}=\begin{pmatrix} 0 \\ 0 \end{pmatrix}$.

Hence this set $S$ is linearly independent.

$\;(a)\;(ii)\;$ To check spanning, it’s almost the same: \[\lambda_1\begin{pmatrix} 1 \\ 2 \end{pmatrix} +\lambda_2\begin{pmatrix} 3 \\ 1 \end{pmatrix} =\begin{pmatrix} a \\ b \end{pmatrix} \quad\iff\quad \begin{pmatrix} 1 & 2 \\ 3 & 1 \end{pmatrix} \begin{pmatrix} \lambda_1 \\ \lambda_2 \end{pmatrix} =\begin{pmatrix} a \\ b \end{pmatrix} \] Again, $\;\begin{vmatrix} 1 & 2 \\ 3 & 1 \end{vmatrix}=-5\neq 0\;$, so there is a (unique) solution $\begin{pmatrix} \lambda_1 \\ \lambda_2 \end{pmatrix}$.

Hence this set $S$ does span $\mathbb{R}^2$.

$\;(a)\;(iii)\;$ Finally, since $S$ is linearly independent and spans, it is a basis.

For this set $S$, there are exactly 2 vectors in 2 dimensions, so all we needed actually needed to do was check the determinant to answer all three parts at once.

(b)$\;\;$ There are 3 vectors in 2 dimensions and so $(i)$ the set is not linearly independent and $(iii)$ it is not a basis. You could alternatively notice any set containing the zero vector cannot be linearly independent - there is automatically a non-trivial linear relation e.g. \[0\begin{pmatrix} 1 \\ 2 \end{pmatrix} +0\begin{pmatrix} 3 \\ 1 \end{pmatrix} +7\begin{pmatrix} 0 \\ 0 \end{pmatrix} =\begin{pmatrix} 0 \\ 0 \end{pmatrix}\]

To check spanning, notice including an extra vector doesn’t make the span any smaller. Hence by part (a), the set does span $\mathbb{R}^2$.

$\;(c)\;$ For two vectors in 2 dimensions, we just need to check the determinant $\;\begin{vmatrix} 1 & 2 \\ -3 & -6 \end{vmatrix}=0.$

This shows $(i)$ $S$ isn’t linearly independent, $(ii)$ doesn’t span and $(iii)$ is not a basis.

$\;(d)\;$ There are 3 vectors in 2 dimensions and so the set is $(i)$ not linearly independent and $(iii)$ is not a basis.

They also don’t span $\mathbb{R}^2$. Any linear combination is actually just a multiple of a single vector \[\lambda_1\begin{pmatrix} 1 \\ 2 \end{pmatrix} +\lambda_2\begin{pmatrix} -3 \\ -6 \end{pmatrix} +\lambda_3\begin{pmatrix} 4 \\ 8 \end{pmatrix} =(\lambda_1-3\lambda_2+4\lambda_3)\begin{pmatrix} 1 \\ 2 \end{pmatrix}\] and so the span of $S$ doesn’t include e.g. $\begin{pmatrix} 1 \\ 0 \end{pmatrix}$.

Question 3.10 $\;$ For the following subsets of $\mathbb{R}^3$,

$\;\;(a)\;\;S=\left\{\begin{pmatrix} 1 \\ -2 \\ 3 \end{pmatrix}, \begin{pmatrix} 2 \\ 1 \\ -2 \end{pmatrix}, \begin{pmatrix} 3 \\ -1 \\ 1 \end{pmatrix} \right\},\hspace{0.2cm}$ $\;\;(b)^*\;\; S=\left\{\begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix}, \begin{pmatrix} 2 \\ 1 \\ -2 \end{pmatrix}, \begin{pmatrix} 3 \\ -1 \\ 1 \end{pmatrix} \right\},$

$\;\;(c)\;\;S=\left\{\begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix}, \begin{pmatrix} 2 \\ 1 \\ -2 \end{pmatrix} \right\},\hspace{2.1cm}$ $\;\;(d)^*\;\;S=\left\{\begin{pmatrix} 1 \\ -1 \\ 1 \end{pmatrix}, \begin{pmatrix} 2 \\ 0 \\ 1 \end{pmatrix}, \begin{pmatrix} 0 \\ 2 \\ -1 \end{pmatrix}, \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix} \right\},$

determine if $S$: (i) is linearly independent, (ii) spans $\mathbb{R}^3$, (iii) is a basis of $\mathbb{R}^3$.

Justify your answers.

Quick Check

$\;(a)\;$ $S$ is not linearly independent, it doesn’t span $\mathbb{R}^3$, and is not a basis.

$\;(b)\;$ $S$ is linearly independent, it does span $\mathbb{R}^3$, and is a basis.

$\;(c)\;$ $S$ is linearly independent, it doesn’t span $\mathbb{R}^3$, and is not a basis.

$\;(d)\;$ $S$ is not be linearly independent, it does span $\mathbb{R}^3$, and is not a basis.

Solution

$\;(a)\;$ Since we have three vectors in a 3-dimensional space, the three conditions are equivalent, i.e. they are all true or all false. Furthermore, they are all true exactly when the matrix with $S$ as its columns has non-zero determinant. However, \[\begin{vmatrix} 1 & 2 & 3 \\ -2 & 1 & -1 \\ 3 & -2 & 1 \end{vmatrix} \;\;\overset{C_2-2C_1}{\overset{C_3-3C_1}{\overset{\,}{=}}}\;\; \begin{vmatrix} 1 & 0 & 0 \\ -2 & 5 & 5 \\ 3 & -8 & -8 \end{vmatrix} = \begin{vmatrix} 5 & 5 \\ -8 & -8 \end{vmatrix}=0\] so the set $S$ is not linearly independent or spanning nor a basis.

$\;(b)\;$ Tutorial question

We have three vectors in a 3-dimensional space, so checking the determinant \[\begin{vmatrix} 1 & 2 & 3 \\ 2 & 1 & -1 \\ 3 & -2 & 1 \end{vmatrix} \;\;\overset{C_2-2C_1}{\overset{C_3-3C_1}{\overset{\,}{=}}}\;\; \begin{vmatrix} 1 & 0 & 0 \\ 2 & -3 & -7 \\ 3 & -8 & -8 \end{vmatrix} =\begin{vmatrix} -3 & -7 \\ -8 & -8 \end{vmatrix}=24-56=-32\neq 0\] shows that the set $S$ is linearly independent, it does span and is a basis of $\mathbb{R}^3$.

$\;(c)\;$ With only two vectors in 3-dimensional space, $S$ can not span or be a basis of $\mathbb{R}^3$.

The set is linearly independent however, since the two vectors are not multiples of each other. More explicitly, \[\begin{align*} \lambda_1\begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix}+ \lambda_2\begin{pmatrix} 2 \\ 1 \\ -2 \end{pmatrix}= \begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix} %\quad\implies\quad \begin{cases} \lambda_1+2\lambda_2=0 \\ 2\lambda_1+ \lambda_2=0 \\ 3\lambda_1-2\lambda_2=0 \end{cases} \\ \quad\implies\quad \lambda_1=\lambda_2=0. \end{align*}\]

$\;(d)\;$ Tutorial question

With four vectors in 3-dimensional space, $S$ can not be linearly independent or be a basis.

To check if $S$ spans, it is enough to find three of the four vectors that span. Selecting the last three (after trial and error maybe), we have \[\begin{vmatrix} 2 & 0 & 1 \\ 0 & 2 & 2 \\ 1 & -1 & 3 \end{vmatrix} =2\begin{vmatrix} 2 & 2 \\ -1 & 3 \end{vmatrix} +\begin{vmatrix} 0 & 2 \\ 1 & -1 \end{vmatrix} =2(6+2)+(0-2)=14\neq 0\] In particular, these three vectors span $\mathbb{R}^3$ and so $S$ spans $\mathbb{R}^3$.

Question 3.11 $\!{}^*\;$ For which values of $t\in\mathbb{R}$ is the following set of vectors linearly independent? \[S=\left\{\begin{pmatrix} 2 \\ -3 \\ 4 \end{pmatrix}, \begin{pmatrix} t \\ -2 \\ 2 \end{pmatrix}, \begin{pmatrix} -4 \\ 6 \\ -8 \end{pmatrix} \right\}.\]

Quick Check

$S$ is not linearly independent for any value of $t$.

Solution

Tutorial question

There is a non-trivial linear relation no matter what value $t$ takes. (The first and third vectors are not linearly independent!) \[2\begin{pmatrix} 2 \\ -3 \\ 4 \end{pmatrix} +0\begin{pmatrix} t \\ -2 \\ 2 \end{pmatrix} +\begin{pmatrix} -4 \\ 6 \\ -8 \end{pmatrix} =\begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix}\] so the set $S$ is never linearly independent.

Alternatively, one could check the determinant is zero for all $t\in\mathbb{R}$: \[\begin{vmatrix} 2 & t & -4 \\ -3 & -2 & 6 \\ 4 & 2 & -8 \end{vmatrix}=0.\]

Question 3.12 $\;$ Suppose that ${\bf u}$, ${\bf v}$ and ${\bf w}$ are vectors in $\mathbb{R}^3$. Show that the set $\{{\bf u}, {\bf v}, {\bf w}\}$ is a basis of $\mathbb{R}^3$ if and only if the set $\{{\bf u}+{\bf v}, {\bf v}+{\bf w}, {\bf w}+{\bf u}\}$ is a basis of $\mathbb{R}^3$.

Quick Check

Hint: show that linear combinations of one set are precisely the same vectors as linear combinations of the other set.

Solution

We will show that linear combinations of one set are precisely the same vectors as linear combinations of the other set. Consider \[\lambda_1({\bf u}+{\bf v}) +\lambda_2({\bf v}+{\bf w}) +\lambda_3({\bf w}+{\bf u}) =\mu_1{\bf u}+\mu_2{\bf v}+\mu_3{\bf w}\] Given the $\lambda_i$, we can find the $\mu_i$ using \[\begin{split} \lambda_1+\lambda_3&=\mu_1 \\ \lambda_1+\lambda_2&=\mu_2 \\ \lambda_2+\lambda_3&=\mu_3 \end{split}\quad\implies\quad \begin{pmatrix} 1 & 0 & 1 \\ 1 & 1 & 0 \\ 0 & 1 & 1 \end{pmatrix} \begin{pmatrix} \lambda_1 \\ \lambda_2 \\ \lambda_3 \end{pmatrix} =\begin{pmatrix} \mu_1 \\ \mu_2 \\ \mu_3 \end{pmatrix} \] Furthermore, this matrix is invertible (check it’s determinant is non-zero) and so given the $\mu_i$, we can find the $\lambda_i$. In other words, we can transform between linear combinations of the two sets and so if one is a basis, so is the other.

Question 3.13 $\;$ For the vectors ${\bf a}=4{\bf i}+3{\bf j}+{\bf k}$, ${\bf b}={\bf i}-{\bf j}$, ${\bf c}=5{\bf k}$, ${\bf d}=2{\bf i}+{\bf j}+7{\bf k}$, calculate

$\;\;(a)\;\;{\bf a}\cdot{\bf b}, \hspace{0.7cm}$ $\;\;(b)\;\;{\bf a}\cdot({\bf b}+{\bf c}),\hspace{0.7cm}$ $\;\;(c)\;\;({\bf b}-{\bf a})\cdot({\bf b}+{\bf a}),\hspace{0.5cm}$

$\;\;(d)\;\;|{\bf a}|,\hspace{1.05cm}$ $\;\;(e)\;\;|{\bf b}|,\hspace{2cm}$ $\;\;(f)\;\;|{\bf c}|,\hspace{2.2cm}$ $\;\;(g)\;\;|{\bf d}|.$

Quick Check

$\;(a)\quad 1,$ $\hspace{1cm}$ $\;(b)\quad 6,$ $\hspace{1cm}$ $\;(c)\quad -24,$ $\hspace{1cm}$ $\;(d)\quad \sqrt{26},$

$\;(e)\quad \sqrt2,$ $\hspace{1cm}$ $\;(f)\quad 5,$ $\hspace{1cm}$ $\;(g)\quad \sqrt{54}.$

Solution

$\;(a)\quad {\bf a}\cdot{\bf b}=(4{\bf i}+3{\bf j}+{\bf k})\cdot({\bf i}-{\bf j}) =4\times1+3\times(-1)+1\times 0=1.$

$\;(b)\quad {\bf a}\cdot({\bf b}+{\bf c})=(4{\bf i}+3{\bf j}+{\bf k})\cdot({\bf i}-{\bf j}+5{\bf k}) =4\times 1+3\times(-1)+1\times 5=6.$

$\;(c)\quad ({\bf b}-{\bf a})\cdot({\bf b}+{\bf a})=(-3{\bf i}-4{\bf j}-{\bf k})\cdot(5{\bf i}+2{\bf j}+{\bf k})$

$\hspace{2cm} =(-3)\times5+(-4)\times 2+(-1)\times 1=-24.$

$\;(d)\quad |{\bf a}|=\sqrt{4^2+3^2+1^2}=\sqrt{26}.$

$\;(e)\quad |{\bf b}|=\sqrt{1^2+(-1)^2}=\sqrt2.$

$\;(f)\quad |{\bf c}|=\sqrt{0^2+0^2+5^2}=5.$

$\;(g)\quad |{\bf d}|=\sqrt{2^2+1^2+7^2}=\sqrt{54}.$

Question 3.14 $\;$ For the vectors in the previous question, calculate the cosines of the angles

$\;\;(a)^*\;\;$ between ${\bf a}$ and ${\bf b},\qquad$ $\;\;(b)\;\;$ between ${\bf b}$ and ${\bf c},\qquad$ $\;\;(c)\;\;$ between ${\bf c}$ and ${\bf d}.$

Quick Check

$\;(a)$ $\dfrac{1}{2\sqrt{13}},$ $\hspace{1cm}$ $\;(b)$ $0,$ $\hspace{1cm}$ $\;(c)$ $\dfrac{7}{3\sqrt6}.$

Solution

$\;(a)$ Tutorial question

\[\cos\theta=\frac{{\bf a}\cdot{\bf b}}{|{\bf a}||{\bf b}|}= \frac{4\times 1+3\times(-1)+1\times 0}{\sqrt{4^2+3^2+1^2}\sqrt{1^2+(-1)^2+0^2}}= \frac{1}{\sqrt{52}}=\frac{1}{2\sqrt{13}}.\]

$\;(b)$ \[\cos\theta=\frac{{\bf b}\cdot{\bf c}}{|{\bf b}||{\bf c}|}= \frac{1\times 0+(-1)\times 0+0\times 5}{\sqrt{1^2+(-1)^2+0^2}\sqrt{0^2+0^2+5^2}}=0.\]

$\;(c)$ \[\cos\theta=\frac{{\bf c}\cdot{\bf d}}{|{\bf c}||{\bf d}|}= \frac{0\times 2+0\times 1+5\times 7}{\sqrt{0^2+0^2+5^2}\sqrt{2^2+1^2+7^2}}= \frac{35}{5\sqrt{54}}=\frac{7}{3\sqrt6}.\]

$\;(b)$ \[\cos\theta=\frac{{\bf b}\cdot{\bf c}}{|{\bf b}||{\bf c}|}= \frac{1\times 0+(-1)\times 0+0\times 5}{\sqrt{1^2+(-1)^2+0^2}\sqrt{0^2+0^2+5^2}}=0.\]

$\;(c)$ \[\cos\theta=\frac{{\bf c}\cdot{\bf d}}{|{\bf c}||{\bf d}|}= \frac{0\times 2+0\times 1+5\times 7}{\sqrt{0^2+0^2+5^2}\sqrt{2^2+1^2+7^2}}= \frac{35}{5\sqrt{54}}=\frac{7}{3\sqrt6}.\]

Question 3.15 $\;$ Find unit vectors along the directions of ${\bf u}=\begin{pmatrix} 1 \\ 0 \\ 1 \end{pmatrix}, {\bf v}=\begin{pmatrix} 3 \\ 2 \\ 6 \end{pmatrix}$ and ${\bf w}=\begin{pmatrix} -1 \\ 0 \\ 0 \end{pmatrix}.$

Quick Check

We just need to divide each vector by its length:

$\;(a)\;\;\dfrac{1}{\sqrt2}\begin{pmatrix} 1 \\ 0 \\ 1 \end{pmatrix},\hspace{1cm}$ $\;(b)\;\;\dfrac{1}{7}\begin{pmatrix} 3 \\ 2 \\ 6 \end{pmatrix},\hspace{1cm}$ $\;(c)\;\;\begin{pmatrix} -1 \\ 0 \\ 0 \end{pmatrix}$.

Solution

We just need to divide each vector by its length:

$\;(a)\;\;\hat{{\bf u}}=\dfrac{{\bf u}}{|{\bf u}|} =\dfrac{1}{\sqrt2}\begin{pmatrix} 1 \\ 0 \\ 1 \end{pmatrix},\hspace{0.5cm}$ $\;(b)\;\;\hat{{\bf v}}=\dfrac{{\bf v}}{|{\bf v}|} =\dfrac{1}{7}\begin{pmatrix} 3 \\ 2 \\ 6 \end{pmatrix},\hspace{0.5cm}$ $\;(c)\;\;\hat{{\bf w}}=\dfrac{{\bf w}}{|{\bf w}|} =\begin{pmatrix} -1 \\ 0 \\ 0 \end{pmatrix}$.

Question 3.16 $\;\;$ Find the angles and side lengths of the triangle whose vertices have position vectors \[{\bf i}+{\bf j}+{\bf k},\quad 2{\bf i}-{\bf j}-{\bf k},\quad -{\bf i}+{\bf j}-{\bf k}.\]

Quick Check

The lengths are $3$, $\sqrt{13}$, $2\sqrt2.$

The angles are $\arccos\left(\frac{-7}{3\sqrt{13}}\right),$ $\arccos\left(-\frac{3}{\sqrt{26}}\right),$ $\arccos\left(-\frac{1}{3\sqrt2}\right)$.

Solution

The edges of the triangle have vectors \[\begin{align*} {\bf u}&=(2{\bf i}-{\bf j}-{\bf k})-({\bf i}+{\bf j}+{\bf k})={\bf i}-2{\bf j}-2{\bf k}, \\ {\bf v}&=(-{\bf i}+{\bf j}-{\bf k})-(2{\bf i}-{\bf j}-{\bf k})=-3{\bf i}+2{\bf j}, \\ {\bf w}&=({\bf i}+{\bf j}+{\bf k})-(-{\bf i}+{\bf j}-{\bf k})=2{\bf i}+2{\bf k}. \end{align*}\] The lengths are \[|{\bf u}|=\sqrt9=3, \qquad |{\bf v}|=\sqrt{13}, \qquad |{\bf w}|=\sqrt8=2\sqrt2,\] and the angles are \[\begin{align*} \arccos\left(\frac{{\bf u}\cdot{\bf v}}{|{\bf u}||{\bf v}|}\right)&=\arccos\left(\frac{-7}{3\sqrt{13}}\right), \\ \arccos\left(\frac{{\bf v}\cdot{\bf w}}{|{\bf v}||{\bf w}|}\right)&=\arccos\left(\frac{-6}{2\sqrt{26}}\right) =\arccos\left(-\frac{3}{\sqrt{26}}\right), \\ \arccos\left(\frac{{\bf w}\cdot{\bf u}}{|{\bf w}||{\bf u}|}\right)&=\arccos\left(\frac{-2}{6\sqrt2}\right) =\arccos\left(-\frac{1}{3\sqrt2}\right). \end{align*}\]

Week 8 Material

Question 3.17 $\;$ For the vectors ${\bf u}=\begin{pmatrix} 1\\0\\1 \end{pmatrix}$ and ${\bf v}=\begin{pmatrix} 3\\2\\6 \end{pmatrix}$, find

$\;\;(a)\;\;$ the projection of ${\bf u}$ onto ${\bf v}$,

$\;\;(b)^*\;\;$ the projection of ${\bf v}$ onto ${\bf u}$.

Quick Check

$(a)\;$ $\dfrac{9}{49}\begin{pmatrix} 3 \\ 2 \\ 6 \end{pmatrix}.$ $\hspace{1cm}$ $(b)\;$ $\dfrac92\begin{pmatrix} 1 \\ 0 \\ 1 \end{pmatrix}.$

Solution

$(a)\;$ The projection of ${\bf u}$ onto ${\bf v}$ is \[\left(\frac{{\bf u}\cdot{\bf v}}{{\bf v}\cdot{\bf v}}\right){\bf v}= \frac{3+0+6}{9+4+36}\begin{pmatrix} 3 \\ 2 \\ 6 \end{pmatrix} =\frac{9}{49}\begin{pmatrix} 3 \\ 2 \\ 6 \end{pmatrix}.\]

$(b)\;$ Tutorial question

The projection of ${\bf v}$ onto ${\bf u}$ is \[\left(\frac{{\bf v}\cdot{\bf u}}{{\bf u}\cdot{\bf u}}\right){\bf u}= \frac{3+0+6}{1+0+1}\begin{pmatrix} 1 \\ 0 \\ 1 \end{pmatrix} =\frac92\begin{pmatrix} 1 \\ 0 \\ 1 \end{pmatrix}.\]

Question 3.18 $\;$ Given a non-zero vector ${\bf b}$, show that any vector ${\bf a}$ can be written in a unique way as the sum of a vector ${\bf a}_{\parallel}$ parallel to ${\bf b}$ and a vector ${\bf a}_{\perp}$ perpendicular to ${\bf b}$.

Quick Check

Hint: consider the projection of ${\bf a}$ onto ${\bf b}$ and the non-projected part of ${\bf a}$.

Solution

Let ${\bf a}_{\parallel}$ be the projection of ${\bf a}$ onto ${\bf b}$ and let ${\bf a}_{\perp}$ be what’s left, i.e. set \[{\bf a}_{\parallel}=\left(\frac{{\bf a}\cdot{\bf b}}{|{\bf b}|^2}\right){\bf b} \qquad\text{and}\qquad {\bf a}_{\perp}={\bf a}-\left(\frac{{\bf a}\cdot{\bf b}}{|{\bf b}|^2}\right){\bf b}. \] Then clearly ${\bf a}_{\parallel}$ is parallel to ${\bf b}$ and \[{\bf a}_{\perp}\cdot{\bf b}= {\bf a}\cdot{\bf b}-\left(\frac{{\bf a}\cdot{\bf b}}{|{\bf b}|^2}\right){\bf b}\cdot{\bf b}=0,\] so ${\bf a}_{\perp}$ is perpendicular to ${\bf b}$.

To see why this is the only way, suppose ${\bf a}={\bf u}+{\bf v}$ where ${\bf u}$ is parallel to ${\bf b}$ and ${\bf v}$ is perpendicular to ${\bf b}$. Then ${\bf a}={\bf u}+{\bf v}={\bf a}_{\parallel}+{\bf a}_{\perp}$ where ${\bf a}_{\parallel}$ and ${\bf a}_{\perp}$ are defined as above, so \[{\bf u}-{\bf a}_{\parallel}={\bf a}_{\perp}-{\bf v}.\] The left and right hand sides are vectors with different directions so must be zero, hence we must have ${\bf u}={\bf a}_{\parallel}$ and ${\bf v}={\bf a}_{\perp}$.

Question 3.19 $\;$ A constant force represented by the vector ${{\bf F}}=3{\bf i}+2{\bf j}+{\bf k}$ acts on a particle as it is displaced through the vector ${\bf d}={\bf i}+2{\bf j}$. Find the work done by the force.

Quick Check

The work done equals $7$ (in appropriate units).

Solution

The work done is just ${\bf F}\cdot{\bf d}=3(1)+2(2)+1(0)=7$. (Yes, it’s that easy…)

Question 3.20 $\;$ Constant forces of magnitudes 4, 2, and 1 Newtons act on a single particle in the directions of the vectors $6{\bf i}+2{\bf j}+3{\bf k}$, $3{\bf i}-2{\bf j}+6{\bf k}$, and $2{\bf i}-3{\bf j}-6{\bf k}$ respectively. Find the work done as the particle is moved from the point $(2,-1,-3)$ to $(5,-1,1)$, where the units of distance are metres.

Quick Check

The work done is $24\,\textsf{J}.$

Solution

The three forces are \[\begin{align*} {\bf F}_1&=4\left(\frac{6{\bf i}+2{\bf j}+3{\bf k}}{\sqrt{6^2+2^2+3^2}}\right) =\frac47(6{\bf i}+2{\bf j}+3{\bf k}), \\ {\bf F}_2&=2\left(\frac{3{\bf i}-2{\bf j}+6{\bf k}}{\sqrt{3^2+2^2+6^2}}\right) =\frac27(3{\bf i}-2{\bf j}+6{\bf k}), \\ {\bf F}_3&=1\left(\frac{2{\bf i}-3{\bf j}-6{\bf k}}{\sqrt{2^2+3^2+6^2}}\right) =\frac17(2{\bf i}-3{\bf j}-6{\bf k}), \end{align*}\] so the total force is ${\bf F}={\bf F}_1+{\bf F}_2+{\bf F}_3=\frac17(32{\bf i}+{\bf j}+18{\bf k})$.

The displacement is ${\bf d}=3{\bf i}+4{\bf k}$ so the work done is \[{\bf F}\cdot{\bf d}=\frac17(32\times 3+1\times 0+18\times 4)=24\;\textsf{J}.\] [Recall that work has units of energy measured in Joules.]

Question 3.21 $\;$ If the sum of two forces is equal in magnitude to one of them and perpendicular to it in direction, find the magnitude of the other force and the angle between the two forces.

Quick Check

Show that $|{\bf F}_2|=\sqrt{2}|{\bf F}_1|$ and the angle between the forces is $\theta=\frac{3\pi}{4}.$

Solution

Let the two forces be ${\bf F}_1$, ${\bf F}_2$ and choose orthonormal basis $\{{\bf i},{\bf j}\}$ so that ${\bf F}_1$ is in direction ${\bf i}$ and ${\bf F}_1+{\bf F}_2$ is in direction ${\bf j}$. Then \[{\bf F}_1=|{\bf F}_1|\,{\bf i} \qquad\text{and}\qquad {\bf F}_1+{\bf F}_2=|{\bf F}_1+{\bf F}_2|\,{\bf j}=|{\bf F}_1|\,{\bf j}\] since we are told that ${\bf F}_1+{\bf F}_2$ has the same magnitude as ${\bf F}_1$. Thus \[{\bf F}_2=|{\bf F}_1|\,({\bf j}-{\bf i}) \qquad\implies\qquad |{\bf F}_2|=\sqrt{2}|{\bf F}_1|.\] Also, if $\theta$ is the angle between the forces, \[\cos\theta=\frac{{\bf F}_1\cdot{\bf F}_2}{|{\bf F}_1|\,|{\bf F}_2|} =\frac{|{\bf F}_1|^2\,{\bf i}\cdot({\bf j}-{\bf i})}{\sqrt2|{\bf F}_1|^2}=-\frac{1}{\sqrt2} \qquad\implies\qquad \theta=\frac{3\pi}{4}.\]

Question 3.22 $\;$ Find parametric and Cartesian equations of the straight lines

$\;\;(a)\;\;$ through the point $(1,2,3)$ and parallel to $(5,6,2)$,

$\;\;(b)\;\;$ through the point $(1,0,1)$ and parallel to $(4,3,5)$,

$\;\;(c)\;\;$ through the points $(1,1,1)$ and $(2,5,3)$,

$\;\;(d)\;\;$ through the points $(0,0,0)$ and $(2,1,0)$.

Quick Check

$(a)\;$ Parametric: $\;\;{\bf x} = \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix} + t\begin{pmatrix} 5 \\ 6 \\ 2 \end{pmatrix}\;\;$ and Cartesian: $\;\;\dfrac{x-1}{5} = \dfrac{y-2}{6} = \dfrac{z-3}{2}.$

$(b)\;$ Parametric: $\;\;{\bf x}=\begin{pmatrix} 1\\0\\1 \end{pmatrix} + t\begin{pmatrix} 4\\3\\5 \end{pmatrix}\;\;$ and Cartesian: $\;\;\dfrac{x-1}{4} = \dfrac{y}{3} = \dfrac{z-1}{5}$.

$(c)\;$ Parametric: $\;\;{\bf x} = \begin{pmatrix} 1\\1\\1 \end{pmatrix} + t\begin{pmatrix} 1\\4\\2 \end{pmatrix}\;\;$ and Cartesian: $\;\;\dfrac{x-1}{1} = \dfrac{y-1}{4} = \dfrac{z-1}{2}.$

$(d)\;$ Parametric: $\;\;{\bf x} = \begin{pmatrix} 0\\0\\0 \end{pmatrix} + t\begin{pmatrix} 2\\1\\0 \end{pmatrix}\;\;$ and Cartesian: $\;\;\dfrac{x}{2} = \dfrac{y}{1}$ and $z=0.$

Solution

$(a)\;$ The parametric equation is ${\bf x}={\bf a} + t{\bf d}$ where ${\bf a}$ is a point on the line and ${\bf d}$ is the direction vector of the line. So here \[ {\bf x} = \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix} + t\begin{pmatrix} 5 \\ 6 \\ 2 \end{pmatrix}. \] The Cartesian equations are given by eliminating $t$ so that \[ \frac{x-1}{5} = \frac{y-2}{6} = \frac{z-3}{2}. \]

$(b)\;$ Here $\displaystyle {\bf x}=\begin{pmatrix} 1\\0\\1 \end{pmatrix} + t\begin{pmatrix} 4\\3\\5 \end{pmatrix}$ and the equations are $\displaystyle \frac{x-1}{4} = \frac{y}{3} = \frac{z-1}{5}$.

$(c)\;$ This time we need to first calculate the direction vector \[{\bf d}=\begin{pmatrix} 2\\5\\3 \end{pmatrix} - \begin{pmatrix} 1\\1\\1 \end{pmatrix} = \begin{pmatrix} 1\\4\\2 \end{pmatrix},\] so then \[ {\bf x} = \begin{pmatrix} 1\\1\\1 \end{pmatrix} + t\begin{pmatrix} 1\\4\\2 \end{pmatrix} \qquad\text{and}\qquad x-1 = \frac{y-1}{4} = \frac{z-1}{2}. \]

$(d)\;$ The direction vector is ${\bf d}=\begin{pmatrix} 2\\1\\0 \end{pmatrix} - \begin{pmatrix} 0\\0\\0 \end{pmatrix} = \begin{pmatrix} 2\\1\\0 \end{pmatrix}$, so then \[ {\bf x} = \begin{pmatrix} 0\\0\\0 \end{pmatrix} + t\begin{pmatrix} 2\\1\\0 \end{pmatrix} \qquad\text{and}\qquad \frac{x}{2} = \frac{y}{1}. \] Here we cannot re-arrange the $z$ equation for $t$. However, we clearly have $z=0$ and so the Cartesian equations for the line are \[\frac{x}{2} = \frac{y}{1}\quad\text{and}\quad z=0.\]

Question 3.23 $\!{}^*\;$ Find the value of $c$ so that the point $(4, 10, c)$ lies on the straight line that passes through the points $(-2,0,3 )$ and $(1,5,6)$.

Quick Check

Show that $c = 9.$

Solution

Tutorial question

First we find a parametric equation for the line. A direction vector is \[ {\bf d}=\begin{pmatrix} 1\\5\\6 \end{pmatrix} - \begin{pmatrix} -2\\0\\3 \end{pmatrix} = \begin{pmatrix} 3\\5\\3 \end{pmatrix}, \] so a parametric equation of the line is \[ {\bf x} = \begin{pmatrix} -2\\0\\3 \end{pmatrix} + t\begin{pmatrix} 3\\5\\3 \end{pmatrix}. \] We then look for the value of $t$ corresponding to the first two coordinates of our point, which are $x=4$ and $y=10$. These give \[ x+2 = 3t \quad \implies t=2 \qquad\text{and}\qquad y=5t \quad\implies t=2. \] Both give the same value of $t$, so these $x$ and $y$ coordinates are consistent with the line. From $z=3+3t$ we then find $c = 3 + 3(2) = 9.$

Question 3.24 $\!{}^*\;$ Find the angle between the normals to the planes $x+y=1$ and $y+z=2$.

Quick Check

The angle is $\pi/3.$

Solution

Tutorial question

The normals to the planes are ${\bf n}_1=\begin{pmatrix} 1 \\ 1 \\ 0 \end{pmatrix}$ and ${\bf n}_2=\begin{pmatrix} 0 \\ 1 \\ 1 \end{pmatrix}$. The angle $\theta$ between these satisfies \[\cos\theta=\frac{{\bf n}_1\cdot{\bf n}_2}{|{\bf n}_1||{\bf n}_2|}= \frac{1}{\sqrt2.\sqrt2}=\frac12 \quad\implies\quad \theta=\frac{\pi}{3}.\]

Question 3.25 $\;$ Find a Cartesian equation of a plane passing through $(1,1,1)$, given that a normal vector to the plane makes angles $\pi/3$, $\pi/4$, $\pi/3$ with ${\bf i}$, ${\bf j}$, ${\bf k}$ respectively.

Quick Check

The equation of the plane is $x+\sqrt2y+z=2+\sqrt2.$

Solution

Let ${\bf n}=\begin{pmatrix} n_1 \\ n_2 \\ n_3 \end{pmatrix}$ be the unit length normal to the plane. It satisfies \[\begin{align*} {\bf n}\cdot{\bf i} &=n_1=\cos(\pi/3)= 1/2,\\ {\bf n}\cdot{\bf j} &=n_2=\cos(\pi/4)= 1/\sqrt2, \\ {\bf n}\cdot{\bf k} &=n_3=\cos(\pi/3)= 1/2. \end{align*}\] The plane is thus $({\bf x}-{\bf a})\cdot{\bf n}=0$, i.e. \[\begin{pmatrix} x-1 \\ y-1 \\ z-1 \end{pmatrix}\cdot \begin{pmatrix} 1/2 \\ 1/\sqrt2 \\ 1/2 \end{pmatrix}=0 \qquad\implies\qquad x+\sqrt2y+z=2+\sqrt2.\]

Question 3.26 $\;$ Find a Cartesian equation of a plane perpendicular to the line passing through the points $(1,2,3)$ and $(2,4,12)$, given that the plane passes through $(2,3,-7)$.

Quick Check

The equation of the plane is $x+2y+9z=-55.$

Solution

The normal to the plane is \[{\bf n}=\begin{pmatrix} 2 \\ 4 \\ 12 \end{pmatrix}- \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix}= \begin{pmatrix} 1 \\ 2 \\ 9 \end{pmatrix}\] so the parametric equation is $({\bf x}-{\bf a})\cdot{\bf n}=0$, i.e. \[\begin{pmatrix} x-2 \\ y-3 \\ z+7 \end{pmatrix}\cdot\begin{pmatrix} 1 \\ 2 \\ 9 \end{pmatrix}=0 \quad\implies\quad x+2y+9z=-55.\]

Question 3.27 $\!{}^*\;$ Find a Cartesian equation of the plane that passes through $(1,2,3)$ and is parallel to the plane $3x-y+2z=4$. What is the shortest distance between the two planes?

Quick Check

The equation of the plane is $3x-y+2z=7$ and the shortest distance is $\dfrac{3\sqrt{14}}{14}.$

Solution

Tutorial question

The normal to the plane is the same as that of $3x-y+2z=4$ since they are parallel, and so we may take ${\bf n}=\begin{pmatrix} 3 \\ -1 \\ 2 \end{pmatrix}$.

Furthermore, it passes through ${\bf a}=\begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix}$ so has equation $({\bf x}-{\bf a})\cdot{\bf n}=0$, i.e. \[\begin{pmatrix} x-1 \\ y-2 \\ z-3 \end{pmatrix}\cdot \begin{pmatrix} 3 \\ -1 \\ 2 \end{pmatrix}=0 \quad\implies\quad 3x-y+2z=7.\]

The shortest distance between the planes will be along the direction ${\bf n}$. The line through ${\bf a}$ in direction ${\bf n}$ has parametric form ${\bf x}={\bf a}+t{\bf n}$, that is, \[ \begin{pmatrix} x \\ y \\ z \end{pmatrix}= \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix}+ t\begin{pmatrix} 3 \\ -1 \\ 2 \end{pmatrix} =\begin{pmatrix} 1+3t \\ 2-t \\ 3+2t \end{pmatrix}.\] This line intersects the other plane $3x-y+2z=4$ when \[3(1+3t)-(2-t)+2(3+2t)=4 \quad\implies\quad t=-3/14\] i.e. at ${\bf x}={\bf a}-\dfrac{3}{14}\begin{pmatrix} 3 \\ -1 \\ 2 \end{pmatrix}$. We want the distance from ${\bf a}$ to this point of intersection, which is \[\left|-\dfrac{3}{14}\begin{pmatrix} 3 \\ -1 \\ 2 \end{pmatrix}\right| =\dfrac{3\sqrt{14}}{14}.\]

Week 9 Material

Question 3.28 $\;$ For the vectors \[{\bf a}=4{\bf i}+3{\bf j}+{\bf k},\quad {\bf b}={\bf i}-{\bf j},\quad {\bf c}=5{\bf k},\quad {\bf d}=2{\bf i}+{\bf j}+7{\bf k},\] calculate

$\;\;(a)\;\;{\bf a}\times{\bf b},\hspace{1.85cm}$ $\;\;(b)\;\;{\bf a}\times({\bf b}+{\bf c}),\hspace{1cm}$ $\;\;(c)\;\;({\bf b}-{\bf a})\times({\bf b}+{\bf a}),$

$\;\;(d)\;\;{\bf a}\cdot({\bf b}\times{\bf c}),\hspace{1cm}$ $\;\;(e)\;\;{\bf b}\cdot({\bf c}\times{\bf d}),\hspace{1.15cm}$ $\;\;(f)\;\;{\bf b}\cdot({\bf a}\times{\bf c}).$

Quick Check

$(a)\;$ ${\bf i}+{\bf j}-7{\bf k},$ $\hspace{1cm}$ $(b)\;$ $16{\bf i}-19{\bf j}-7{\bf k},$ $\hspace{1cm}$ $(c)\;$ $-2{\bf i}-2{\bf j}+14{\bf k},$

$(d)\;$ $-35,$ $\hspace{1cm}$ $(e)\;$ $-15,$ $\hspace{1cm}$ $(f)\;$ $35.$

Solution

$(a)\;$ \[\begin{align*} {\bf a}\times{\bf b}&= \begin{vmatrix} {\bf i} & {\bf j} & {\bf k} \\ 4 & 3 & 1 \\ 1 & -1 & 0 \end{vmatrix} \\ &={\bf i}(0+1) -{\bf j}(0-1) +{\bf k}(-4-3) \\ &={\bf i}+{\bf j}-7{\bf k}. \end{align*}\]

$(b)\;$ \[\begin{align*} {\bf a}\times({\bf b}+{\bf c})&= \begin{vmatrix} {\bf i} & {\bf j} & {\bf k} \\ 4 & 3 & 1 \\ 1 & -1 & 5 \end{vmatrix} \\ &={\bf i}(15+1) -{\bf j}(20-1) +{\bf k}(-4-3) \\ &=16{\bf i}-19{\bf j}-7{\bf k}. \end{align*}\]

$(c)\;$ \[\begin{align*} ({\bf b}-{\bf a})\times({\bf b}+{\bf a})&= \begin{vmatrix} {\bf i} & {\bf j} & {\bf k} \\ -3 & -4 & -1 \\ 5 & 2 & 1 \end{vmatrix} \\ &={\bf i}(-4+2) -{\bf j}(-3+5) +{\bf k}(-6+20) \\ &=-2{\bf i}-2{\bf j}+14{\bf k}. \end{align*}\]

$(d)\;$ \[{\bf b}\times{\bf c}=\begin{vmatrix} {\bf i} & {\bf j} & {\bf k} \\ 1 & -1 & 0 \\ 0 & 0 & 5 \end{vmatrix} =-5{\bf i}-5{\bf j}\] so ${\bf a}\cdot({\bf b}\times{\bf c})=(4{\bf i}+3{\bf j}+{\bf k})\cdot(-5{\bf i}-5{\bf j})=-35.$

$(e)\;$ \[{\bf c}\times{\bf d}=\begin{vmatrix} {\bf i} & {\bf j} & {\bf k} \\ 0 & 0 & 5 \\ 2 & 1 & 7 \end{vmatrix} =-5{\bf i}+10{\bf j}\] so ${\bf b}\cdot({\bf c}\times{\bf d})=({\bf i}-{\bf j})\cdot(-5{\bf i}+10{\bf j})=-15.$

$(f)\;$ \[{\bf a}\times{\bf c}=\begin{vmatrix} {\bf i} & {\bf j} & {\bf k} \\ 4 & 3 & 1 \\ 0 & 0 & 5 \end{vmatrix} =15{\bf i}-20{\bf j}\] so ${\bf b}\cdot({\bf a}\times{\bf c})=({\bf i}-{\bf j})\cdot(15{\bf i}-20{\bf j})=35.$

You could also use ${\bf b}\cdot({\bf a}\times{\bf c})=-{\bf a}\cdot({\bf b}\times{\bf c})=35$ from part $(d)$.

Question 3.29 $\;$ A plane contains the three points $(1,1,1)$, $(3,3,2)$ and $(3,-1,-2)$. Find

$\;\;(a)\;\;$ a unit vector normal to the plane,

$\;\;(b)\;\;$ the Cartesian equation of the plane,

$\;\;(c)\;\;$ the shortest distance to the plane from the origin.

Quick Check

$(a)\;$ $\begin{pmatrix} -1/3 \\ 2/3 \\ -2/3 \end{pmatrix}$ (or negative of this), $\hspace{1cm}$ $(b)\;$ $x-2y+2z=1,$ $\hspace{1cm}$ $(c)\;$ $1/3.$

Solution

$(a)\;$ The points $A=(1,1,1)$, $B=(3,3,2)$ and $C=(3,-1,-2)$ have position vectors \[{\bf a}=\begin{pmatrix} 1 \\ 1 \\ 1 \end{pmatrix},\qquad {\bf b}=\begin{pmatrix} 3 \\ 3 \\ 2 \end{pmatrix},\qquad {\bf c}=\begin{pmatrix} 3 \\ -1 \\ -2 \end{pmatrix}\] and two vectors in the plane are \[{\bf u}=\overrightarrow{AB}={\bf b}-{\bf a}=\begin{pmatrix} 2 \\ 2 \\ 1 \end{pmatrix}, \qquad {\bf v}=\overrightarrow{AC}={\bf c}-{\bf a}=\begin{pmatrix} 2 \\ -2 \\ -3 \end{pmatrix}.\] Hence a normal to the plane is \[{\bf n}={\bf u}\times{\bf v}= \begin{pmatrix} 2 \\ 2 \\ 1 \end{pmatrix}\times\begin{pmatrix} 2 \\ -2 \\ -3 \end{pmatrix} =\begin{pmatrix} -4 \\ 8 \\ -8 \end{pmatrix},\] and so unit normal is \[\hat{{\bf n}}=\frac{{\bf n}}{|{\bf n}|}=\frac{1}{12}\begin{pmatrix} -4 \\ 8 \\ -8 \end{pmatrix} =\begin{pmatrix} -1/3 \\ 2/3 \\ -2/3 \end{pmatrix}.\]

$(b)\;$ Pick an arbitrary point on the plane, e.g. ${\bf a}=\begin{pmatrix} 1 \\ 1 \\ 1 \end{pmatrix}$. Then the equation of the plane is \[({\bf x}-{\bf a})\cdot{\bf n}=0 \quad\iff\quad \begin{pmatrix} x-1 \\ y-1 \\ z-1 \end{pmatrix}\cdot \begin{pmatrix} -4 \\ 8 \\ -8 \end{pmatrix}=0 \quad\iff\quad x-2y+2z=1.\] (Check the three points $A$, $B$, $C$ do satisfy this equation!)

$(c)\;$ From lectures, the distance between the origin and the plane is \[|{\bf a}\cdot\hat{{\bf n}}| = \left|\begin{pmatrix} 1 \\ 1 \\ 1 \end{pmatrix}\cdot \begin{pmatrix} -1/3 \\ 2/3 \\ -2/3 \end{pmatrix}\right|=\frac{1}{3}.\]

Question 3.30 $\;$ Using the vector product, find the vector equations of the lines

$\;\;(a)\;\;$ through the point $(1,2,3)$ and parallel to $(5,6,2)$,

$\;\;(b)\;\;$ through the point $(1,0,1)$ and parallel to $(4,3,5)$,

$\;\;(c)\;\;$ through the points $(1,1,1)$and $(2,5,3)$,

$\;\;(d)\;\;$ through the points $(0,0,0)$ and $(2,1,2)$,

$\;\;(e)\;\;$ through the point $(2,3,2)$ and perpendicular to the position vectors of $(1,1,0)$ and $(0,1,1)$,

$\;\;(f)\;\;$ through the point $(1,2,3)$ and perpendicular to the position vectors of $(2,1,1)$ and $(-1,-2,3)$.

Quick Check

$(a)\;$ $\begin{pmatrix} 2y-6z+14 \\ -2x+5z-13 \\ 6x-5y+4 \end{pmatrix}= \begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix}.$ $\hspace{2cm}$ $(b)\;$ $\begin{pmatrix} 5y-3z+3 \\ -5x+4z+1 \\3x-4y-3 \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix}.$

$(c)\;$ $\begin{pmatrix} 2y-4z+2 \\ -2x+z+1 \\ 4x-y-3 \end{pmatrix}= \begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix}.$ $\hspace{2cm}$ $(d)\;$ $\begin{pmatrix} 2y-z \\ -2x+2z \\ x-2y \end{pmatrix}= \begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix}.$

$(e)\;$ $\begin{pmatrix} y+z-5 \\ -x+z \\ -x-y+5 \end{pmatrix}= \begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix}.$ $\hspace{2cm}$ $(f)\;$ $\begin{pmatrix} -3y+7z-15 \\ 3x+5z-18 \\ -7x-5y+17 \end{pmatrix}= \begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix}.$

Solution

$(a)\;$ The vector equation of the line is $({\bf x}-{\bf a})\times{\bf d}=\boldsymbol{0}$, where ${\bf a}=\begin{pmatrix} 1\\2\\3 \end{pmatrix}$ and ${\bf d}=\begin{pmatrix} 5\\6\\2 \end{pmatrix}$.

This can be re-written as \[ \begin{pmatrix} x-1 \\ y-2 \\ z-3 \end{pmatrix}\times \begin{pmatrix} 5 \\ 6 \\ 2 \end{pmatrix}= \begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix} \quad\iff\quad \begin{pmatrix} 2y-6z+14 \\ -2x+5z-13 \\ 6x-5y+4 \end{pmatrix}= \begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix}. \]

$(b)\;$ This time, $({\bf x}-{\bf a})\times{\bf d}=\boldsymbol{0}$ where ${\bf a}=\begin{pmatrix} 1 \\ 0 \\ 1 \end{pmatrix}$ and ${\bf d}=\begin{pmatrix} 4 \\ 3 \\ 5 \end{pmatrix}$. \[ \begin{pmatrix} x-1 \\ y \\ z-1 \end{pmatrix}\times \begin{pmatrix} 4 \\ 3 \\ 5 \end{pmatrix}= \begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix} \quad\iff\quad \begin{pmatrix} 5y-3z+3 \\ -5x+4z+1 \\3x-4y-3 \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix}. \]

$(c)\;$ Here, the direction is \[{\bf d}=\begin{pmatrix} 2 \\ 5 \\ 3 \end{pmatrix} - \begin{pmatrix} 1 \\ 1 \\ 1 \end{pmatrix} = \begin{pmatrix} 1 \\ 4 \\ 2 \end{pmatrix},\] so taking ${\bf a}=\begin{pmatrix} 1 \\ 1 \\ 1 \end{pmatrix}$ gives \[ \begin{pmatrix} x-1 \\ y-1 \\ z-1 \end{pmatrix}\times \begin{pmatrix} 1 \\ 4 \\ 2 \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix} \quad\iff\quad \begin{pmatrix} 2y-4z+2 \\ -2x+z+1 \\ 4x-y-3 \end{pmatrix}= \begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix}. \]

$(d)\;$ Here ${\bf d}=\begin{pmatrix} 2 \\ 1 \\ 2\end{pmatrix} - \begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix} = \begin{pmatrix} 2 \\ 1 \\ 2 \end{pmatrix}$, so taking ${\bf a}=\begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix}$ gives \[ \begin{pmatrix} x \\ y \\ z \end{pmatrix}\times \begin{pmatrix} 2 \\ 1 \\ 2 \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix} \quad\iff\quad \begin{pmatrix} 2y-z \\ -2x+2z \\ x-2y \end{pmatrix}= \begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix}. \]

$(e)\;$ A direction perpendicular to both $\begin{pmatrix} 1 \\ 1 \\ 0 \end{pmatrix}$ and $\begin{pmatrix} 0 \\ 1 \\ 1 \end{pmatrix}$ is \[{\bf d}=\begin{pmatrix} 1 \\ 1 \\ 0 \end{pmatrix}\times \begin{pmatrix} 0 \\ 1 \\ 1 \end{pmatrix} = \begin{pmatrix} 1 \\ -1 \\ 1 \end{pmatrix}. \] Then \[ \begin{pmatrix} x-2 \\ y-3 \\ z-2 \end{pmatrix}\times \begin{pmatrix} 1 \\ -1 \\ 1 \end{pmatrix}= \begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix} \quad\iff\quad \begin{pmatrix} y+z-5 \\ -x+z \\ -x-y+5 \end{pmatrix}= \begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix}. \]

$(f)\;$ A direction perpendicular to both $\begin{pmatrix} 2 \\ 1 \\ 1 \end{pmatrix}$ and $\begin{pmatrix} -1 \\ -2 \\ 3 \end{pmatrix}$ is \[{\bf d}=\begin{pmatrix} 2 \\ 1 \\ 1 \end{pmatrix}\times \begin{pmatrix} -1 \\ -2 \\ 3 \end{pmatrix} = \begin{pmatrix} 5 \\ -7 \\ -3 \end{pmatrix}.\] Then \[ \begin{pmatrix} x-1 \\ y-2 \\ z-3 \end{pmatrix} \times\begin{pmatrix} 5 \\ -7 \\ -3 \end{pmatrix}= \begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix} \quad\iff\quad \begin{pmatrix} -3y+7z-15 \\ 3x+5z-18 \\ -7x-5y+17 \end{pmatrix}= \begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix}. \]

Question 3.31 $\;$ Find the shortest distance between the two lines \[{\bf x}=\begin{pmatrix} 2 \\ -1 \\ 1 \end{pmatrix}+t\begin{pmatrix} 1 \\ 3 \\ -2 \end{pmatrix} \qquad\text{and}\qquad {\bf x}=\begin{pmatrix} -1 \\ 3 \\ -3 \end{pmatrix}+t\begin{pmatrix} 4 \\ -1 \\ 2 \end{pmatrix}.\]

Quick Check

The distance is zero - the lines intersect!

Solution

These two lines are not parallel (the direction vectors are not multiples of each other).

The distance between lines ${\bf x}={\bf a}+t{\bf u}$ and ${\bf x}={\bf b}+t{\bf v}$ is $d=\left|({\bf a}-{\bf b})\cdot\dfrac{({\bf u}\times{\bf v})}{|{\bf u}\times{\bf v}|}\right|$.

In this case, \[{\bf u}\times{\bf v}= \begin{pmatrix} 1 \\ 3 \\ -2 \end{pmatrix}\times\begin{pmatrix} 4 \\ -1 \\ 2 \end{pmatrix} =\begin{pmatrix} 4 \\ -10 \\ -13 \end{pmatrix}\qquad\text{and}\qquad |{\bf u}\times{\bf v}|=\sqrt{285},\] so \[d=\left|\begin{pmatrix} 3 \\ -4 \\ 4 \end{pmatrix}\cdot \frac{1}{\sqrt{285}}\begin{pmatrix} 4 \\ -10 \\ -13 \end{pmatrix}\right|=0\] The lines intersect! Can you find the point of intersection?

Question 3.32 $\;$ Find the shortest distance between the two lines \[{\bf x}=\begin{pmatrix} 2 \\ -1 \\ 1 \end{pmatrix}+t\begin{pmatrix} 1 \\ 3 \\ -2 \end{pmatrix} \qquad\text{and}\qquad {\bf x}=\begin{pmatrix} -1 \\ 2 \\ -3 \end{pmatrix}+t\begin{pmatrix} 2 \\ 6 \\ -4 \end{pmatrix}.\]

Quick Check

The distance is $2\sqrt5.$

Solution

These lines are parallel because their directions are both multiples of ${\bf u}=\begin{pmatrix} 1 \\ 3 \\ -2 \end{pmatrix}$.

The distance between lines ${\bf x}={\bf a}+t{\bf u}$ and ${\bf x}={\bf b}+t{\bf u}$ is $d=\left|({\bf a}-{\bf b})\times\dfrac{{\bf u}}{|{\bf u}|}\right|$.

In this case, \[d=\left|\begin{pmatrix} 3 \\ -3 \\ 4 \end{pmatrix}\times \frac{1}{\sqrt{14}}\begin{pmatrix} 1 \\ 3 \\ -2 \end{pmatrix}\right|= \frac{1}{\sqrt{14}}\left|\begin{pmatrix} -6 \\ 10 \\ 12 \end{pmatrix}\right|=2\sqrt5.\]

Question 3.33 $\;$ By considering the distance between the two straight lines ${\bf x}={\bf a}+t{\bf u}$ and ${\bf x}={\bf b}+t{\bf v}$ where ${\bf u}\times{\bf v}\neq\boldsymbol{0}$, show that the two lines intersect if \[{\bf v}\cdot({\bf a}\times{\bf u})={\bf v}\cdot({\bf b}\times{\bf u}).\]

Quick Check

The lines are not parallel and we have a formula for the distance between them in this case. What does this imply?

Solution

The lines are not parallel since ${\bf u}\times{\bf v}\neq\boldsymbol{0}$ implies ${\bf u}$ and ${\bf v}$ are not parallel. In particular, the distance between them is given by \[d=\left|({\bf a}-{\bf b})\cdot\dfrac{({\bf u}\times{\bf v})}{|{\bf u}\times{\bf v}|}\right|. \] This vanishes, i.e. the lines intersect when $({\bf a}-{\bf b})\cdot({\bf u}\times{\bf v})=0$ and hence when \[{\bf a}\cdot({\bf u}\times{\bf v})={\bf b}\cdot({\bf u}\times{\bf v}).\] The result now follows from the cyclic property of the scalar triple product.

Question 3.34 $\;$ Suppose we are given three vectors ${\bf a}$, ${\bf b}$, ${\bf c}$ in $\mathbb{R}^3$. Explain why they are all contained in a plane precisely when ${\bf a}\cdot({\bf b}\times{\bf c})=0$.

Quick Check

Hint: think about the volume of an appropriate parallelepiped.

Solution

Recall that ${\bf a}\cdot({\bf b}\times{\bf c})$ is the volume of the parallelepiped with sides ${\bf a}$, ${\bf b}$ and ${\bf c}$. This parallelepiped has zero volume precisely when ${\bf a}$, ${\bf b}$ and ${\bf c}$ are all contained in a plane.

Question 3.35 $\;$ Differentiate the following expressions with respect to $t$, where ${\bf r}$ is a vector valued function of $t$ and ${\bf a}$, ${\bf b}$ are constant vectors.

$\;\;(a)\;\;{\bf r}\cdot{\bf r},\hspace{1cm}$ $\;\;(b)\;\;({\bf a}\cdot{\bf r}){\bf b},\hspace{1cm}$ $\;\;(c)\;\;|{\bf r}|^2{\bf r},\hspace{2cm}$ $\;\;(d)\;\;{\bf a}\times\dfrac{d{\bf r}}{dt},$

$\;\;(e)\;\;\dfrac{{\bf r}}{|{\bf r}|},\hspace{1.15cm}$ $\;\;(f)\;\;\dfrac{d{\bf r}}{dt}\cdot\dfrac{d{\bf r}}{dt},\hspace{1cm}$ $\;\;(g)\;\;{\bf r}\cdot\left(\dfrac{d{\bf r}}{dt}\times\dfrac{d^2{\bf r}}{dt^2}\right).$

Express your solutions in terms of $\dot{\bf r}$ and/or $\ddot{\bf r}$, as appropriate.

Quick Check

$(a)\;$ $2{\bf r}\cdot\dot{{\bf r}},$ $\hspace{1cm}$ $(b)\;$ $\left({\bf a}\cdot\dot{{\bf r}}\right){\bf b},$ $\hspace{1cm}$ $(c)\;$ $|{\bf r}|^2\dot{{\bf r}}+2({\bf r}\cdot\dot{{\bf r}}){\bf r},$ $\hspace{1cm}$ $(d)\;$ ${\bf a}\times\ddot{{\bf r}},$

$(e)\;$ $\dfrac{1}{|{\bf r}|}\dot{{\bf r}}-\dfrac{1}{|{\bf r}|^3}({\bf r}\cdot\dot{{\bf r}}){\bf r},$ $\hspace{1cm}$ $(f)\;$ $2\dot{{\bf r}}\cdot\ddot{{\bf r}},$ $\hspace{1cm}$ $(g)\;$ ${\bf r}\cdot\left(\dot{{\bf r}}\times\dddot{{\bf r}}\right).$

Solution

$(a)\;$ Use the product rule, \[\frac{d}{dt}({\bf r}\cdot{\bf r}) ={\bf r}\cdot\dot{{\bf r}}+\dot{{\bf r}}\cdot{\bf r}=2{\bf r}\cdot\dot{{\bf r}}.\]

$(b)\;$ Use the product rule and $\dfrac{d\,{\bf b}}{dt}=\boldsymbol{0}$, \[\frac{d}{dt}\left(({\bf a}\cdot{\bf r}){\bf b}\right) =({\bf a}\cdot{\bf r})\frac{d\,{\bf b}}{dt}+\left(\frac{d}{dt}({\bf a}\cdot{\bf r})\right){\bf b} =\left({\bf a}\cdot\dot{{\bf r}}\right){\bf b}.\]

$(c)\;$ Use $|{\bf r}|^2={\bf r}\cdot{\bf r}$, the product rule and part (a), \[\begin{align*} \frac{d}{dt}\left(|{\bf r}|^2{\bf r}\right) =\frac{d}{dt}\left(({\bf r}\cdot{\bf r}){\bf r}\right) &=({\bf r}\cdot{\bf r})\frac{d{\bf r}}{dt}+\left(\frac{d}{dt}({\bf r}\cdot{\bf r})\right){\bf r} \\ &=|{\bf r}|^2\dot{{\bf r}}+2({\bf r}\cdot\dot{{\bf r}}){\bf r}. \end{align*}\]

$(d)\;$ Use the product rule and $\dfrac{d{\bf a}}{dt}=\boldsymbol{0}$, \[\begin{align*} \frac{d}{dt}\left({\bf a}\times\dot{{\bf r}}\right) &={\bf a}\times\ddot{{\bf r}}+\frac{d{\bf a}}{dt}\times\dot{{\bf r}} ={\bf a}\times\ddot{{\bf r}}. \end{align*}\]

$(e)\;$ Use the chain rule and product rule to differentiate both sides of the identity $|{\bf r}|^2={\bf r}\cdot{\bf r}$, \[2|{\bf r}|\frac{d}{dt}|{\bf r}|=2{\bf r}\cdot\dot{{\bf r}}\qquad\implies\qquad \frac{d}{dt}|{\bf r}|=\frac{{\bf r}\cdot\dot{{\bf r}}}{|{\bf r}|}\] Then \[\begin{align*} \frac{d}{dt}\,\frac{{\bf r}}{|{\bf r}|} &=\frac{1}{|{\bf r}|}\dot{{\bf r}}+\left(\frac{d}{dt}\frac{1}{|{\bf r}|}\right){\bf r} \\ &=\frac{1}{|{\bf r}|}\dot{{\bf r}}-\left(\frac{1}{|{\bf r}|^2}\frac{d}{dt}|{\bf r}|\right){\bf r} \\ &=\frac{1}{|{\bf r}|}\dot{{\bf r}}-\frac{1}{|{\bf r}|^3}({\bf r}\cdot\dot{{\bf r}}){\bf r}. \end{align*}\]

$(f)\;$ Use the product rule, \[\frac{d}{dt}\left(\dot{{\bf r}}\cdot{{\dot{\bf r}}}\right)=2\dot{{\bf r}}\cdot\ddot{{\bf r}}.\]

$(g)\;$ Use product rules and the facts ${\bf u}\times{\bf u}=\bf0$ and ${\bf u}\cdot({\bf u}\times{\bf v})=0$, \[\begin{align*} \frac{d}{dt}\left({\bf r}\cdot\left(\dot{{\bf r}}\times\ddot{{\bf r}}\right)\right) &={\bf r}\cdot\frac{d}{dt}\left(\dot{{\bf r}}\times\ddot{{\bf r}}\right) +\left(\frac{d}{dt}{\bf r}\right)\cdot\left(\dot{{\bf r}}\times\ddot{{\bf r}}\right) \\ &={\bf r}\cdot\left(\dot{{\bf r}}\times\dddot{{\bf r}}+\ddot{{\bf r}}\times\ddot{{\bf r}}\right) +\dot{{\bf r}}\cdot(\dot{{\bf r}}\times\ddot{{\bf r}}) \\ &={\bf r}\cdot\left(\dot{{\bf r}}\times\dddot{{\bf r}}\right). \end{align*}\]

Question 3.36 $\;$ The position of an ant in the $xy$-plane as a function of time $t$ is \[{\bf r}(t)={\bf i}\cos(\omega t)+{\bf j}\sin(\omega t).\]

$\;\;(a)\;\;$ Show that the ant moves in a circle.

$\;\;(b)\;\;$ Calculate $\dfrac{d{\bf r}}{dt}$, $\dfrac{d^2{\bf r}}{dt^2}$ and $\dfrac{d{\bf r}}{dt}\cdot\dfrac{d^2{\bf r}}{dt^2}$.

$\;\;(c)\;\;$ If the ant has mass $m$, calculate its angular momentum $\displaystyle{\bf L}={\bf r}\times m\frac{d{\bf r}}{dt}$.

Quick Check

$(a)\;$ How are the $x$ and $y$ coordinates related at time $t$?

$(b)\;$ $\dfrac{d{\bf r}}{dt}=-{\bf i}\,\omega\sin(\omega t)+{\bf j}\,\omega\cos(\omega t)$, $\;\dfrac{d^2{\bf r}}{dt^2}=-\omega^2{\bf r}$ and $\;\dfrac{d{\bf r}}{dt}\cdot\dfrac{d^2{\bf r}}{dt^2}=0$.

$(c)\;$ ${\bf L}=m\omega{\bf k}.$

Solution

$(a)\;$ At any time, $x^2+y^2=\cos^2(\omega t)+\sin^2(\omega t)=1$ (and $z=0$) which is a circle.

$(b)\;$ We have \[\begin{align*} \dfrac{d{\bf r}}{dt} &=-{\bf i}\,\omega\sin(\omega t)+{\bf j}\,\omega\cos(\omega t), \\ \dfrac{d^2{\bf r}}{dt^2} &=-{\bf i}\,\omega^2\cos(\omega t)-{\bf j}\,\omega^2\sin(\omega t)=-\omega^2{\bf r}, \\ \text{and}\quad\dfrac{d{\bf r}}{dt}\cdot\dfrac{d^2{\bf r}}{dt^2} &=\omega^3\sin(\omega t)\cos(\omega t)-\omega^3\cos(\omega t)\sin(\omega t)=0. \end{align*}\] (so at any time, the velocity and acceleration are perpendicular to each other).

$(c)\;$ We have \[{\bf L}= \begin{pmatrix} \cos(\omega t) \\ \sin(\omega t) \\ 0 \end{pmatrix}\times \begin{pmatrix} -m\omega\sin(\omega t) \\ m\omega\cos(\omega t) \\ 0 \end{pmatrix} =\begin{pmatrix} 0 \\ 0 \\ m\omega \end{pmatrix}=m\omega{\bf k},\] Notice this angular momentum doesn’t change with respect to time.

Question 3.37 $\;$ The position of a fly in $\mathbb{R}^3$ as a function of time $t$ is \[{\bf r}(t)=\begin{pmatrix} R\cos(\omega t) \\ R\sin(\omega t) \\ t \end{pmatrix},\] for constants $R$ and $\omega$. Describe the flightpath of the fly and find its velocity and acceleration at time $t$.

Quick Check

The flightpath is a helix (i.e. a corkscrew shape), and \[\dot{{\bf r}}(t)=\begin{pmatrix} -R\omega\sin(\omega t) \\ R\omega\cos(\omega t) \\ 1 \end{pmatrix},\qquad \ddot{{\bf r}}(t)=-R\omega^2\begin{pmatrix} \cos(\omega t) \\ \sin(\omega t) \\ 0 \end{pmatrix}.\]

Solution

The coordinates satisfy $x^2+y^2=R^2$ and $z=t$. That means the fly is rotating in a circular way around the $z$-axis whilst moving upwards at constant speed, i.e. the flightpath is a helix.

The velocity and acceleration are: \[\dot{{\bf r}}(t)=\begin{pmatrix} -R\omega\sin(\omega t) \\ R\omega\cos(\omega t) \\ 1 \end{pmatrix} \] and \[ \ddot{{\bf r}}(t)=\begin{pmatrix} -R\omega^2\cos(\omega t) \\ -R\omega^2\sin(\omega t) \\ 0 \end{pmatrix} =-R\omega^2\begin{pmatrix} \cos(\omega t) \\ \sin(\omega t) \\ 0 \end{pmatrix}. \] (In particular, the acceleration is always directly towards the $z$-axis.)

Question 3.38 $\;$ An electron with position vector ${\bf r}$, charge $e$ and mass $m$ moves in a constant magnetic field ${\bf B}$ according to the equation \[m\frac{d^2{\bf r}}{dt^2}=e\frac{d{\bf r}}{dt}\times {\bf B}.\] Show that the kinetic energy $E=\dfrac{m}{2}\left|\dfrac{d{\bf r}}{dt}\right|^2$ is constant in time. Hint: show that $\dfrac{dE}{dt}=0$.

Quick Check

Hint: differentiate with the product rule and remember when scalar products vanish.

Solution

Differentiating $E=\frac12m\dot{{\bf r}}\cdot\dot{{\bf r}}$ gives \[\begin{align*} \frac{dE}{dt}=\frac12m\dot{{\bf r}}\cdot\ddot{{\bf r}}+\frac12m\ddot{{\bf r}}\cdot\dot{{\bf r}} =m\dot{{\bf r}}\cdot\ddot{{\bf r}}=\dot{{\bf r}}\cdot\left(e\dot{{\bf r}}\times{\bf B}\right). \end{align*}\] This is zero since $\dot{{\bf r}}$ and $\dot{{\bf r}}\times{\bf B}$ are perpendicular and so $E$ is constant.

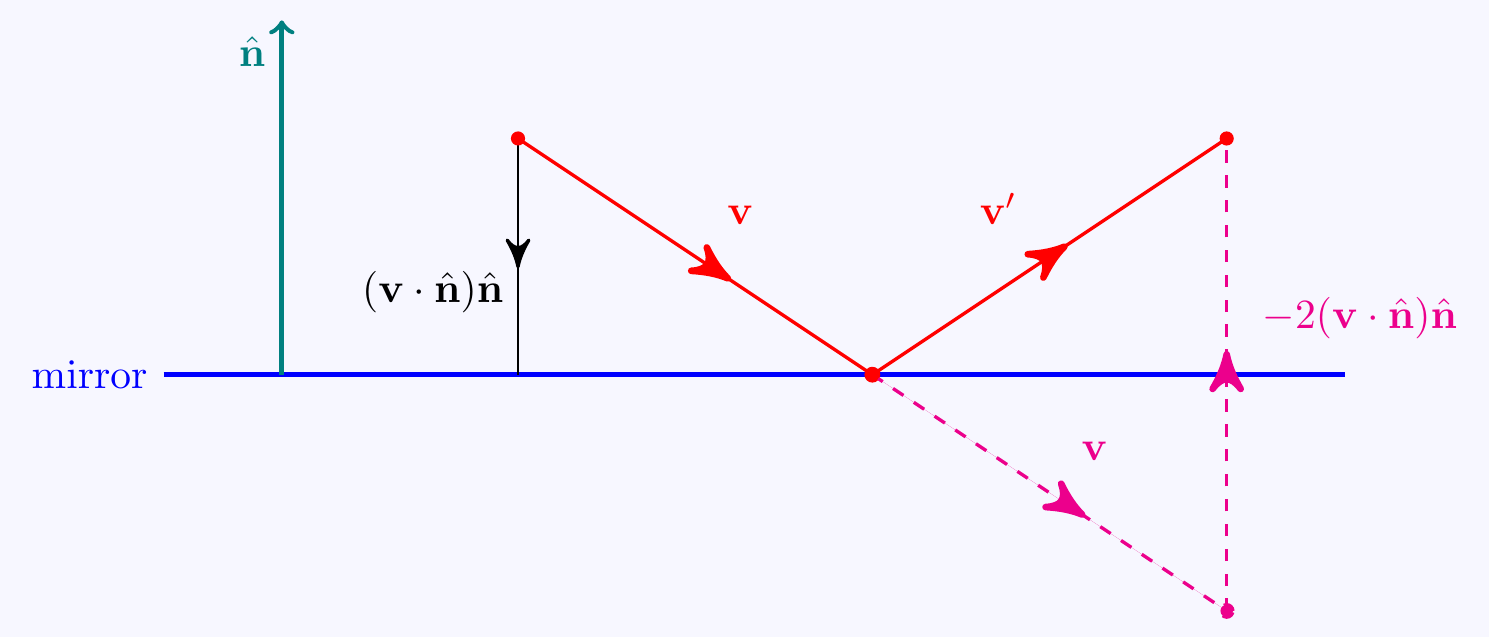
Question 3.39 $\;$ A ray of light travelling in the direction of the vector ${\bf v}$ is reflected in a mirror which has unit normal $\hat{{\bf n}}$. Find the direction vector of the reflected ray. (Draw a picture!)

Quick Check

The reflected ray has direction ${\bf v}'={\bf v}-2({\bf v}\cdot\hat{{\bf n}})\hat{{\bf n}}.$

Solution

The reflected ray has direction \[{\bf v}'={\bf v}-2({\bf v}\cdot\hat{{\bf n}})\hat{{\bf n}}.\] To see this, look at the diagram and use the fact that the projection of ${\bf v}$ onto $\hat{{\bf n}}$ is $({\bf v}\cdot\hat{{\bf n}})\hat{{\bf n}}$.

Week 10 Material

Question 3.40 $\;$ Find the characteristic polynomials and eigenvalues of the following matrices:

$\;\;(a)\;\;\begin{pmatrix} 1 & 0 \\ 7 & 3 \end{pmatrix},\hspace{1.65cm}$ $\;\;(b)\;\;\begin{pmatrix} 1 & 2 \\ 1 & -1 \end{pmatrix},\hspace{2cm}$ $\;\;(c)\;\;\begin{pmatrix} 2 & -4 \\ 4 & -6 \end{pmatrix},$

$\;\;(d)\;\;\begin{pmatrix} 3 & -1 \\ -6 & 2 \end{pmatrix},\hspace{1cm}$ $\;\;(e)\;\;\begin{pmatrix} 1 & -1 & 0 \\ 1 & 3 & -2 \\ 1 & 1 & -1 \end{pmatrix},\hspace{1cm}$ $\;\;(f)\;\;\begin{pmatrix} 0 & 1 & 1 \\ 1 & 0 & 1 \\ 1 & 1 & 0 \end{pmatrix},$

$\;\;(g)\;\;\begin{pmatrix} 0 & 1 & 2 \\ 1 & 0 & 1 \\ 2 & 1 & 0 \end{pmatrix},\hspace{1cm}$ $\;\;(h)\;\;\begin{pmatrix} 3 & 4 & 2 \\ -1 & 1 & 2 \\ 1 & -2 & -1 \end{pmatrix}.$

Quick Check

$(a)\;$ The eigenvalues are $\lambda=1,3$. $(b)\;$ The eigenvalues are $\lambda=\pm\sqrt{3}$.

$(c)\;$ The eigenvalues are $\lambda=-2,-2$.

$(d)\;$ The eigenvalues are $\lambda=0, 5$.

$(e)\;$ The eigenvalues are $\lambda=0, 1, 2$.

$(f)\;$ The eigenvalues are $\lambda=2, -1, -1$.

$(g)\;$ The eigenvalues are $\lambda=-2, 1+\sqrt{3}, 1-\sqrt{3}$.

$(h)\;$ The eigenvalues are $\lambda=3, +i\sqrt{5}, -i\sqrt{5}$.

Solution

$(a)\;$ The characteristic polynomial is \[\det(A-\lambda I)= \begin{vmatrix} 1-\lambda & 0 \\ 7 & 3-\lambda \end{vmatrix} =(1-\lambda)(3-\lambda)\] and so the eigenvalues are $\lambda=1,3$.

(It’s easy to find eigenvalues of triangular matrices! They are just the diagonal entries.)

$(b)\;$ The characteristic polynomial is \[\begin{align*} \det(A-\lambda I) &= \begin{vmatrix} 1-\lambda & 2 \\ 1 & -1-\lambda \end{vmatrix} \\ &=(1-\lambda)(-1-\lambda)-2=\lambda^2-3 \end{align*}\] and so the eigenvalues are $\lambda=\pm\sqrt{3}$.

$(c)\;$ The characteristic polynomial is \[\begin{align*} \det(A-\lambda I) &= \begin{vmatrix} 2-\lambda & -4 \\ 4 & -6-\lambda \end{vmatrix} =(2-\lambda)(-6-\lambda)+16 \\ &= \lambda^2+4\lambda+4=(\lambda+2)^2 \end{align*}\] and so the eigenvalues are $\lambda=-2,-2$.

$(d)\;$ The characteristic polynomial is \[\begin{align*} \det(A-\lambda I)= \begin{vmatrix} 3-\lambda & -1 \\ -6 & 2-\lambda \end{vmatrix} &=(3-\lambda)(2-\lambda)-6 \\ &=\lambda^2-5\lambda \end{align*}\] and so the eigenvalues are $\lambda=0, 5$.

$(e)\;$ The characteristic polynomial $\det(A-\lambda I)$ is \[\begin{align*} \begin{vmatrix} 1-\lambda & -1 & 0 \\ 1 & 3-\lambda & -2 \\ 1 & 1 & -1-\lambda \end{vmatrix} &=(1-\lambda)\begin{vmatrix} 3-\lambda & -2 \\ 1 & -1-\lambda \end{vmatrix} +\begin{vmatrix} 1 & -2 \\ 1 & -1-\lambda \end{vmatrix} \\ &=(1-\lambda)[(3-\lambda)(-1-\lambda)+2]+(-1-\lambda+2) \\ &=(1-\lambda)(-1-2\lambda+\lambda^2)+(1-\lambda) \\ &=(1-\lambda)(\lambda^2-2\lambda)=-\lambda(\lambda-1)(\lambda-2) \end{align*}\] and so the eigenvalues are $\lambda=0, 1, 2$.

$(f)\;$ Sometimes a row operation or two can help with the factorisation:

The characteristic polynomial $\det(A-\lambda I)$ is \[\begin{align*} \begin{vmatrix} -\lambda & 1 & 1 \\ 1 & -\lambda & 1 \\ 1 & 1 & -\lambda \end{vmatrix} &\;\;\overset{R_1+\lambda R_3}{\overset{R_2-R_3}{\overset{\,}{=}}}\;\; \begin{vmatrix} 0 & 1+\lambda & 1-\lambda^2 \\ 0 & -1-\lambda & 1+\lambda \\ 1 & 1 & -\lambda \end{vmatrix} \\ &=\begin{vmatrix} 1+\lambda & 1-\lambda^2 \\ -1-\lambda & 1+\lambda \end{vmatrix} \\ &=(1+\lambda)^2+(1+\lambda)(1-\lambda^2) \\ &=(1+\lambda)(2+\lambda-\lambda^2) \\ &=-(\lambda+1)^2(\lambda-2) \end{align*}\] and so the eigenvalues are $\lambda=2, -1, -1$.

$(g)\;$ The characteristic polynomial $\det(A-\lambda I)$ is \[\begin{align*} \begin{vmatrix} -\lambda & 1 & 2 \\ 1 & -\lambda & 1 \\ 2 & 1 & -\lambda \end{vmatrix} &\;\;\overset{R_1+\lambda R_2}{\overset{R_3-2R_2}{\overset{\,}{=}}}\;\; \begin{vmatrix} 0 & 1-\lambda^2 & 2+\lambda \\ 1 & -\lambda & 1 \\ 0 & 1+2\lambda & -2-\lambda \end{vmatrix} \\ &=-\begin{vmatrix} 1-\lambda^2 & 2+\lambda \\ 1+2\lambda & -\lambda-2 \end{vmatrix} \\ &=-(2+\lambda)\begin{vmatrix} 1-\lambda^2 & 1 \\ 1+2\lambda & -1 \end{vmatrix} \\ &=-(\lambda+2)(\lambda^2-2\lambda-2) \end{align*}\] and so the eigenvalues are $\lambda=-2, 1+\sqrt{3}, 1-\sqrt{3}$.

$(h)\;$ The characteristic polynomial $\det(A-\lambda I)$ is \[\begin{align*} \begin{vmatrix} 3-\lambda & 4 & 2 \\ -1 & 1-\lambda & 2 \\ 1 & -2 & -1-\lambda \end{vmatrix} &=(3-\lambda)\begin{vmatrix} 1-\lambda & 2 \\ -2 & -1-\lambda \end{vmatrix} \\ &\hspace{1.3cm} -4\begin{vmatrix} -1 & 2 \\ 1 & -1-\lambda \end{vmatrix} +2\begin{vmatrix} -1 & 1-\lambda \\ 1 & -2 \end{vmatrix} \\[5pt] &=(3-\lambda)(\lambda^2+3)-4(\lambda-1)+2(\lambda+1) \\ &=(3-\lambda)(\lambda^2+3)+2(3-\lambda) \\ &=-(\lambda-3)(\lambda^2+5) \end{align*}\] and so the eigenvalues are $\lambda=3, +i\sqrt{5}, -i\sqrt{5}$.

Question 3.41 $\;$ Find the eigenvalues and corresponding eigenspaces of the following matrices:

$\;\;(a)\;\;\begin{pmatrix} 3 & 2 \\ 3 & -2 \end{pmatrix},\hspace{1.7cm}$ $\;\;(b)\;\;\begin{pmatrix} 6 & -4 \\ 3 & -1 \end{pmatrix},\hspace{2.3cm}$ $\;\;(c)\;\;\begin{pmatrix} 2 & -3 \\ 3 & -4 \end{pmatrix}$

$\;\;(d)\;\;\begin{pmatrix} -1 & -3 & 3 \\ -3 & -1 & 3 \\ -3 & -3 & 5 \end{pmatrix},\hspace{0.7cm}$ $\;\;(e)\;\;\begin{pmatrix} -2 & -2 & -5 \\ -7 & -3 & -11 \\ 4 & 2 & 7 \end{pmatrix},\hspace{0.7cm}$ $\;\;(f)\;\;\begin{pmatrix} 5 & 6 & -2 \\ -1 & -2 & 3 \\ -1 & -1 & 2 \end{pmatrix},$

$\;\;(g)\;\;\begin{pmatrix} 1 & 1 \\ -2 & -1 \end{pmatrix},\hspace{1.35cm}$ $\;\;(h)\;\;\begin{pmatrix} \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \end{pmatrix} \;\;\text{where $\theta$ is not a whole multiple of $\pi$.}$

Quick Check

$(a)\;$ The eigenvalues are $\lambda=-3, 4$ and the corresponding eigenspaces are \[V_{-3}=\operatorname{Span} \left\{\begin{pmatrix} 1 \\ -3 \end{pmatrix}\right\}, \qquad V_{4}=\operatorname{Span} \left\{\begin{pmatrix} 2 \\ 1 \end{pmatrix}\right\}.\]

$(b)\;$ The eigenvalues are $\lambda=2, 3$ and the corresponding eigenspaces are \[V_{2}=\operatorname{Span}\left\{\begin{pmatrix} 1 \\ 1 \end{pmatrix}\right\}, \qquad V_{3}=\operatorname{Span}\left\{\begin{pmatrix} 4 \\ 3 \end{pmatrix}\right\}.\]

$(c)\;$ The eigenvalues are $\lambda=-1, -1$, (i.e. a repeated eigenvalue) and the corresponding eigenspace is \[V_{-1}=\operatorname{Span}\left\{\begin{pmatrix} 1 \\ 1 \end{pmatrix}\right\}.\]

$(d)\;$ The eigenvalues are $\lambda=-1, 2, 2$ and the corresponding eigenspaces are \[V_{-1}=\operatorname{Span}\left\{\begin{pmatrix} 1 \\ 1 \\ 1 \end{pmatrix}\right\}, \qquad V_{2}=\operatorname{Span}\left\{\begin{pmatrix} 1 \\ 0 \\ 1 \end{pmatrix}, \begin{pmatrix} 0 \\ 1 \\ 1 \end{pmatrix}\right\}.\]

$(e)\;$ The eigenvalues are $\lambda=-1, 1, 2$ and the corresponding eigenspaces are \[V_{-1}=\operatorname{Span}\left\{\begin{pmatrix} -1 \\ -2 \\ 1 \end{pmatrix}\right\},\qquad V_{1}=\operatorname{Span}\left\{\begin{pmatrix} -1 \\ -1 \\ 1 \end{pmatrix}\right\}, \qquad V_{2}=\operatorname{Span}\left\{\begin{pmatrix} 1 \\ 3 \\ -2 \end{pmatrix}\right\}.\]

$(f)\;$ The eigenvalues are $\lambda=-1, 3, 3$ and the corresponding eigenspaces are \[V_{-1}=\operatorname{Span}\left\{\begin{pmatrix} 1 \\ -1 \\ 0 \end{pmatrix}\right\}, \qquad V_{3}=\operatorname{Span}\left\{\begin{pmatrix} -2 \\ 1 \\ 1 \end{pmatrix}\right\}.\]

$(g)\;$ The eigenvalues are $\lambda=\pm i$ and the corresponding eigenspaces are \[V_{i}=\operatorname{Span}\left\{\begin{pmatrix} -1 \\ 1-i \end{pmatrix}\right\}, \qquad V_{-i}=\operatorname{Span}\left\{\begin{pmatrix} -1 \\ 1+i \end{pmatrix}\right\}.\]

$(h)\;$ The eigenvalues are $\lambda=e^{\pm i\theta}$ and the corresponding eigenspaces are \[V_{e^{i\theta}}=\operatorname{Span}\left\{\begin{pmatrix} i \\ 1 \end{pmatrix}\right\},\qquad V_{e^{-i\theta}}=\operatorname{Span}\left\{\begin{pmatrix} 1 \\ i \end{pmatrix}\right\}.\]

Solutions

$(a)\;$ First find eigenvalues: \[\begin{align*} \det(A-\lambda I) &=\begin{vmatrix} 3-\lambda & 2 \\ 3 & -2-\lambda \end{vmatrix} =(3-\lambda)(-2-\lambda)-6 \\ &=\lambda^2-\lambda-12=(\lambda+3)(\lambda-4) \end{align*}\] so the eigenvalues are $\lambda=-3, 4$.

For $\lambda=-3$, the eigenvectors ${\bf v}=\begin{pmatrix} x \\ y \end{pmatrix}$ satisfy $(A+3I){\bf v}={\bf 0}$: \[\left(\begin{array}{cc|c} 6 & 2 & 0 \\ 3 & 1 & 0 \end{array}\right) \xrightarrow{R_1-2R_2} \left(\begin{array}{cc|c} 0 & 0 & 0 \\ 3 & 1 & 0\end{array}\right)\] So $3x+y=0$ and the corresponding eigenspace is $V_{-3}=\operatorname{Span} \left\{\begin{pmatrix} 1 \\ -3 \end{pmatrix}\right\}$.

For $\lambda=4$, the eigenvectors ${\bf v}=\begin{pmatrix} x \\ y \end{pmatrix}$ satisfy $(A-4I){\bf v}={\bf 0}$: \[\left(\begin{array}{cc|c} -1 & 2 & 0 \\ 3 & -6 & 0 \end{array}\right) \xrightarrow{R_2+3R_1} \left(\begin{array}{cc|c} -1 & 2 & 0 \\ 0 & 0 & 0 \end{array}\right)\] So $-x+2y=0$ and the corresponding eigenspace is $V_{4}=\operatorname{Span} \left\{\begin{pmatrix} 2 \\ 1 \end{pmatrix}\right\}$.

$(b)\;$ First find eigenvalues: \[\begin{align*} \det(A-\lambda I) &=\begin{vmatrix} 6-\lambda & -4 \\ 3 & -1-\lambda \end{vmatrix} =(6-\lambda)(-1-\lambda)+12 \\ &=\lambda^2-5\lambda+6=(\lambda-2)(\lambda-3) \end{align*}\] so the eigenvalues are $\lambda=2, 3$.

For $\lambda=2$, the eigenvectors ${\bf v}=\begin{pmatrix} x \\ y \end{pmatrix}$ satisfy $(A-2I){\bf v}={\bf 0}$: \[\left(\begin{array}{cc|c} 4 & -4 & 0 \\ 3 & -3 & 0 \end{array}\right) \xrightarrow{(1/4)R_1} \left(\begin{array}{cc|c} 1 & -1 & 0 \\ 3 & -3 & 0\end{array}\right) \xrightarrow{R_2-3R_1} \left(\begin{array}{cc|c} 1 & -1 & 0 \\ 0 & 0 & 0\end{array}\right)\] So $x-y=0$ and the corresponding eigenspace is $V_{2}=\operatorname{Span}\left\{\begin{pmatrix} 1 \\ 1 \end{pmatrix}\right\}$.

For $\lambda=3$, the eigenvectors ${\bf v}=\begin{pmatrix} x \\ y \end{pmatrix}$ satisfy $(A-3I){\bf v}={\bf 0}$: \[\left(\begin{array}{cc|c} 3 & -4 & 0 \\ 3 & -4 & 0 \end{array}\right) \xrightarrow{R_2-R_1} \left(\begin{array}{cc|c} 3 & -4 & 0 \\ 0 & 0 & 0 \end{array}\right)\] So $3x-4y=0$ and the corresponding eigenspace is $V_{3}=\operatorname{Span}\left\{\begin{pmatrix} 4 \\ 3 \end{pmatrix}\right\}$.

$(c)\;$ First find eigenvalues: \[\begin{align*} \det(A-\lambda I) &=\begin{vmatrix} 2-\lambda & -3 \\ 3 & -4-\lambda \end{vmatrix} =(2-\lambda)(-4-\lambda)+9 \\ &=\lambda^2+2\lambda+1=(\lambda+1)^2 \end{align*}\] so the eigenvalues are $\lambda=-1, -1$, (i.e. a repeated eigenvalue).

For $\lambda=-1$, the eigenvectors ${\bf v}=\begin{pmatrix} x \\ y \end{pmatrix}$ satisfy $(A+I){\bf v}={\bf 0}$: \[\left(\begin{array}{cc|c} 3 & -3 & 0 \\ 3 & -3 & 0 \end{array}\right) \xrightarrow{R_2-R_1} \left(\begin{array}{cc|c} 3 & -3 & 0 \\ 0 & 0 & 0\end{array}\right) \xrightarrow{(1/3)R_1} \left(\begin{array}{cc|c} 1 & -1 & 0 \\ 0 & 0 & 0\end{array}\right) \] So $x-y=0$ and the corresponding eigenspace is $V_{-1}=\operatorname{Span}\left\{\begin{pmatrix} 1 \\ 1 \end{pmatrix}\right\}$.

$(d)\;$ The characteristic polynomial $\det(A-\lambda I)$ is \[\begin{align*} \begin{vmatrix} -1-\lambda & -3 & 3 \\ -3 & -1-\lambda & 3 \\ -3 & -3 & 5-\lambda \end{vmatrix} & \;\;{\overset{C_3+C_2}{\overset{\,}{=}}}\;\; \begin{vmatrix} -1-\lambda & -3 & 0 \\ -3 & -1-\lambda & 2-\lambda \\ -3 & -3 & 2-\lambda \end{vmatrix} \\ & \;\;{\overset{R_2-R_3}{\overset{\,}{=}}}\;\; \begin{vmatrix} -1-\lambda & -3 & 0 \\ 0 & 2-\lambda & 0 \\ -3 & -3 & 2-\lambda \end{vmatrix} \\ &=(2-\lambda)\begin{vmatrix} -1-\lambda & 0 \\ -3 & 2-\lambda \end{vmatrix} \\ &=-(\lambda+1)(\lambda-2)^2 \end{align*}\] and so the eigenvalues are $\lambda=-1, 2, 2$.

For $\lambda=-1$, the eigenvectors ${\bf v}=\begin{pmatrix} x \\ y \\ z\end{pmatrix}$ satisfy $(A+I){\bf v}={\bf 0}$: \[ \left(\begin{array}{ccc|c} 0 & -3 & 3 & 0 \\ -3 & 0 & 3 & 0 \\ -3 & -3 & 6 & 0 \end{array}\right) \xrightarrow{R_3-R_1} \left(\begin{array}{ccc|c} 0 & -3 & 3 & 0 \\ -3 & 0 & 3 & 0 \\ -3 & 0 & 3 & 0 \end{array}\right) \xrightarrow{R_3-R_2} \left(\begin{array}{ccc|c} 0 & -3 & 3 & 0 \\ -3 & 0 & 3 & 0 \\ 0 & 0 & 0 & 0 \end{array}\right)\] \[\xrightarrow[(-1/3)R_2]{(-1/3)R_1} \left(\begin{array}{ccc|c} 0 & 1 & -1 & 0 \\ 1 & 0 & -1 & 0 \\ 0 & 0 & 0 & 0 \end{array}\right).\]

So $x=y=z$ and the corresponding eigenspace is $V_{-1}=\operatorname{Span}\left\{\begin{pmatrix} 1 \\ 1 \\ 1 \end{pmatrix}\right\}$.

For $\lambda=2$, the eigenvectors ${\bf v}=\begin{pmatrix} x \\ y \\ z\end{pmatrix}$ satisfy $(A-2I){\bf v}={\bf 0}$: \[ \left(\begin{array}{ccc|c} -3 & -3 & 3 & 0 \\ -3 & -3 & 3 & 0 \\ -3 & -3 & 3 & 0 \end{array}\right) \xrightarrow[R_2-R_1]{R_3-R_1} \left(\begin{array}{ccc|c} -3 & -3 & 3 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{array}\right) \xrightarrow{(-1/3)R_1} \left(\begin{array}{ccc|c} 1 & 1 & -1 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{array}\right) \] So $x+y-z=0$ and setting $x=\mu$, $y=\nu$ gives \[{\bf v} = \begin{pmatrix} \mu \\ \nu \\ \mu+\nu \end{pmatrix} =\mu\begin{pmatrix} 1 \\ 0 \\ 1 \end{pmatrix} +\nu\begin{pmatrix} 0 \\ 1 \\ 1 \end{pmatrix}.\] The corresponding eigenspace can be written $\;\; V_{2}=\operatorname{Span}\left\{\begin{pmatrix} 1 \\ 0 \\ 1 \end{pmatrix}, \begin{pmatrix} 0 \\ 1 \\ 1 \end{pmatrix}\right\}$.

$(e)\;$ The characteristic polynomial $\det(A-\lambda I)$ is $\;$ \[\begin{align*} \begin{vmatrix} -2-\lambda & -2 & -5 \\ -7 & -3-\lambda & -11 \\ 4 & 2 & 7-\lambda \end{vmatrix} &=(-2-\lambda)\begin{vmatrix} -3-\lambda & -11 \\ 2 & 7-\lambda \end{vmatrix} \\ &\hspace{1cm} +2\begin{vmatrix} -7 & -11 \\ 4 & 7-\lambda \end{vmatrix} -5\begin{vmatrix} -7 & -3-\lambda \\ 4 & 2 \end{vmatrix} \\[5pt] &=(-2-\lambda)(\lambda^2-4\lambda+1)+2(7\lambda-5)-5(4\lambda-2) \\ &=(-2-\lambda)(\lambda^2-4\lambda+1)-6\lambda \\ &=-\lambda^3+2\lambda^2+\lambda-2 \end{align*}\] It’s not so easy to solve a general cubic equation. But if it has “nice” integer roots, they would have to divide the constant term 2, so try $\pm 1 ,\pm 2$. In this case, we find three eigenvalues $\lambda=-1, 1, 2$.

For $\lambda=-1$, the eigenvectors ${\bf v}=\begin{pmatrix} x \\ y \\ z\end{pmatrix}$ satisfy $(A+I){\bf v}={\bf 0}$:

\[ \left(\begin{array}{ccc|c} -1 & -2 & -5 & 0 \\ -7 & -2 & -11 & 0 \\ 4 & 2 & 8 & 0 \end{array}\right) \xrightarrow[R_3+4R_1]{R_2-7R_1} \left(\begin{array}{ccc|c} -1 & -2 & -5 & 0 \\ 0 & 12 & 24 & 0 \\ 0 & -6 & -12 & 0 \end{array}\right) \xrightarrow[(-1/6)R_3]{(1/12)R_1} \left(\begin{array}{ccc|c} -1 & -2 & -5 & 0 \\ 0 & 1 & 2 & 0 \\ 0 & 1 & 2 & 0 \end{array}\right)\] \[\xrightarrow[R_3-R_2]{-R_1} \left(\begin{array}{ccc|c} 1 & 2 & 5 & 0 \\ 0 & 1 & 2 & 0 \\ 0 & 0 & 0 & 0 \end{array}\right) \xrightarrow{R_1-2R_2} \left(\begin{array}{ccc|c} 1 & 0 & 1 & 0 \\ 0 & 1 & 2 & 0 \\ 0 & 0 & 0 & 0 \end{array}\right).\] So $x=-z$ and $y=-2z$ and the corresponding eigenspace is $V_{-1}=\operatorname{Span}\left\{\begin{pmatrix} -1 \\ -2 \\ 1 \end{pmatrix}\right\}$.

For $\lambda=1$, the eigenvectors ${\bf v}=\begin{pmatrix} x \\ y \\ z\end{pmatrix}$ satisfy $(A-I){\bf v}={\bf 0}$: \[ \left(\begin{array}{ccc|c} -3 & -2 & -5 & 0 \\ -7 & -4 & -11 & 0 \\ 4 & 2 & 6 & 0 \end{array}\right) \xrightarrow[]{R_1+R_3} \left(\begin{array}{ccc|c} 1 & 0 & 1 & 0 \\ -7 & -4 & -11 & 0 \\ 4 & 2 & 6 & 0 \end{array}\right)\] \[ \xrightarrow[R_3-4R_1]{R_2+7R_1} \left(\begin{array}{ccc|c} 1 & 0 & 1 & 0 \\ 0 & -4 & -4 & 0 \\ 0 & 2 & 2 & 0 \end{array}\right) \xrightarrow{(-1/4)R_2} \left(\begin{array}{ccc|c} 1 & 0 & 1 & 0 \\ 0 & 1 & 1 & 0 \\ 0 & 2 & 2 & 0 \end{array}\right) \xrightarrow{R_3-2R_2} \left(\begin{array}{ccc|c} 1 & 0 & 1 & 0 \\ 0 & 1 & 1 & 0 \\ 0 & 0 & 0 & 0 \end{array}\right).\] So $x=-z$ and $y=-z$ and the corresponding eigenspace is $V_{1}=\operatorname{Span}\left\{\begin{pmatrix} -1 \\ -1 \\ 1 \end{pmatrix}\right\}$.

For $\lambda=2$, the eigenvectors ${\bf v}=\begin{pmatrix} x \\ y \\ z\end{pmatrix}$ satisfy $(A-2I){\bf v}={\bf 0}$: \[\left(\begin{array}{ccc|c} -4 & -2 & -5 & 0 \\ -7 & -5 & -11 & 0 \\ 4 & 2 & 5 & 0 \end{array}\right) \xrightarrow[R_3+R_1]{R_2-2R_1} \left(\begin{array}{ccc|c} -4 & -2 & -5 & 0 \\ 1 & -1 & -1 & 0 \\ 0 & 0 & 0 & 0 \end{array}\right) \xrightarrow[]{R_1-2R_2} \left(\begin{array}{ccc|c} -6 & 0 & -3 & 0 \\ 1 & -1 & -1 & 0 \\ 0 & 0 & 0 & 0 \end{array}\right)\] \[\xrightarrow[]{(-1/3)R_1} \left(\begin{array}{ccc|c} 2 & 0 & 1 & 0 \\ 1 & -1 & -1 & 0 \\ 0 & 0 & 0 & 0 \end{array}\right) \xrightarrow[]{R_2+R_1} \left(\begin{array}{ccc|c} 2 & 0 & 1 & 0 \\ 3 & -1 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{array}\right).\] So $y=3x$ and $z=-2x$ and the corresponding eigenspace is $V_{2}=\operatorname{Span}\left\{\begin{pmatrix} 1 \\ 3 \\ -2 \end{pmatrix}\right\}$.

$(f)\;$ The characteristic polynomial $\det(A-\lambda I)$ is \[\begin{align*} \begin{vmatrix} 5-\lambda & 6 & -2 \\ -1 & -2-\lambda & 3 \\ -1 & -1 & 2-\lambda \end{vmatrix} & \;\;{\overset{R_2-R_3}{\overset{\,}{=}}}\;\; \begin{vmatrix} 5-\lambda & 6 & -2 \\ 0 & -1-\lambda & 1+\lambda \\ -1 & -1 & 2-\lambda \end{vmatrix} \\ & = (-1-\lambda) \begin{vmatrix} 5-\lambda & 6 & -2 \\ 0 & 1 & -1 \\ -1 & -1 & 2-\lambda \end{vmatrix} \\ & \;\;{\overset{C_3+C_2}{\overset{\,}{=}}}\;\; -(1+\lambda) \begin{vmatrix} 5-\lambda & 6 & 4 \\ 0 & 1 & 0 \\ -1 & -1 & 1-\lambda \end{vmatrix} \\ &=-(1+\lambda)\begin{vmatrix} 5-\lambda & 4 \\ -1 & 1-\lambda \end{vmatrix} \\ &=-(\lambda+1)(\lambda-3)^2 \end{align*}\] and so the eigenvalues are $\lambda=-1, 3, 3$.

For $\lambda=-1$, the eigenvectors ${\bf v}=\begin{pmatrix} x \\ y \\ z\end{pmatrix}$ satisfy $(A+I){\bf v}={\bf 0}$: \[ \left(\begin{array}{ccc|c} 6 & 6 & -2 & 0 \\ -1 & -1 & 3 & 0 \\ -1 & -1 & 3 & 0 \end{array}\right) \xrightarrow[R_1+6R_2]{R_3-R_2} \left(\begin{array}{ccc|c} 0 & 0 & 16 & 0 \\ -1 & -1 & 3 & 0 \\ 0 & 0 & 0 & 0 \end{array}\right) \] \[\xrightarrow{(1/16)R_1} \left(\begin{array}{ccc|c} 0 & 0 & 1 & 0 \\ -1 & -1 & 3 & 0 \\ 0 & 0 & 0 & 0 \end{array}\right) \xrightarrow{R_2-3R_1} \left(\begin{array}{ccc|c} 0 & 0 & 1 & 0 \\ -1 & -1 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{array}\right).\]

So $x=-y$ and $z=0$ and the corresponding eigenspace is $V_{-1}=\operatorname{Span}\left\{\begin{pmatrix} 1 \\ -1 \\ 0 \end{pmatrix}\right\}$.

For $\lambda=3$, the eigenvectors ${\bf v}=\begin{pmatrix} x \\ y \\ z\end{pmatrix}$ satisfy $(A-2I){\bf v}={\bf 0}$: \[ \left(\begin{array}{ccc|c} 2 & 6 & -2 & 0 \\ -1 & -5 & 3 & 0 \\ -1 & -1 & -1 & 0 \end{array}\right) \xrightarrow[R_2-R_3]{R_1+2R_3} \left(\begin{array}{ccc|c} 0 & 4 & -4 & 0 \\ 0 & -4 & 4 & 0 \\ -1 & -1 & -1 & 0 \end{array}\right) \xrightarrow{R_1+R_2} \left(\begin{array}{ccc|c} 0 & 0 & 0 & 0 \\ 0 & -4 & 4 & 0 \\ -1 & -1 & -1 & 0 \end{array}\right)\] \[\xrightarrow[-R_3]{(-1/4)R_2} \left(\begin{array}{ccc|c} 0 & 0 & 0 & 0 \\ 0 & 1 & -1 & 0 \\ 1 & 1 & 1 & 0 \end{array}\right) \xrightarrow{R_3-R_2} \left(\begin{array}{ccc|c} 0 & 0 & 0 & 0 \\ 0 & 1 & -1 & 0 \\ 1 & 0 & 2 & 0 \end{array}\right).\] So $x=-2z$ and $y=z$ and the corresponding eigenspace is $\; V_{3}=\operatorname{Span}\left\{\begin{pmatrix} -2 \\ 1 \\ 1 \end{pmatrix}\right\}$.

$(g)\;$ First find eigenvalues: \[\begin{align*} \det(A-\lambda I) &=\begin{vmatrix} 1-\lambda & 1 \\ -2 & -1-\lambda \end{vmatrix} =(1-\lambda)(-1-\lambda)+2 \\ &=\lambda^2+1=(\lambda+i)(\lambda-i) \end{align*}\] so the eigenvalues are $\lambda=\pm i$ (and so the eigenvalues are complex).

For $\lambda=i$, the eigenvectors ${\bf v}=\begin{pmatrix} x \\ y \end{pmatrix}$ satisfy $(A-iI){\bf v}={\bf 0}$: \[\left(\begin{array}{cc|c} 1-i & 1 & 0 \\ -2 & -1-i & 0 \end{array}\right) \xrightarrow{R_2+(1+i)R_1} \left(\begin{array}{cc|c} 1-i & 1 & 0 \\ 0 & 0 & 0\end{array}\right)\] So $(1-i)x+y=0$ and the corresponding eigenspace is $V_{i}=\operatorname{Span}\left\{\begin{pmatrix} -1 \\ 1-i \end{pmatrix}\right\}$.

For $\lambda=-i$, the eigenvectors ${\bf v}=\begin{pmatrix} x \\ y \end{pmatrix}$ satisfy $(A+iI){\bf v}={\bf 0}$: \[\left(\begin{array}{cc|c} 1+i & 1 & 0 \\ -2 & -1+i & 0 \end{array}\right) \xrightarrow{R_2+(1-i)R_1} \left(\begin{array}{cc|c} 1+i & 1 & 0 \\ 0 & 0 & 0 \end{array}\right)\] So $(1+i)x+y=0$ and the corresponding eigenspace is $V_{-i}=\operatorname{Span}\left\{\begin{pmatrix} -1 \\ 1+i \end{pmatrix}\right\}$.

$(h)\;$ The characteristic polynomial $\det(A-\lambda I)$ is \[\begin{align*} \begin{vmatrix} \cos\theta-\lambda & -\sin\theta \\ \sin\theta & \cos\theta-\lambda \end{vmatrix} &=(\cos\theta-\lambda)^2+\sin^2\theta \\ &=\lambda^2-2\lambda\cos\theta+1 \\ &=\lambda^2-\lambda\left(e^{i\theta}+e^{-i\theta}\right)+1 \\ &=\left(\lambda-e^{i\theta}\right)\left(\lambda-e^{-i\theta}\right) \end{align*}\] and so the eigenvalues are $\lambda=e^{\pm i\theta}$, which are not real (since $\theta$ is not a whole multiple of $\pi$).

To find the corresponding eigenspace for $\lambda=e^{i\theta}$, we need to solve $(A-e^{i\theta}I){\bf v}={\bf 0}$.

Notice $\cos\theta-\lambda=\cos\theta-e^{i\theta}=-i\sin\theta$. So we are solving \[ \left(\!\!\begin{array}{cc|c} -i\sin\theta & -\sin\theta & 0 \\ \sin\theta & -i\sin\theta & 0 \end{array}\!\!\right) \xrightarrow[(1/\sin\theta)R_2]{(i/\sin\theta)R_1} \left(\!\!\begin{array}{cc|c} 1 & -i & 0 \\ 1 & -i & 0 \end{array}\!\!\right) \xrightarrow{R_2-R_1} \left(\!\!\begin{array}{cc|c} 1 & -i & 0 \\ 0 & 0 & 0 \end{array}\!\!\right)\] Note here it is okay to divide by $\sin\theta$ since it is non-zero when $\theta$ is not a multiple of $\pi$.

Hence eigenvectors ${\bf v}=\begin{pmatrix} x \\ y \end{pmatrix}$ have $x=iy$ and the corresponding eigenspace is \[V_{e^{i\theta}}=\operatorname{Span}\left\{\begin{pmatrix} i \\ 1 \end{pmatrix}\right\}.\]

Similarly, for $\lambda=e^{-i\theta}$, we need to solve $(A-e^{-i\theta}I){\bf v}={\bf 0}$.

This time, use $\cos\theta-\lambda=\cos\theta-e^{-i\theta}=i\sin\theta$ and \[ \left(\!\!\begin{array}{cc|c} i\sin\theta & -\sin\theta & 0 \\ \sin\theta & i\sin\theta & 0 \end{array}\!\!\right) \xrightarrow[(i/\sin\theta)R_2]{(1/\sin\theta)R_1} \left(\!\!\begin{array}{cc|c} i & -1 & 0 \\ i & -1 & 0 \end{array}\!\!\right) \xrightarrow{R_2-R_1} \left(\!\!\begin{array}{cc|c} i & -1 & 0 \\ 0 & 0 & 0 \end{array}\!\!\right)\] Eigenvectors ${\bf v}=\begin{pmatrix} x \\ y \end{pmatrix}$ have $y=ix$ and the corresponding eigenspace is \[V_{e^{-i\theta}}=\operatorname{Span}\left\{\begin{pmatrix} 1 \\ i \end{pmatrix}\right\}.\]

Question 3.42 $\;$ For each of the following matrices $A$, find an invertible matrix $Y$ such that $D=Y^{-1}AY$ is diagonal and compute $A^{10}$.

$\;\;(a)\;\;A=\begin{pmatrix} 2 & -3 \\ 2 & -5 \end{pmatrix},\hspace{1.8cm}$ $\;\;(b)\;\;A=\begin{pmatrix} 5 & 6 \\ -2 & -2 \end{pmatrix},\hspace{1cm}$ $\;\;(c)\;\;A=\begin{pmatrix} 2 & 3 & 6 \\ 6 & 5 & 12 \\ -3 & -3 & -7 \end{pmatrix},$

$\;\;(d)\;\;A=\begin{pmatrix} -1 & -2 & -4 \\ -4 & -3 & -8 \\ 2 & 2 & 5 \end{pmatrix},\hspace{0.5cm}$ $\;\;(e)\;\;A=\begin{pmatrix} -2 & -2 & -5 \\ -7 & -3 & -11 \\ 4 & 2 & 7 \end{pmatrix}.$

Quick Check

$(a)\;$ $Y=\begin{pmatrix} 1 & 3 \\ 2 & 1 \end{pmatrix}$ and $A^{10}= -\frac{1}{5}\begin{pmatrix} 4^{10}-6 & -3\cdot 4^{10}+3 \\ 2\cdot 4^{10}-2 & -6\cdot 4^{10}+1 \end{pmatrix}$.

$(b)\;$ $Y=\begin{pmatrix} 3 & 2 \\ -2 & -1 \end{pmatrix}$ and $A^{10}=\begin{pmatrix}-3+4\cdot 2^{10} & -6+6\cdot 2^{10} \\2-2\cdot 2^{10} & 4-3\cdot 2^{10} \end{pmatrix}.$

$(c)\;$ $Y=\begin{pmatrix} -1 & -1 & -2 \\ -2 & 1 & 0 \\ 1 & 0 & 1 \end{pmatrix}$ and $A^{10}=\begin{pmatrix} 2^{10} & 2^{10}-1 & 2\cdot 2^{10}-2 \\ 2\cdot 2^{10}-2 & 2\cdot 2^{10}-1 & 4\cdot 2^{10}-4 \\ -2^{10}+1 & -2^{10}+1 & -2\cdot 2^{10}+3 \end{pmatrix}.$

$(d)\;$ $Y=\begin{pmatrix} 1 & -1 & -2 \\ 2 & 1 & 0 \\ -1 & 0 & 1 \end{pmatrix}$ and $A^{10}=\begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix}.$

$(e)\;$ $Y=\begin{pmatrix} 1 & -1 & -1 \\ 3 & -1 & -2 \\ -2 & 1 & 1 \end{pmatrix}$ and $A^{10}=\begin{pmatrix} -2^{10}+2 & 0 &-2^{10}+1\\-3\cdot 2^{10}+3 & 1&-3\cdot 2^{10}+3 \\ 2\cdot 2^{10}-2 & 0 & 2\cdot 2^{10}-1 \end{pmatrix}.$

Solution

$(a)\;$ The characteristic polynomial $\det(A-\lambda I)$ is \[\begin{align*} \begin{vmatrix} 2-\lambda & -3 \\ 2 & -5-\lambda \end{vmatrix} &=(2-\lambda)(-5-\lambda)+6 \\ &=\lambda^2+3\lambda-4=(\lambda+4)(\lambda-1) \end{align*}\] so the eigenvalues are $\lambda=-4,1$.

For $\lambda=-4$, find ${\bf v}=\begin{pmatrix} x \\ y \end{pmatrix}$ satisfying $(A+4I){\bf v}={\bf 0}$: \[\left(\begin{array}{cc|c} 6 & -3 & 0 \\ 2 & -1 & 0 \end{array}\right) \xrightarrow{\frac{1}{3}R_1} \left(\begin{array}{cc|c} 2 & -1 & 0 \\ 2 & -1 & 0 \end{array}\right) \xrightarrow{R_2-R_1} \left(\begin{array}{cc|c} 2 & -1 & 0 \\ 0 & 0 & 0 \end{array}\right).\] So $2x-y=0$ and a corresponding eigenvector is ${\bf v}=\begin{pmatrix} 1 \\ 2 \end{pmatrix}$.

For $\lambda=1$, find ${\bf v}=\begin{pmatrix} x \\ y \end{pmatrix}$ satisfying $(A-I){\bf v}={\bf 0}$: \[\left(\begin{array}{cc|c} 1 & -3 & 0 \\ 2 & -6 & 0 \end{array}\right) \xrightarrow{\frac{1}{2}R_2} \left(\begin{array}{cc|c} 1 & -3 & 0 \\ 1 & -3 & 0 \end{array}\right) \xrightarrow{R_2-R_1} \left(\begin{array}{cc|c} 1 & -3 & 0 \\ 0 & 0 & 0 \end{array}\right).\] So $x-3y=0$ and a corresponding eigenvector is ${\bf v}=\begin{pmatrix} 3 \\ 1 \end{pmatrix}$.

Hence, $Y^{-1}AY=D$, where \[Y=\begin{pmatrix} 1 & 3 \\ 2 & 1 \end{pmatrix}\qquad\text{and}\qquad D=\begin{pmatrix} -4 & 0 \\ 0 & 1 \end{pmatrix}.\] Then \[\begin{align*} A^{10}&=(YDY^{-1})^{10}=YD^{10}Y^{-1} \\ &= \begin{pmatrix} 1 & 3 \\ 2 & 1 \end{pmatrix} \begin{pmatrix} 4^{10} & 0 \\ 0 & 1 \end{pmatrix} \frac{1}{-5}\begin{pmatrix} 1 & -3 \\ -2 & 1 \end{pmatrix} \\ &=-\frac{1}{5}\begin{pmatrix} 1 & 3 \\ 2 & 1 \end{pmatrix} \begin{pmatrix} 4^{10} & -3\cdot 4^{10} \\ -2 & 1 \end{pmatrix}\\ &= -\frac{1}{5}\begin{pmatrix} 4^{10}-6 & -3\cdot 4^{10}+3 \\ 2\cdot 4^{10}-2 & -6\cdot 4^{10}+1 \end{pmatrix}. \end{align*}\]

$(b)\;$ Working in the same way, $A$ has eigenvalues 1, 2 with corresponding eigenvectors $\begin{pmatrix} 3 \\ -2 \end{pmatrix}$ and $\begin{pmatrix} 2 \\ -1 \end{pmatrix}$ so we may take \[Y=\begin{pmatrix} 3 & 2 \\ -2 & -1 \end{pmatrix}\qquad\text{and}\qquad D=\begin{pmatrix} 1 & 0 \\ 0 & 2 \end{pmatrix}.\] Then \[\begin{align*} A^{10}=YD^{10}Y^{-1} &= \begin{pmatrix} 3 & 2 \\ -2 & -1 \end{pmatrix} \begin{pmatrix} 1 & 0 \\ 0 & 2^{10} \end{pmatrix} \begin{pmatrix} -1 & -2 \\ 2 & 3 \end{pmatrix} \\ &= \begin{pmatrix} -3+4\cdot 2^{10} & -6+6\cdot 2^{10} \\ 2-2\cdot 2^{10} & 4-3\cdot 2^{10} \end{pmatrix}. \end{align*}\]

$(c)\;$ The eigenvalues are $2$, $-1$, $-1$ with (choices of) corresponding eigenvectors forming the columns of \[Y=\begin{pmatrix} -1 & -1 & -2 \\ -2 & 1 & 0 \\ 1 & 0 & 1 \end{pmatrix}\] and \[Y^{-1}AY=D=\begin{pmatrix} 2 & 0 & 0 \\ 0 & -1 & 0 \\ 0 & 0 & -1 \end{pmatrix}.\] Hence \[\begin{align*} A^{10}&=YD^{10}Y^{-1} \\ &=\begin{pmatrix} -1 & -1 & -2 \\ -2 & 1 & 0 \\ 1 & 0 & 1 \end{pmatrix} \begin{pmatrix} 2^{10} & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} -1 & -1 & -2 \\ -2 & -1 & -4 \\ 1 & 1 & 3 \end{pmatrix} \\ &=\begin{pmatrix} 2^{10} & 2^{10}-1 & 2\cdot 2^{10}-2 \\ 2\cdot 2^{10}-2 & 2\cdot 2^{10}-1 & 4\cdot 2^{10}-4 \\ -2^{10}+1 & -2^{10}+1 & -2\cdot 2^{10}+3 \end{pmatrix}. \end{align*}\]

$(d)\;$ The eigenvalues are $-1$, $1$, $1$ with (choices of) corresponding eigenvectors forming the columns of \[Y=\begin{pmatrix} 1 & -1 & -2 \\ 2 & 1 & 0 \\ -1 & 0 & 1 \end{pmatrix}\] and \[Y^{-1}AY=D=\begin{pmatrix} -1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix}.\] Notice that $D^{10}=I$ and so we can actually find $A^{10}$ without knowing $Y$: \[A^{10}=YD^{10}Y^{-1}=YY^{-1}=I= \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix}.\]

$(e)\;$ The eigenvalues are $2$, $1$, $-1$ with (choices of) corresponding eigenvectors forming the columns of \[Y=\begin{pmatrix} 1 & -1 & -1 \\ 3 & -1 & -2 \\ -2 & 1 & 1 \end{pmatrix}\] and \[Y^{-1}AY=D=\begin{pmatrix} 2 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & -1 \end{pmatrix}.\] Hence \[\begin{align*} A^{10}&=YD^{10}Y^{-1} \\ &=\begin{pmatrix} 1 & -1 & -1 \\ 3 & -1 & -2 \\ -2 & 1 & 1 \end{pmatrix} \begin{pmatrix} 2^{10} & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} -1 & 0 & -1 \\ -1 & 1 & 1 \\ -1 & -1 & -2 \end{pmatrix} \\ &=\begin{pmatrix} -2^{10}+2 & 0 & -2^{10}+1 \\ -3\cdot 2^{10}+3 & 1 & -3\cdot 2^{10}+3 \\ 2\cdot 2^{10}-2 & 0 & 2\cdot 2^{10}-1 \end{pmatrix}. \end{align*}\]

Question 3.43 $\;$

$\;\;(a)\;\;$ Find a matrix $B$ satisfying $B^3=A$ where $A=\begin{pmatrix} 97 & -70 \\ 105 & -78 \end{pmatrix}$.

$\;\;(b)\;\;$ Find a matrix $B$ satisfying $B^5=A$ where $A=\begin{pmatrix} -67 & 198 \\ -33 & 98 \end{pmatrix}$.

Quick Check

$(a)\;$ $B= \begin{pmatrix} 13 & -10 \\ 15 & -12 \end{pmatrix}$, $\hspace{2cm}$ $(b)\;$ $B= \begin{pmatrix} -7 & 18 \\ -3 & 8 \end{pmatrix}$

Solution

$(a)\;$ First diagonalise: $Y^{-1}AY=D$ where \[Y=\begin{pmatrix} 2 & 1 \\ 3 & 1 \end{pmatrix}\qquad\text{and}\qquad D=\begin{pmatrix} -8 & 0 \\ 0 & 27 \end{pmatrix}.\] Then $\;C=\begin{pmatrix} -2 & 0 \\ 0 & 3 \end{pmatrix}\;$ satisfies $C^3=D$. Hence \[\begin{align*} B=YCY^{-1}&=\begin{pmatrix} 2 & 1 \\ 3 & 1 \end{pmatrix} \begin{pmatrix} -2 & 0 \\ 0 & 3 \end{pmatrix} \begin{pmatrix} -1 & 1 \\ 3 & -2 \end{pmatrix}\\ &= \begin{pmatrix} 13 & -10 \\ 15 & -12 \end{pmatrix} \end{align*}\] satisfies $\;B^3=\left(YCY^{-1}\right)^3=YC^3Y^{-1}=YDY^{-1}=A$.

$(b)\;$ First diagonalise: $Y^{-1}AY=D$ where \[Y=\begin{pmatrix} 2 & 3 \\ 1 & 1 \end{pmatrix}\qquad\text{and}\qquad D=\begin{pmatrix} 32 & 0 \\ 0 & -1 \end{pmatrix}.\] Then $\; C=\begin{pmatrix} 2 & 0 \\ 0 & -1 \end{pmatrix}\;$ satisfies $C^5=D$. Hence \[\begin{align*} B=YCY^{-1}&=\begin{pmatrix} 2 & 3 \\ 1 & 1 \end{pmatrix} \begin{pmatrix} 2 & 0 \\ 0 & -1 \end{pmatrix} \begin{pmatrix} -1 & 3 \\ 1 & -2 \end{pmatrix}\\ &= \begin{pmatrix} -7 & 18 \\ -3 & 8 \end{pmatrix} \end{align*}\] satisfies $\;B^5=\left(YCY^{-1}\right)^5=YC^5Y^{-1}=YDY^{-1}=A$.

Question 3.44 $\;$ Consider the triangular matrix $A=\begin{pmatrix} a & b \\ 0 & d \end{pmatrix}$. Find necessary and sufficient conditions on the entries $a$, $b$, $d$ so that $A$ is not diagonalisable.

Quick Check

$A$ is not diagonalisable precisely when $a=d$ and $b\neq 0$.

Solution

If a $2\times 2$ matrix has two distinct eigenvalues then it is automatically diagonalisable. Suppose that $A$ is not diagonalisable. Then the characteristic polynomial \[\begin{vmatrix} a-\lambda & b \\ 0 & d-\lambda \end{vmatrix} =(a-\lambda)(d-\lambda)\] must have equal roots and so $\lambda=a=d$.

Also, if $b=0$ then the matrix is already diagonal, so suppose $a=d$ and $b\neq 0$. To find eigenvectors we solve $(A-\lambda I){\bf v}=\boldsymbol{0}$, i.e. \[\begin{pmatrix} 0 & b \\ 0 & 0 \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix}= \begin{pmatrix} 0 \\ 0 \end{pmatrix} \quad\implies\quad bx=0 \quad\implies\quad x=0. \] The eigenspace is $\operatorname{Span}\left\{\begin{pmatrix} 0 \\ 1 \end{pmatrix}\right\}$ and there can’t be a basis of eigenvectors. Hence, $A$ is not diagonalisable precisely when $a=d$ and $b\neq 0$.

For a trickier challenge, you could try the same question for a general $2\times 2$ matrix \[A=\begin{pmatrix} a & b \\ c & d \end{pmatrix}.\]