1.7. Lecture 7

1.7.1. Topological properties: answer to question (2)

We now turn to the second question, whether every Lie algebra homomorphism exponentiates to a Lie group homomorphism. In the light of what we have seen, it is sensible to restrict to the case of connected Lie groups. However, even with this restriction, the answer is in general no, as the next example shows!

Example 1.7.1.

The linear Lie groups $\operatorname{GL}_{1}^{+}(\mathbb{R})=\mathbb{R}_{>0}$ and $U(1)=\{z\in\mathbb{C}\,|\,|z|=1\}$ both have Lie algebra $\mathbb{R}$ with trivial Lie bracket; in the second case we get the subspace $i\mathbb{R}\subseteq\mathbb{C}$ of $\mathfrak{gl}_{2,\mathbb{C}}$ and identify it with $\mathbb{R}$ by dividing by $i$ .

The Lie algebra homomorphisms $\mathbb{R}\to\mathbb{R}$ are all of the form $\phi_{a}:t\mapsto at$ for some $a\in\mathbb{R}$ . We consider which of these exponentiate to homomorphisms of Lie groups.

(i)

The map $\phi_{a}$ always exponentiates to a map $\mathbb{R}_{>0}\to\mathbb{R}_{>0}$ , specifically the map

$x\longmapsto e^{ax}.$
(ii)

The map $\phi_{a}$ always exponentiates to a map $\mathbb{R}_{>0}\to U(1)$ , specifically the map

$x\longmapsto e^{iax}.$
(iii)

The map $\phi_{a}$ never exponentiates to a map $U(1)\to\mathbb{R}_{>0}$ if $a\neq 0$ . If it did, the map would have to send

$e^{ix}\longmapsto e^{ax},$

and setting $x=2\pi$ gives $a=0$ .
(iv)

The map $\phi_{a}$ exponentiates to a map $U(1)\to U(1)$ if and only if $a\in\mathbb{Z}$ , in which case the map is

$z\longmapsto z^{a}.$

Indeed, the map would have to be

$e^{ix}\longrightarrow e^{iax}$

and setting $x=2\pi$ shows that $a\in\mathbb{Z}$ , when the map is as claimed.

The key difference between $\mathbb{R}_{>0}$ and $U(1)$ is that the former is simply connected while the latter is not (it has fundamental group $\mathbb{Z}$ ). We explain this a bit further.

Recall we call a topological/metric space $X$ simply connected if it is path-connected and if every loop can be continuous shrunk to a single point; rigorously, if every continuous map from the unit circle to $X$ can be extended to a continuous map from the unit disc to $X$ . In topology, the failure of a space to be simply connected is measured by the ‘fundamental group’ $\pi_{1}(X)$ : $X$ is simply-connected if and only if $\pi_{1}(X)$ is trivial.

Theorem 1.7.2.

Let $G$ be a simply connected (linear) Lie group. Let $G^{\prime}$ be any other (linear) Lie group. Let $\mathfrak{g}$ and $\mathfrak{g}^{\prime}$ be their Lie algebras. Then every homomorphism $\mathfrak{g}\rightarrow\mathfrak{g}^{\prime}$ exponentiates to a unique homomorphism $G\rightarrow G^{\prime}$ .

Hence we have a 1-1 correspondence

\{\operatorname{Hom}(G,G^{\prime})\}\quad\longleftrightarrow\quad\{% \operatorname{Hom}(\mathfrak{g},\mathfrak{g}^{\prime})\}.

Proof.

This is beyond the scope of this course. Note in the above example $\operatorname{GL}_{1}^{+}(\mathbb{R})$ is simply connected while the circle group $U(1)$ is not. ∎

One can show that $\operatorname{SL}_{n}(\mathbb{C})$ and $\mathrm{SU}(n)$ are simply connected. Here is a small table showing our connected groups and their fundamental groups.

$G$	$\pi_{1}(G)$
$\operatorname{GL}_{n}(\mathbb{C})$	$\mathbb{Z}$
$\operatorname{SL}_{n}(\mathbb{C})$	$1$
$\operatorname{SL}_{2}(\mathbb{R})$	$\mathbb{Z}$
$\operatorname{SL}_{n}(\mathbb{R})$ , $n\geq 3$	$C_{2}$
$\mathrm{SO}(2)$	$\mathbb{Z}$
$\mathrm{SO}(n)$ , $n\geq 3$	$C_{2}$
$\operatorname{U}(n)$	$\mathbb{Z}$
$\mathrm{SU}(n)$	$1$
$\mathrm{Sp}(2n)$	$Z$

Remark 1.7.3.

It is not an accident that the fundamental groups of $\operatorname{SL}_{n}(\mathbb{R})$ and $\mathrm{SO}(n)$ are isomorphic — Gram–Schmidt orthogonalisation, as used in the proof of Proposition 1.6.9, shows that $\operatorname{SL}_{n}(\mathbb{R})$ and $\mathrm{SO}(n)$ are homotopy equivalent. A similar remark applies to $\operatorname{SL}_{n}(\mathbb{C})$ and $\mathrm{SU}(n)$ .

If $G$ is not connected, or its identity component is not simply connected, we can work in the following way.

•

There exists a ’universal cover’ $\widetilde{G}$ of $G^{0}$ which is simply connected, and also has the structure of a Lie group (not necessarily linear, unfortunately). There is a surjective group homomorphism $\pi:\widetilde{G}\to G^{0}$ with discrete kernel $Z\cong\pi_{1}(G^{0})$ , so that $G^{0}\cong\widetilde{G}/Z$ .
•

The kernel $Z$ of $\pi$ is isomorphic to the fundamental group $\pi_{1}(G^{0})$ .
•

Homomorphisms out of $G^{0}$ are in 1-1 correspondence with homomorphisms out of $\widetilde{G}$ which are trivial on $Z$ .
•

The Lie algebras of $G$ , $G^{0}$ and $\widetilde{G}$ coincide (more precisely, the maps $\pi:\widetilde{G}\to G^{0}$ and $\iota:G^{0}\to G$ induce isomorphisms of Lie algebras).
•

In general $G/G^{0}$ can be an arbitrary finite group! For this reason, it is common to restrict attention to connected Lie groups.

The diagram looks as follows:

\begin{CD}\mathfrak{g}@>{\exp}>{}>\widetilde{G}\\ \Big{\|}@V{}V{\pi}V\\ \mathfrak{g}@>{}>{\exp}>G^{0}@>{\iota}>{}>G.\end{CD}

Example 1.7.4.

The group $U(1)$ is not simply connected. Here the universal cover is $(\mathbb{R},+)$ (this is a linear Lie group because it is isomorphic to the upper triangular $2\times 2$ matrices with $1$ s on the diagonal — a similar argument shows that any vector space (with addition) is a Lie group). The map $\widetilde{G}\to G^{0}$ is then

	$\displaystyle\pi:\mathbb{R}$	$\displaystyle\longrightarrow U(1)$
	$\displaystyle x$	$\displaystyle\longmapsto e^{2\pi ix}$

and we see that the kernel of $\pi$ is $\mathbb{Z}$ , which is indeed the fundamental group $\pi_{1}(U(1))$ .

1.7.2. The example of $SU(2)$ and $SO(3)$

We illustrate the previous section with the example of $\mathrm{SO}(3)$ . According to the table of fundamental groups above, the fundamental group of $\mathrm{SO}(3)$ is $C_{2}$ . We can visualise this as follows: An element of $\mathrm{SO}(3)$ is rotation by some angle $\theta\in[0,\pi]$ about some (oriented) axis. We can represent this as a vector in $\mathbb{R}^{3}$ of length $\theta$ in the direction of the axis. Elements of $\mathrm{SO}(3)$ then correspond to points in the closed ball in $\mathbb{R}^{3}$ of radius $2\pi$ . However, rotation by $\pi$ about the axis ${\bf v}$ is the same as rotation by $\pi$ about the axis $-\pi$ , and so we must identify diametrically opposite points on the boundary of this ball.

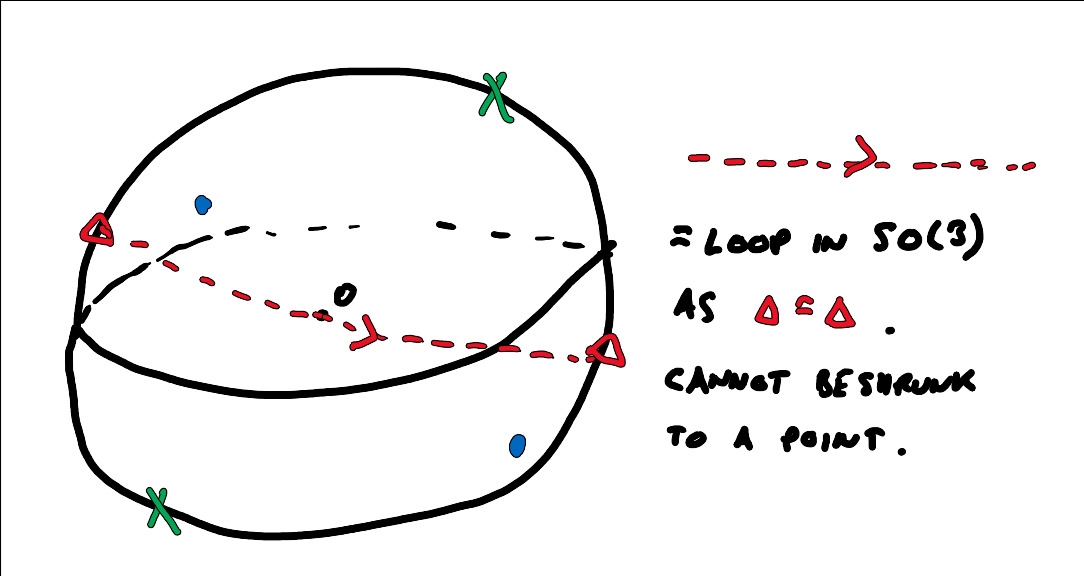
Refer to caption — Figure 1.2. Picture of $\mathrm{SO}(3)$

Now, the straight line in this three-dimensional sphere from a point on the boundary to its diametrically opposite point is a loop in $\mathrm{SO}(3)$ since the endpoints represent the same rotation. You can convince yourself that this loop cannot be shrunk to a point (proving it rigorously requires some topology). However, if you go around the loop twice, then that can (!) be shrunk to a point. The idea is to move one copy of the loop out to the boundary, then use the ‘opposite point’ identification to move it to the other side, when you get a normal loop inside the ball which may be shrunk. See Figure 1.3.

A nice physical illustration of this is provided by the “Dirac belt trick”; here is a video of this demonstrated with long hair!

According to the general picture of the previous section, there should be a Lie group homomorphism $\tilde{G}\to\mathrm{SO}(3)$ whose kernel has order 2 and such that $\tilde{G}$ is simply connected, and it turns out that we can take $\tilde{G}=\mathrm{SU}(2)$ . So we study this group for a bit.

Firstly, one can show (see problem 1.7.3) that every element of $\mathrm{SU}(2)$ has the form

\begin{pmatrix}a&-\overline{b}\\ b&\overline{a}\end{pmatrix}

for $a,b\in\mathbb{C}$ with $|a|^{2}+|b|^{2}=1$ . It follows that $\mathrm{SU}(2)$ is diffeomorphic to the unit sphere $S^{3}$ in $\mathbb{R}^{4}$ , which is simply connected.

We would like to write down a homomorphism $\mathrm{SU}(2)\to\mathrm{SO}(3)$ . For this, we want to find a three-dimensional real vector space $V$ , equipped with an inner product (i.e. a positive definite, symmetric, bilinear form) that is preserved by the action of $\mathrm{SU}(2)$ . If we write down an orthonormal basis for $V$ , then the matrix of the action of each element of $\mathrm{SU}(2)$ on $V$ , with respect to this basis, will be an element of $\mathrm{SO}(3)$ giving the required homomorphism.

Where can we find $V$ ? From $\mathrm{SU}(2)$ itself! We take $V=\mathfrak{su}_{2}$ , a three-dimensional vector space (by problem 1.4.2), and let $\mathrm{SU}(2)$ act on $V$ via conjugation. We just need an inner product, and we may define one as follows: for $X,Y\in\mathfrak{su}_{2}$ , let

\left\langle X,Y\right\rangle:=-\operatorname{tr}(XY).

The proof this is an inner product is Problem 1.7.3. We therefore obtain a homomorphism $\pi:\mathrm{SU}(2)\to\mathrm{SO}(3)$ once we fix an orthonormal basis with respect to the inner product. The basis elements may be taken to be the matrices

\frac{1}{\sqrt{2}}\begin{pmatrix}i&0\\ 0&-i\end{pmatrix},\frac{1}{\sqrt{2}}\begin{pmatrix}0&1\\ -1&0\end{pmatrix},\frac{1}{\sqrt{2}}\begin{pmatrix}0&i\\ i&0\end{pmatrix}.

It is an exercise to check that it has the right kernel, i.e. $\ker\pi=C_{2}$ .

1.7.3. Exercises

Problem 16. Check that the Lie algebra of $\mathrm{SO}(2)$ is also isomorphic to $\mathbb{R}$ . Write down an isomorphism $U(1)\to\mathrm{SO}(2)$ ; what is the identification of Lie algebras it induces?

Problem 17. Show that a general element of $\mathrm{SU}(2)$ may be written

\begin{pmatrix}a&-\overline{b}\\ b&\overline{a}\end{pmatrix}

for $a,b\in\mathbb{C}$ with $|a|^{2}+|b|^{2}=1$ .

Deduce that $\mathrm{SU}(2)$ is diffeomorphic to the three-sphere $S^{3}=\{v\in\mathbb{R}^{4}\,|\,|v|=1\}$ .

In other words, write down a smooth bijection $\mathrm{SU}(2)\rightarrow S^{3}$ with smooth inverse. Don’t worry about checking that the maps are smooth, just write them down. The result of this problem implies that $\mathrm{SU}(2)$ is simply-connected.

Problem 18.

(a)

Show that $\left\langle\cdot,\cdot\right\rangle$ is a symmetric, positive definite bilinear form on $\mathfrak{su}_{2}$ .
(b)

Show that it is preserved by the action of $\mathrm{SU}(2)$ , i.e. that

$\left\langle gXg^{-1},gYg^{-1}\right\rangle=\left\langle X,Y\right\rangle$

for all $g\in\mathrm{SU}(2)$ .

Problem 19. Write down explicitly the image of $\begin{pmatrix}a&-\overline{b}\\ b&\overline{a}\end{pmatrix}$ under the homomorphism $\pi$ .

Problem 20. Show that, if $g\in\mathrm{SU}(2)$ satisfies $gXg^{-1}=X$ for all $X\in\mathfrak{su}_{2}$ , then $g=\pm\operatorname{Id}$ . Deduce that

\ker(\pi)=\{\pm\operatorname{Id}\}\cong C_{2}.

Problem 21. If $\mathfrak{g}$ is a Lie algebra, let $\mathfrak{z}$ be its centre:

\mathfrak{z}=\{Z\in\mathfrak{g}\,|\,[X,Z]=0,\,\forall X\in\mathfrak{g}.\}.

Suppose that $G$ is a connected Lie group with centre $Z$ and Lie algebra $\mathfrak{g}$ with centre $\mathfrak{z}$ .

Prove that $\mathfrak{z}$ is the Lie algebra of $Z$ .