4.19. Lecture 19

4.19.1. Highest weights

We now develop the theory of highest weights, analogous to that for $\mathfrak{sl}_{2,\mathbb{C}}$ . We first carry out the fundamental weight calculation (the analogue of Lemma 3.13.1).

Lemma 4.19.1.

(Fundamental Weight Calculation). Let $V$ be a representation of $\mathfrak{sl}_{3,\mathbb{C}}$ and let ${\bf v}\in V_{\beta}$ be a weight vector with weight $\beta\in\mathfrak{h}^{*}$ . Let $\alpha\in\mathfrak{h}^{*}$ be a root and let $X_{\alpha}\in\mathfrak{g}_{\alpha}$ be a root vector. Then

X_{\alpha}({\bf v})\in V_{\alpha+\beta}.

Thus we obtain a map

X_{\alpha}:V_{\beta}\longrightarrow V_{\alpha+\beta}.

Proof.

Let $H\in\mathfrak{h}$ . Then

H(X({\bf v}))=([H,X]+XH)({\bf v})=\alpha(H)X({\bf v})+X(\beta(H){\bf v})=(% \alpha+\beta)(H)X({\bf v}).\qed

Example 4.19.2.

We work this out for the adjoint representation. Recall that, for $i\neq j$ , we have the root $\alpha_{ij}=L_{i}-L_{j}$ with root vector $E_{ij}$ . The above calculation shows that, if $\alpha$ and $\beta$ are roots, then $[\mathfrak{g}_{\alpha},\mathfrak{g}_{\beta}]\subseteq\mathfrak{g}_{\alpha+\beta}$ . Here are some examples:

(i)

If $\alpha=\alpha_{12}$ , $\beta=\alpha_{13}$ , then $\alpha+\beta$ is not a root so $\mathfrak{g}_{\alpha+\beta}=0$ . Thus $[E_{12},E_{23}]=0$ (which could also be checked directly).
(ii)

If $\alpha=-\beta$ then we get

$[\mathfrak{g}_{\alpha},\mathfrak{g}_{-\alpha}]\subseteq\mathfrak{g}_{0}=% \mathfrak{h}.$
(iii)

If $\alpha=\alpha_{12}$ , $\beta=\alpha_{23}$ , then $\alpha+\beta=\alpha_{13}$ and we get

$[E_{12},E_{23}]\in\mathfrak{g}_{\alpha_{13}}=\left\langle E_{13}\right\rangle.$

In fact, you can check that $[E_{12},E_{23}]=E_{13}$ .

Corollary 4.19.3.

Let $V$ be a finite-dimensional irreducible representation of $\mathfrak{sl}_{3,\mathbb{C}}$ . Then the weights occurring in $V$ all differ by integral linear combinations of the roots of $\mathfrak{sl}_{3,\mathbb{C}}$ , that is, by integral linear combinations of $L_{i}-L_{j}$ .

Proof.

Let $\alpha$ be any weight of $V$ . Then the weights obtained by (repeatedly) applying elements of $\mathfrak{sl}_{3,\mathbb{C}}$ differ by integral linear combinations of the roots. On the other hand this also gives an invariant subspace, which by irreducibility is all of $V$ . ∎

With regard to the weight diagram, we observe that the positive root vectors $E_{12}$ , $E_{23}$ , $E_{13}$ move in the ‘north-east’ direction while the negative root vectors move in the ‘south-west’ direction (roughly speaking). See Figure 4.3.

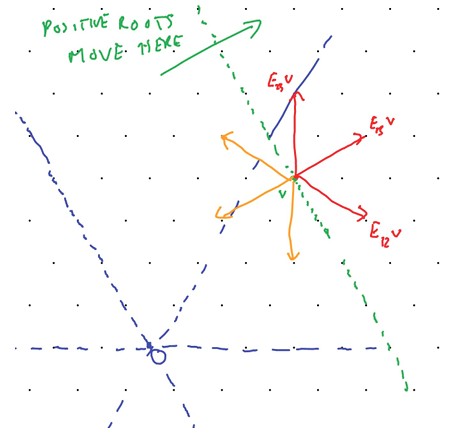
Refer to caption — Figure 4.3. Effect of roots

Definition 4.19.4.

Let $(\rho,V)$ be a representation of $\mathfrak{sl}_{3,\mathbb{C}}$ . A highest weight vector in $V$ is a vector ${\bf v}\in V$ such that:

(i)

${\bf v}$ is a weight vector; and
(ii)

$\rho(E_{12}){\bf v}=\rho(E_{23}){\bf v}=0$ .

The weight of ${\bf v}$ is then a highest weight for $V$ .

Remark 4.19.5.

Since $[E_{12},E_{23}]=E_{13}$ , it follows also that $E_{13}{\bf v}=0$ for ${\bf v}$ a highest weight vector. So all positive root vectors send ${\bf v}$ to $0$ .

Example 4.19.6.

(i)

The standard representation $V$ has highest weight $L_{1}$ with highest weight vector ${\bf e}_{1}$ .
(ii)

The dual $V^{*}$ has highest weight $-L_{3}$ with highest weight vector ${\bf e}_{3}^{*}$ .
(iii)

The adjoint representation has highest weight $L_{1}-L_{3}$ with highest weight vector $E_{13}$ .
(iv)

The symmetric square $\operatorname{Sym}^{2}(\mathbb{C}^{3})$ has highest weight $2L_{1}$ with highest weight vector ${\bf e}_{1}^{2}$ .

Lemma 4.19.7.

Let $V$ be a finite-dimensional representation of $\mathfrak{sl}_{3,\mathbb{C}}$ . Then $V$ has a highest weight vector.

Proof.

For a weight $\alpha=\alpha_{1}L_{1}+\alpha_{1}L_{2}+\alpha_{3}L_{3}$ , define $l(\alpha)=\alpha_{1}-\alpha_{3}$ . Of all the finitely many weights of $V$ , choose a weight $\alpha$ such that $l(\alpha)$ is maximal.

Let ${\bf v}$ be a weight vector with this weight. Then $E_{12}{\bf v}$ , if non-zero, has weight $\alpha+L_{1}-L_{2}$ and

l(\alpha+L_{1}-L_{2})=l(\alpha)+l(L_{1}-L_{2})=l(\alpha)+1>l(\alpha).

This is not a weight of $V$ by maximality of $l(\alpha)$ . Thus $E_{12}{\bf v}=0$ . Similarly $E_{23}{\bf v}$ , if non-zero, has weight $\alpha+L_{2}-L_{3}$ and $l(\alpha+L_{2}-L_{3})=l(\alpha)+1$ , so $E_{23}{\bf v}=0$ . ∎

4.19.2. Weyl symmetry

Let $s_{1}$ , $s_{2}$ , and $s_{3}$ be, respectively, reflections in the lines through $L_{1}$ , $L_{2}$ , and $L_{3}$ . Then any two of these (say $s_{1}$ and $s_{3}$ ) generate the Weyl group $W$ , which is the group of symmetries of the triangle with vertices $L_{1},L_{2},L_{3}$ . So we have $W\cong D_{3}\cong S_{3}$ . Note that $W$ acts on the plane in a way that preserves the weight lattice. See Figure 4.4.

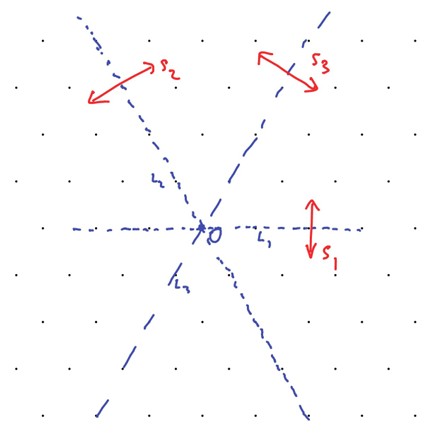
Theorem 4.19.8.

Let $(\rho,V)$ be a finite-dimensional representation of $\mathfrak{sl}_{3,\mathbb{C}}$ . Then the weights of $V$ are symmetric with respect to the action of the Weyl group.

Proof.

We will prove they are symmetric with respect to $s_{3}$ by using the inclusion

\iota=\iota_{12}:\mathfrak{sl}_{2,\mathbb{C}}\rightarrow\mathfrak{sl}_{3,% \mathbb{C}}

that puts a $2\times 2$ matrix in the top left corner of a $3\times 3$ matrix. We consider the restriction of $V$ to $\mathfrak{sl}_{2,\mathbb{C}}$ .

Note that if ${\bf v}\in V$ is a weight vector with weight $aL_{1}-bL_{3}$ , then

\rho(\iota(H)){\bf v}=\rho\left(\begin{pmatrix}1&&\\ &-1&\\ &&0\end{pmatrix}\right){\bf v}=a{\bf v}.

Thus ${\bf v}$ is an $\mathfrak{sl}_{2,\mathbb{C}}$ -weight vector with weight $a$ . Note that $\iota(X)=E_{12}$ , so an $\mathfrak{sl}_{2,\mathbb{C}}$ -weight vector in $V$ is an $\mathfrak{sl}_{2,\mathbb{C}}$ -highest weight vector if it is sent to $0$ under the action of $E_{12}$ .

The kernel of $E_{12}$ on $V$ is preserved by $\mathfrak{h}$ (check this, Problem 4.19.3) and so has a basis made up of $\mathfrak{sl}_{3,\mathbb{C}}$ -weight vectors ${\bf v}_{1},\ldots,{\bf v}_{r}$ . These are then a maximal set of linearly independent highest weight vectors for $\mathfrak{sl}_{2,\mathbb{C}}$ and in particular, if $V_{i}$ is the $\mathfrak{sl}_{2,\mathbb{C}}$ -representation generated by ${\bf v}_{i}$ then, as an $\mathfrak{sl}_{2,\mathbb{C}}$ -representation,

V=\bigoplus_{i=1}^{r}V_{i}.

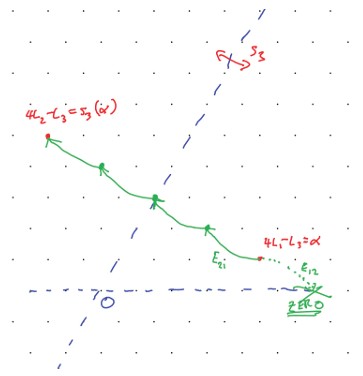
Fix $i$ ; it suffices to show that $V_{i}$ has a basis of $\mathfrak{sl}_{3,\mathbb{C}}$ -weight vectors whose weights are preserved by $s_{3}$ . Let ${\bf v}_{i}$ have weight $aL_{1}-bL_{3}$ . It follows from the $\mathfrak{sl}_{2,\mathbb{C}}$ -theory that $a\geq 0$ and — remembering that $\iota(Y)=E_{21}$ — that $V_{i}$ has a basis

{\bf v},E_{21}{\bf v},\ldots,E_{21}^{a}{\bf v}.

By the FWC (Lemma 4.19.1) we see that these are weight vectors with weights

aL_{1}-bL_{3},(a-1)L_{1}+L_{2}-bL_{3},\ldots,L_{1}+(a-1)L_{2}-bL_{3},aL_{2}-bL% _{3}

which are symmetrical under $s_{3}$ (this reflection swaps $L_{1}$ and $L_{2}$ ), as required. This argument is illustrated in Figure 4.5.

Invariance with respect to the other reflections is proved similarly using the other inclusions $\iota_{ij}$ of $\mathfrak{sl}_{2,\mathbb{C}}$ in $\mathfrak{sl}_{3,\mathbb{C}}$ . ∎

Corollary 4.19.9.

Every highest weight is of the form $aL_{1}-bL_{3}$ for $a,b\geq 0$ integers.

Proof.

Indeed, in the course of the proof of Theorem 4.19.8 we showed that if $aL_{1}-bL_{3}$ was a highest weight, then $a\geq 0$ . A similar argument shows that $b\geq 0$ . ∎

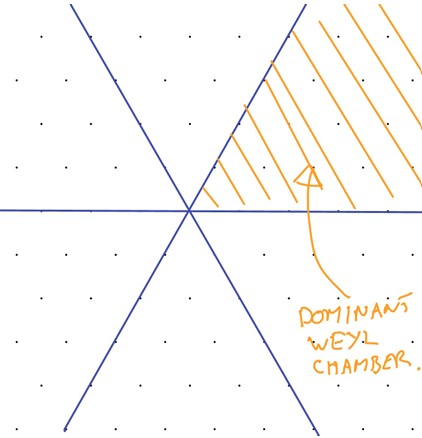
Definition 4.19.10.

The region

\{aL_{1}-bL_{3}\,|\,a,b\in\mathbb{R}_{\geq 0}\}

is called the dominant Weyl chamber and weights inside it (including the boundary) are dominant weights.

4.19.3. Exercises

Problem 54. Show that the kernel of $E_{12}$ is preserved by $\mathfrak{h}$ .

Problem 55. Let $(\rho,V)$ is a representation of $\mathfrak{sl}_{3,\mathbb{C}}$ . As $\operatorname{SL}_{3}(\mathbb{C})$ is simply-connected $\rho$ exponentiates to a representation, $\tilde{\rho}$ , of $\operatorname{SL}_{3}(\mathbb{C})$ . Let

\sigma_{3}=\begin{pmatrix}0&1&0\\ -1&0&0\\ 0&0&1\end{pmatrix}\in\operatorname{SL}_{3}(\mathbb{C}).

(i)

Show that, for every weight $\alpha$ , $\tilde{\rho}(\sigma_{3})$ is an isomorphism

$V_{\alpha}\rightarrow V_{s_{3}\alpha}.$

Here $s_{3}(a_{1}L_{1}+a_{2}L_{2}+a_{3}L_{3})=a_{1}L_{2}+a_{2}L_{1}+a_{3}L_{3}$ .
(ii)

Give another proof of Theorem 4.19.8.

Problem 56. Let $a,b\geq 0$ be integers. Check that

{\bf e}_{1}^{a}\otimes({\bf e}_{3}^{*})^{b}\in\operatorname{Sym}^{a}(\mathbb{C% }^{3})\otimes\operatorname{Sym}^{b}((\mathbb{C}^{3})^{*})

is a highest weight vector with weight $aL_{1}-bL_{3}$ .