4.18. Lecture 18 ‣ Chapter 4 Representations of 𝔰⁢𝔩_{3,ℂ} ‣ Representation Theory Epiphany

4.18.1. Visualising weights

Shortly we will prove that, if $(\rho,V)$ is a finite dimensional representation of $\mathfrak{sl}_{3,\mathbb{C}}$ , then its weights are integer linear combinations of the $L_{i}$ . In other words, they lie in the weight lattice

\Lambda_{W}=\{a_{1}L_{1}+a_{2}L_{2}+a_{3}L_{3}\,|\,a_{1},a_{2},a_{3}\in\mathbb% {Z}\}.

We want to visualise this in a way that treats $L_{1},L_{2},L_{3}$ symmetrically. Noticing that they sum to zero, we regard them them as the position vectors of the vertices an equilateral triangle with unit side length, centred on the origin. The weight lattice $\Lambda_{W}$ is then the set of vertices of equilateral triangles tiling the plane. For any representation $(\rho,V)$ , its weight diagram is then obtained by circling the weights that occur in that representation.

Example 4.18.1.

We draw the weight diagram for the standard representation, in Figure 4.1.

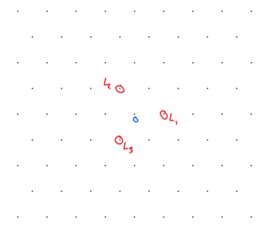
Refer to caption — Figure 4.1. Weights for $\mathbb{C}^{3}$ .

Example 4.18.2.

We draw the weight diagram for the adjoint representation in Figure 4.2. Note that in this case the dimension of the weight space for the weight $0$ is two. We say the weight has multiplicity two, and indicate this on the weight diagram by circling the weight twice. If the multiplicity was much higher, we would need another method (like writing the multiplicity next to the circle as a number).

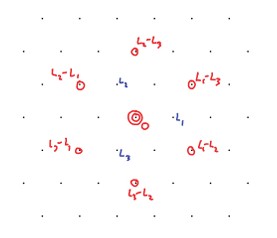
4.18.2. Representations and weights

Firstly, we recall from above that any finite-dimensional representation of $\mathfrak{sl}_{3,\mathbb{C}}$ is completely reducible. This is Theorem 3.14.7 from the previous section, that we proved using the unitary trick.

Theorem 4.18.3.

Let $(\rho,V)$ be a finite-dimensional representation of $\mathfrak{sl}_{3,\mathbb{C}}$ . Then:

(i)

There is a basis of $V$ consisting of weight vectors.
(ii)

Every weight of $V$ is in the weight lattice $\Lambda_{W}$ .

We may combine these two into the single equality

V=\bigoplus_{\alpha\in\Lambda_{W}}V_{\alpha}.

Proof.

Consider the embedding $\iota_{12}:\mathfrak{sl}_{2,\mathbb{C}}\rightarrow\mathfrak{sl}_{3,\mathbb{C}}$ embedding a $2\times 2$ matrix into the ‘top left’ of a $3\times 3$ matrix:

\iota_{12}:\begin{pmatrix}a&b\\ c&-a\end{pmatrix}\longmapsto\begin{pmatrix}a&b&0\\ c&-a&0\\ 0&0&0\end{pmatrix}.

This is a Lie algebra homomorphism, and $\rho\circ\iota_{12}$ is a representation of $\mathfrak{sl}_{2,\mathbb{C}}$ . We know from the $\mathfrak{sl}_{2,\mathbb{C}}$ theory that

(\rho\circ\iota_{12})(H)=\rho\begin{pmatrix}1&&\\ &-1&\\ &&0\end{pmatrix}=\rho(H_{12})

is diagonalisable with integer eigenvalues. If ${\bf v}\in V$ is a weight vector with weight $a_{1}L_{1}+a_{2}L_{2}+a_{3}L_{3}$ , then it is an eigenvector for $\rho(\iota_{12}(H))$ with eigenvalue $a_{1}-a_{2}$ . Thus $a_{1}-a_{2}$ is an integer.

Now, there is another embedding $\iota_{23}$ putting a $2\times 2$ matrix in the ‘bottom right’ corner. The same argument then shows that $\rho(H_{13})$ is diagonalisable with integer eigenvalues, which shows that $a_{2}-a_{3}$ is an integer for every weight.

Thus every weight is in the weight lattice. Moreover, $\rho(H_{12})$ and $\rho(H_{23})$ are diagonalisable, and they commute with each other since $H_{12}$ and $H_{23}$ commute and $\rho$ is a Lie algebra homomorphism. A theorem from linear algebra states that commuting, diagonalisable matrices are simultaneously diagonalisable. It follows that there is a basis of $V$ consisting of simultaneous eigenvectors for $\rho(H_{12})$ and $\rho(H_{23})$ . Since $H_{12}$ and $H_{23}$ span $\mathfrak{h}$ , this is a basis of weight vectors. ∎

Remark 4.18.4.

There is a third homomorphism

\iota_{23}:\begin{pmatrix}a&b\\ c&-a\end{pmatrix}\longmapsto\begin{pmatrix}a&0&b\\ 0&0&0\\ c&0&-a\end{pmatrix}.

We have $\iota_{23}(H)=H_{23}$ .

Note that, for $i<j$ , $\iota_{ij}(X)=E_{ij}$ and $\iota_{ij}(Y)=E_{ji}$ , so $E_{ij}$ and $E_{ji}$ will play the role of raising and lowering operators.

Remark 4.18.5.

We could also prove Theorem 4.18.3 by exponentiating $\rho$ to a representation of $\operatorname{SL}_{3}(\mathbb{C})$ and considering the action of the subgroup of diagonal matrices with entries in $U(1)$ , which is compact (isomorphic to $U(1)$ ). Compare the proof of the statement that the weights of representations of $\mathfrak{sl}_{2,\mathbb{C}}$ are integers (a combination of Theorem 3.13.9(ii) and Theorem 3.14.7).

4.18.3. Tensor constructions

We record how the various linear algebra constructions we know about interact with the theory of weights. If $(\rho,V)$ is a representation of $\mathfrak{g}$ then we consider its weights as a multiset

\{\alpha_{1},\ldots,\alpha_{n}\}

where $n=\dim V$ and each $\alpha\in\mathfrak{h}^{*}$ is written in this list $\dim V_{\alpha}$ — the multiplicity of $\alpha$ — times.

Suppose that $(\sigma,W)$ is another representation of $\mathfrak{g}$ with multiset of weights

\{\beta_{1},\ldots,\beta_{m}\}.

Proposition 4.18.6.

Suppose that $V,W,\alpha_{i},\beta_{j}$ are as above. Then:

(i)

The weights of $V^{*}$ are $\{-\alpha_{1},\ldots,-\alpha_{n}\}$ .
(ii)

The weights of $V\otimes W$ are

$\{\alpha_{i}+\beta_{j}\,|\,1\leq i\leq n,1\leq j\leq m\}.$
(iii)

The weights of $\operatorname{Sym}^{k}(V)$ are

$\{\alpha_{i_{1}}+\ldots+\alpha_{i_{k}}\,|\,1\leq i_{1}\leq i_{2}\leq\ldots\leq i% _{k}\leq n\}.$
(iv)

The weights of $\Lambda^{k}(V)$ are

$\{\alpha_{i_{1}}+\ldots+\alpha_{i_{k}}\,|\,1\leq i_{1}<i_{2}<\ldots<i_{k}\leq n\}.$

Proof.

This is similar to the proof of Proposition 3.12.11 in the $\mathfrak{sl}_{2,\mathbb{C}}$ case and thus is left as an exercise (Problem 4.18.4). ∎

4.18.4. Exercises

.

Problem 49. Show that $a_{1}L_{1}+a_{2}L_{2}+a_{3}L_{3}\in\Lambda_{W}$ if and only if $a_{1}-a_{2},a_{2}-a_{3}\in\mathbb{Z}$ . Must the $a_{i}$ be integers?

Problem 50. The root lattice $\Lambda_{R}\subseteq\Lambda_{W}$ is the subgroup of the weight lattice generated by the roots.

(a)

Draw a picture showing the root lattice inside the weight lattice.
(b)

Show that $\Lambda_{R}$ has index three in $\Lambda_{W}$ (i.e. the quotient $\Lambda_{W}/\Lambda_{R}$ has order three).
(c)

What would the root lattice and weight lattice be for $\mathfrak{sl}_{2,\mathbb{C}}$ ? What is the index in this case?
(d)

Let $V$ be a finite-dimensional irreducible representation of $\mathfrak{sl}_{3,\mathbb{C}}$ . Show that any two weights of $V$ differ by an element of the root lattice.

Problem 51. Prove Proposition 4.18.6

Problem 52. Find the weights of $\operatorname{Sym}^{3}(\mathbb{C}^{3})$ and draw the weight diagram.

Problem 53. Using weights, or otherwise, show that

\mathbb{C}^{3}\otimes(\mathbb{C}^{3})^{*}\cong\mathbb{C}\oplus\mathfrak{sl}_{3% ,\mathbb{C}}

where $\mathbb{C}$ is the trivial representation and $\mathfrak{sl}_{3,\mathbb{C}}$ is the adjoint representation.