Representation Theory IV 2 Representations of Lie groups and Lie algebras - generalities 4 SL₃

3 SL₂

In this section we discuss the finite-dimensional representation theory of the Lie algebra $\mathfrak{sl}_{2,\mathbb{C}}$ . We then use that to study the representation theory of $\operatorname{SL}_{2}(\mathbb{C})$ , $\mathfrak{sl}_{2,\mathbb{R}}$ , $\operatorname{SL}_{2}(\mathbb{R})$ , and $\mathrm{SU}(2)$ , which are all closely related.

3.1 Weights

We fix the following ’standard’ basis of $\mathfrak{sl}_{2,\mathbb{C}}$ :

	$\displaystyle H$	$\displaystyle=\begin{pmatrix}\hidden@noalign{}\hfil\textstyle 1&0\\ \hidden@noalign{}\hfil\textstyle 0&-1\end{pmatrix},$
	$\displaystyle X$	$\displaystyle=\begin{pmatrix}\hidden@noalign{}\hfil\textstyle 0&1\\ \hidden@noalign{}\hfil\textstyle 0&0\end{pmatrix},$
and
	$\displaystyle Y$	$\displaystyle=\begin{pmatrix}\hidden@noalign{}\hfil\textstyle 0&0\\ \hidden@noalign{}\hfil\textstyle 1&0\end{pmatrix}.$

These satisfy the following commutation relations, which are fundamental (check them!):

	$\displaystyle[H,X]$	$\displaystyle=2X,$
	$\displaystyle[H,Y]$	$\displaystyle=-2Y,$
and
	$\displaystyle[X,Y]$	$\displaystyle=H.$

We decompose representations of $\mathfrak{sl}_{2,\mathbb{C}}$ into their eigenspaces for the action of $H$ . The elements $X$ and $Y$ will then move vectors between these eigenspaces, and this will let us analyze the representation theory of $\mathfrak{sl}_{2,\mathbb{C}}$ .

Since $\operatorname{SL}_{2}(\mathbb{C})$ is simply connected, we have

Proposition 3.1.

Every finite-dimensional representation of $\mathfrak{sl}_{2,\mathbb{C}}$ is the derivative of a unique representation of $\operatorname{SL}_{2}(\mathbb{C})$ .

Note that we have not proved this. However, we will use the result freely in what follows. It is possible to give purely algebraic proofs of all the results for which we use the previous proposition, but it is more complicated.

Proposition 3.2.

Let $(\rho,V)$ be a finite-dimensional complex-linear representation of $\mathfrak{sl}_{2,\mathbb{C}}$ . Then $\rho(H)$ is diagonalizable with integer eigenvalues.

Proof.

By the previous proposition $\rho$ is the derivative of a representation $\tilde{\rho}$ of $\operatorname{SL}_{2}(\mathbb{C})$ . We can identify $\operatorname{U}(1)$ as a subgroup of $\operatorname{SL}_{2}(\mathbb{C})$ by the following map:

f:e^{it}\mapsto\begin{pmatrix}e^{it}&\\ &e^{-it}\end{pmatrix}.

By Maschke’s Theorem for $\operatorname{U}(1)$ , $\rho\left(\begin{pmatrix}e^{it}&\\ &e^{-it}\end{pmatrix}\right)$ on $V$ can be diagonalized. Taking the derivative, we see that $\rho\left(\begin{pmatrix}i&0\\ 0&-i\end{pmatrix}\right)$ can be diagonalized and hence so can $\rho(H)=-i\rho\left(\begin{pmatrix}i&0\\ 0&-i\end{pmatrix}\right)$ .

In fact, the classification of irreducible representations of $\operatorname{U}(1)$ shows that $\rho(iH)$ has eigenvalues in $i\mathbb{Z}$ and so $\rho(H)$ has eigenvalues in $\mathbb{Z}$ . ∎

Remark 3.3.

The proof of the proposition is a instance of Weyl’s unitary trick. We turned the action of $H$ , which infinitesimally generates a non-compact one-parameter subgroup of $\operatorname{SL}_{2}(\mathbb{C})$ , into the action of the compact group $\operatorname{U}(1)$ infinitesimally generated by $i H$ . The action of this compact subgroup can be diagonalized.

The proposition does not hold for an arbitrary representation of the one-dimensional Lie algebra $\mathfrak{h}=\mathbb{C}H$ generated by $H$ . Namely, the map $zH\mapsto\begin{pmatrix}1&z\\ 0&1\end{pmatrix}$ cannot be diagonalized. It is implicitly the interaction of $H$ with the other generators $X$ and $Y$ which makes the proposition work.

Let $(\rho,V)$ be a finite-dimensional complex-linear representation of $\mathfrak{sl}_{2,\mathbb{C}}$ . By Proposition 3.2 we get a decomposition

V=\bigoplus_{\alpha}V_{\alpha}

(3.1)

where each $V_{\alpha}$ is the eigenspace for $\rho(H)$ with eigenvalue $\alpha\in\mathbb{C}$ :

V_{\alpha}=\{v\in V:\rho(H)v=\alpha v\}.

Definition 3.4.

1.

Each $\alpha\in\mathbb{C}$ occurring in equation (3.1) is called a weight (more precisely, an $H$ -weight) for the representation $\rho$ .
2.

Each $V_{\alpha}$ is called a weight space for $\rho$ .
3.

The nonzero vectors in $V_{\alpha}$ are called weight vectors for $\rho$ .

Example 3.5.

The set of weights of the zero representation is empty, while the trivial representation has a single weight, $0$ .

Example 3.6.

Let $V=\mathbb{C}^{2}$ be the standard representation. Write $e_{1},e_{-1}$ for the standard basis. Then $He_{1}=e_{1}$ and $He_{-1}=-e_{-1}$ . Thus the set of weights of $V$ is $\{\pm 1\}$ .

Example 3.7.

We consider the adjoint representation $\operatorname{ad}$ of $\mathfrak{g}=\mathfrak{sl}_{2,\mathbb{C}}$ on itself. By the commutation relations, we see directly that $\operatorname{ad}_{H}$ has eigenvalues $0$ ( $[H,H]=0$ ), $2$ ( $[H,X]=2X$ ), and $-2$ ( $[H,Y]=-2Y$ ), so the set of weights is

\{-2,0,2\}.

The non-zero weights $2$ and $-2$ are called the roots of $\mathfrak{sl}_{2,\mathbb{C}}$ and their weight spaces are the root spaces $\mathfrak{g}_{2}$ and $\mathfrak{g}_{-2}$ . The weight vectors are called root vectors.

Thus we have the root space decomposition

	$\displaystyle\mathfrak{sl}_{2,\mathbb{C}}$	$\displaystyle=\mathfrak{g}_{0}\oplus\mathfrak{g}_{2}\oplus\mathfrak{g}_{-2}$
		$\displaystyle=\left\langle H\right\rangle\oplus\left\langle X\right\rangle% \oplus\left\langle Y\right\rangle.$

Example 3.8.

We consider $\mathbb{C}^{2}\otimes\mathbb{C}^{2}$ where $\mathbb{C}^{2}$ is the standard representation. Then

H(e_{1}\otimes e_{1})=(He_{1})\otimes e_{1}+e_{1}\otimes He_{1}=2e_{1}\otimes e% _{1}

and similarly

H(e_{1}\otimes e_{-1})=H(e_{-1}\otimes e_{1})=0,H(e_{-1}\otimes e_{-1})=-2e_{-% 1}\otimes e_{-1}

so that the weights are $\{-2,0,0,2\}$ . Note that this is a multiset — a set with repeated elements — and we say that the weight 0 has ‘multiplicity two’ (in general, the multiplicity of a weight is the dimension of the weight space).

Example 3.9.

Take $V=\operatorname{Sym}^{k}(\mathbb{C}^{2})$ . A set of basis vectors is

\{e_{1}^{a}e_{-1}^{b}:a,b\geq 0,a+b=k\}.

We calculate

	$\displaystyle H(e_{1}^{a}e_{-1}^{b})$	$\displaystyle=a(He_{1})e_{1}^{a-1}e_{-1}^{b}+b(He_{-1})e_{1}^{a}e_{-1}^{b-1}$
		$\displaystyle=(a-b)e_{1}^{a}e_{-1}^{b}.$

Thus the weights are (writing $b=k-a$ ):

\{-k,2-k,4-k,\ldots,k-4,k-2,k\}.

We will soon see an explanation for this pattern.

3.1.1 Highest weights

The following is our first version of the fundamental weight calculation.

Lemma 3.10.

Let $(\rho,V)$ be a complex-linear representation of $\mathfrak{sl}_{2,\mathbb{C}}$ . Let $\alpha$ be a weight of $V$ and let $v\in V_{\alpha}$ . Then

X(v)\in V_{\alpha+2}

and

Y(v)\in V_{\alpha-2}.

Thus we have three maps:

	$\displaystyle H$	$\displaystyle:V_{\alpha}\to V_{\alpha}$
	$\displaystyle X$	$\displaystyle:V_{\alpha}\to V_{\alpha+2}$
	$\displaystyle Y$	$\displaystyle:V_{\alpha}\to V_{\alpha-2}.$

Proof.

We have, for $v\in V_{\alpha}$ ,

	$\displaystyle\rho(H)\rho(X)v$	$\displaystyle=[\rho(H),\rho(X)]v+\rho(X)\rho(H)v$
		$\displaystyle=\rho([H,X])v+\rho(X)\rho(H)v$
		$\displaystyle=2\rho(X)v+\alpha\rho(X)v$
		$\displaystyle=(\alpha+2)\rho(X)v.$

So $\rho(X)v\in V_{\alpha+2}$ as required.

The claim about the action of $Y$ is proved similarly. ∎

Definition 3.11.

A vector $v\in V_{\alpha}$ is a highest weight vector if it is a weight vector and if

Xv=0.

In this case we call the weight of $v$ a highest weight.

Lemma 3.12.

Any finite-dimensional complex linear representation $V$ of $\mathfrak{sl}_{2,\mathbb{C}}$ has a highest weight vector.

Proof.

Indeed, let $\alpha$ be the numerically greatest weight of $V$ (there must be one, as $V$ is finite-dimensional) and let $v$ be a weight vector of weight $\alpha$ . Then $X v$ has weight $\alpha+2$ by the fundamental weight calculation, so must be zero as $\alpha$ was maximal. ∎

Example 3.13.

Let $V=\mathbb{C}^{2}\otimes\mathbb{C}^{2}$ . Then the highest weight vectors are $e_{1}\otimes e_{1}$ and $e_{1}\otimes e_{-1}-e_{-1}\otimes e_{1}$ .

These are easily checked to be highest weight vectors — the first is killed by $X$ since $Xe_{1}=0$ , the second becomes

e_{1}\otimes e_{1}-e_{1}\otimes e_{1}=0.

It is left to you to check that there are no further highest weight vectors.

3.2 Classification of representations of sl_2,C.

The key point here is that a highest weight vector must have non-negative integer weight $n$ , and it then generates an irreducible representation of dimension $n+1$ whose isomorphism class is determined by $n$ and which has a very natural basis of weight vectors.

Let $(\rho,V)$ be a complex-linear representation of $\mathfrak{sl}_{2,\mathbb{C}}$ .

Lemma 3.14.

Suppose that $V$ has a highest weight vector $v$ of weight $n$ . Then the subspace $W$ spanned by the vectors

v,Y(v),Y^{2}(v)=Y(Y(v)),\dots

is an $\mathfrak{sl}_{2,\mathbb{C}}$ -invariant subspace of $V$ .

Moreover, $n\geq 0$ , the dimension of $W$ is $n+1$ , $v,Y(v),\ldots,Y^{n}(v)$ are a basis for $W$ , with $Y^{n+1}(v)=0$ .

Proof.

Let $W$ be the span of the $Y^{k}(v)$ . Since the $Y^{k}(v)$ are weight vectors, their span is $H$ -invariant. It is clearly also $Y$ -invariant. So we only need to check the invariance under the $X$ -action. I claim that for all $m\geq 1$ ,

XY^{m}(v)=m(n-m+1)Y^{m-1}(v).

(3.2)

The proof is by induction. The case $m=1$ is:

XY(v)=([X,Y]+YX)v=Hv+Y(Xv)=Hv=nv.

If the formula holds for $m$ , then

$\displaystyle XY^{m+1}(v)$	$\displaystyle=([X,Y]+YX)Y^{m}(v)$
	$\displaystyle=HY^{m}v+Y(XY^{m}v)$
	$\displaystyle=(n-2m)Y^{m}v+m(n-m+1)Y^{m}v$	(induction hypothesis)
	$\displaystyle=(m+1)(n-m)Y^{m}v$

as required.

If $n$ is not a nonnegative integer, then $m(n-m+1)\neq 0$ for all $m$ . So

Y^{m-1}v\neq 0\implies XY^{m}v\neq 0\implies Y^{m}v\neq 0,

whence $Y^{m}v\neq 0$ for all $m$ . As these are weight vectors with distinct weights, they are linearly independent and so span an infinite dimensional subspace.

If $Y^{i}v=0$ for some $0<i\leq n$ , then

0=XY^{i}v=i(n-i+1)Y^{i-1}v

and so $Y^{i-1}v=0$ . Repeating gives that $v=Y^{0}v=0$ , a contradiction.

Now,

XY^{n+1}(v)=(n+1)(n-n)v=0

and so $Y^{n+1}v$ is either zero or a highest weight vector of weight $-(n+2)<0$ . We have already seen that the second possibility cannot happen, so $Y^{n+1}v=0$ .

Thus $W$ is spanned by the (nonzero) weight vectors $v,Yv,\ldots,Y^{n}v$ with distinct weights, which are therefore linearly independent and so a basis for $W$ . ∎

Remark 3.15.

If we didn’t assume that $V$ was finite-dimensional, then the first part of the previous lemma would still be true.

Corollary 3.16.

In the situation of the previous lemma, $W$ is irreducible.

Proof.

Suppose that $W^{\prime}\subset W$ is a nonzero subrepresentation. Then it has a highest weight vector, which must be (proportional to) $Y^{i}v$ for some $0\leq i\leq n$ . But then

XY^{i}v=i(n-i+1)Y^{i-1}v\neq 0

if $i>0$ and so $i=0$ , meaning that $v\in W^{\prime}$ . But then $Y^{i}v\in W^{\prime}$ for all $i$ , so $W^{\prime}=W$ as required. ∎

The weights of $W$ are illustrated in Figure 3.2.

Theorem 3.17.

Suppose $V$ is an irreducible finite-dimensional complex-linear representation of $\mathfrak{sl}_{2,\mathbb{C}}$ . Then:

1.

There is a unique (up to scalar) highest weight vector, with highest weight $n\geq 0$ .
2.

The weights of $V$ are $n,n-2,\ldots,2-n,-n$ .
3.

All weight spaces $V_{\alpha}$ are one-dimensional (we say that $V$ is ‘multiplicity free’).
4.

The dimension of $V$ is $n+1$ .

For every $n\geq 0$ , there is a unique irreducible complex-linear representation of $\mathfrak{sl}_{2,\mathbb{C}}$ (up to isomorphism) with highest weight $n$ .

Proof.

Let $V$ be an irreducible finite-dimensional complex-linear representation of $\mathfrak{sl}_{2,\mathbb{C}}$ . Let $v\in V$ be a highest weight vector. By Lemma 3.14 its weight is a nonnegative integer $n$ , and by Corollary 3.16 the vectors $v,Yv,\ldots,Y^{n}v$ span an irreducible subrepresentation of $V$ of dimension $n+1$ , which must therefore be the whole of $V$ . The claims all follow immediately.

Moreover, the actions of $X$ , $Y$ and $H$ on this basis are given by explicit matrices depending only on $n$ , so the isomorphism class of $V$ is determined by $n$ .

It remains only to show that a representation with highest weight $n$ exists for all $n\geq 0$ . Consider $\operatorname{Sym}^{n}(\mathbb{C}^{2})$ . The vector $e_{1}^{n}$ is a highest weight vector of weight $n$ , so we are done. In fact, in this case $Y^{a}e_{1}^{n}$ is proportional to $e_{1}^{n-a}e_{-1}^{a}$ , so the irreducible representation generated by $e_{1}^{n}$ is in fact the whole of $\operatorname{Sym}^{n}(\mathbb{C}^{2})$ . ∎

In fact, if $(\rho,V)$ is the irreducible representation with highest weight $n$ , highest weight vector $v$ , then the matrices of $H$ , $Y$ , and $X$ with respect to the basis

\{v,Y(v),\cdots,Y^{n}(v)\}

are respectively

	$\displaystyle\rho(H)$	$\displaystyle=\begin{pmatrix}\hidden@noalign{}\hfil\textstyle n&&&\\ \hidden@noalign{}\hfil\textstyle&n-2&&\\ \hidden@noalign{}\hfil\textstyle&&\ddots&\\ \hidden@noalign{}\hfil\textstyle&&&-n\end{pmatrix},$
	$\displaystyle\rho(Y)$	$\displaystyle=\begin{pmatrix}\hidden@noalign{}\hfil\textstyle 0&&&\\ \hidden@noalign{}\hfil\textstyle 1&0&&\\ \hidden@noalign{}\hfil\textstyle&\ddots&\ddots&\\ \hidden@noalign{}\hfil\textstyle&&1&0\end{pmatrix},$
and
	$\displaystyle\rho(X)$	$\displaystyle=\begin{pmatrix}\hidden@noalign{}\hfil\textstyle 0&n&&&&\\ \hidden@noalign{}\hfil\textstyle&0&2(n-1)&&&\\ \hidden@noalign{}\hfil\textstyle&&0&3(n-2)&&\\ \hidden@noalign{}\hfil\textstyle&&&\ddots&\ddots&\\ \hidden@noalign{}\hfil\textstyle&&&&\ddots&n\\ \hidden@noalign{}\hfil\textstyle&&&&&0\end{pmatrix}.$

Theorem 3.18.

Every finite-dimensional irreducible complex-linear representation of $\operatorname{SL}_{2}(\mathbb{C})$ or $\mathfrak{sl}_{2,\mathbb{C}}$ is isomorphic to $\operatorname{Sym}^{n}(\mathbb{C}^{2})$ , the symmetric power of the standard representation.

Proof.

We already proved this for $\mathfrak{sl}_{2,\mathbb{C}}$ . If $V$ is a representation of $\operatorname{SL}_{2}(\mathbb{C})$ , then its derivative will be isomorphic to $\operatorname{Sym}^{n}(\mathbb{C}^{2})$ . Since $\operatorname{SL}_{2}(\mathbb{C})$ is connected, this implies that $V\cong\operatorname{Sym}^{n}(\mathbb{C}^{2})$ . ∎

3.3 Decomposing representations

Theorem 3.19.

Let $V$ be any finite-dimensional complex-linear representation of $\mathfrak{sl}_{2,\mathbb{C}}$ . Then $V$ is completely reducible, that is, splits into a direct sum of irreducible representations.

Proof.

We will prove this later (Theorem 3.30) using the compact Lie group $\mathrm{SU}(2)$ . ∎

It is easy to decompose a representation $V$ of $\mathfrak{sl}_{2,\mathbb{C}}$ into irreducibles by looking at the weights. Firstly, look at the maximal weight $k$ of $V$ . Then there must be a weight vector $v$ of weight $k$ , which is necessarily a highest weight vector, and so $V$ must contain a copy of $\operatorname{Sym}^{k}(\mathbb{C}^{2})$ — namely, the subspace $\left\langle v,Yv,\ldots,Y^{k}v\right\rangle$ . By complete reducibility we have

V\cong\operatorname{Sym}^{k}(\mathbb{C}^{2})\oplus W.

The weights of $W$ are then obtained by removing the weights of $\operatorname{Sym}^{k}(\mathbb{C}^{2})$ from the weights of $V$ , and we repeat the process.

In particular, this shows that a finite-dimensional representation of $\mathfrak{sl}_{2,\mathbb{C}}$ is determined, up to isomorphism, by its multiset of weights.

Proposition 3.20.

If $V$ , $W$ are representations of $\mathfrak{sl}_{2,\mathbb{C}}$ then:

•

$\{$ weights of $V\otimes W\}=\{$ weights of $V\}+\{$ weights of $W\}$ .
•

$\{$ weights of $\operatorname{Sym}^{k}(V)\}=\{$ sums of unordered $k$ -tuples of weights of $V\}$ .
•

$\{$ weights of $\Lambda^{k}(V)\}=\{$ sums of unordered ‘distinct’ $k$ -tuples of weights of $V\}$ .

Proof.

Omitted: try it yourself! For a similar result, see section 4.5 below. ∎

Example 3.21.

We should illustrate what is meant by ‘distinct’: it is ‘distinct’ as elements of the multiset. Suppose that the weights of $V$ are $\{2,0,0,-2\}$ . Then to obtain the weights of $\Lambda^{2}(V)$ we add together unordered, distinct, pairs of these in every possible way, getting:

\{2+0,2+0,2+-2,0+0,0+-2,0+-2\}=\{2,2,0,0,-2,-2\}.

Example 3.22.

Let $\mathbb{C}^{2}$ be the standard representation of $\operatorname{SL}_{2}(\mathbb{C})$ with weight basis $e_{1}$ , $e_{-1}$ . Consider $V=\operatorname{Sym}^{2}(\mathbb{C}^{2})\otimes\operatorname{Sym}^{2}(\mathbb{% C}^{2})$ . Let $v_{2}=e_{1}^{2}$ , $v_{0}=e_{1}e_{-1}$ and $v_{-2}=e_{-1}^{2}$ be weight vectors in $\operatorname{Sym}^{2}(\mathbb{C}^{2})$ corresponding to the weights $2$ , $0$ and $-2$ . Then the weights of $V$ are

•

$4$ , multiplicity one, weight vector: $v_{2}\otimes v_{2}$ .
•

$2$ , multiplicity two, weight space: $\left\langle v_{2}\otimes v_{0},v_{0}\otimes v_{2}\right\rangle$ .
•

$0$ , multiplicity three, weight space: $\left\langle v_{2}\otimes v_{-2},v_{0}\otimes v_{0},v_{-2}\otimes v_{2}\right\rangle$ .
•

$-2$ , multiplicity two, weight space: $\left\langle v_{0}\otimes v_{-2},v_{-2}\otimes v_{0}\right\rangle$ .
•

$-4$ , multiplicity one, weight vector: $\left\langle v_{-2}\otimes v_{-2}\right\rangle$ .

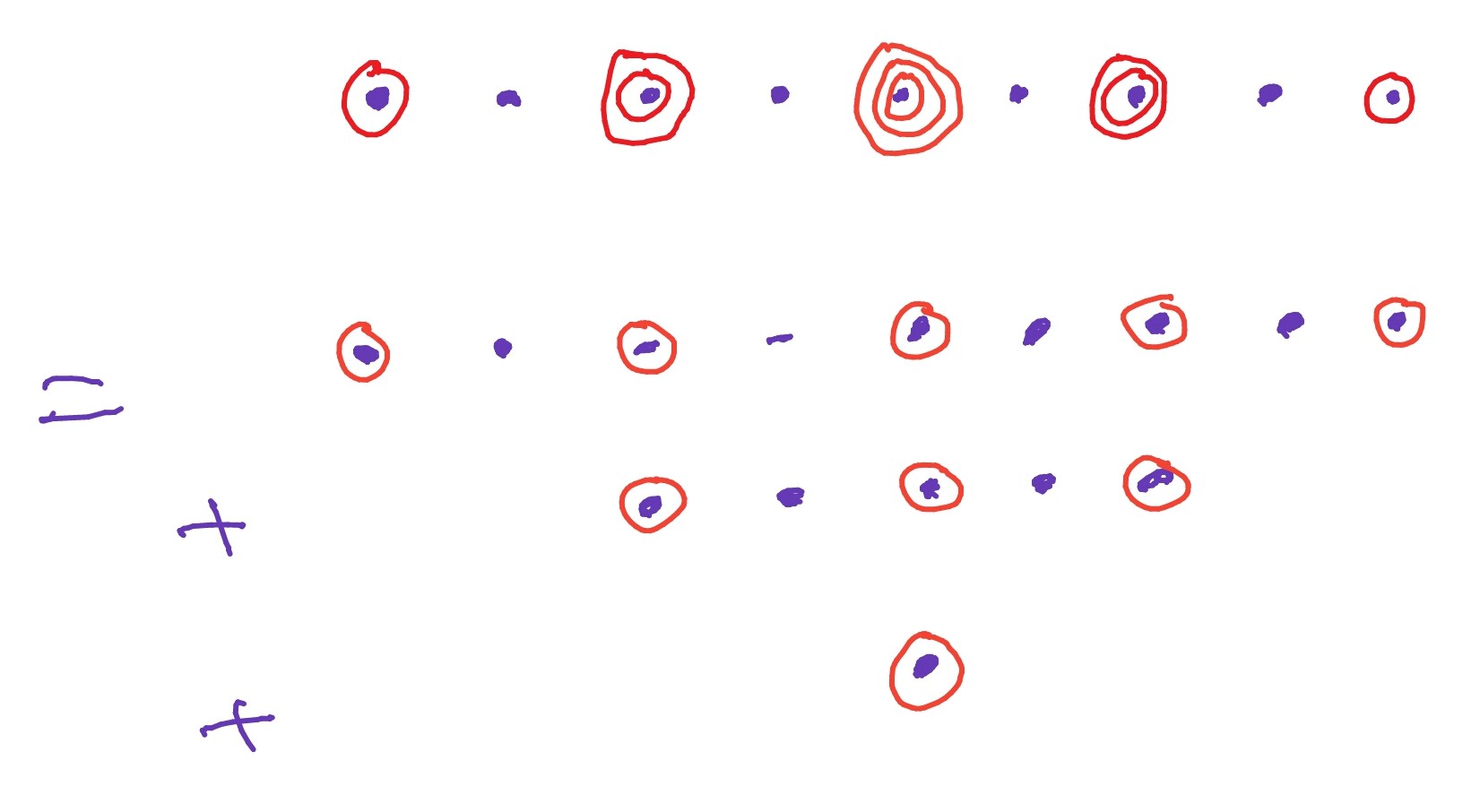
Figure 4: Decomposing $\operatorname{Sym}^{2}(\mathbb{C}^{2})\otimes\operatorname{Sym}^{2}(\mathbb{C}% ^{2})$ .

The weights of $\operatorname{Sym}^{2}(\mathbb{C}^{2})$ are $\{-2,0,2\}$ and so the weights of $V\otimes V$ are

\{-2,0,2\}+\{-2,0,2\}=\{-4,-2,-2,0,0,0,2,2,4\}.

This is the same as the set of weights of

\operatorname{Sym}^{4}(\mathbb{C}^{2})\oplus\operatorname{Sym}^{2}(\mathbb{C}^% {2})\oplus\mathbb{C}

and so this is the required decomposition into irreducibles.

We can go further, and decompose $V$ into irreducible *sub*representations. This means finding irreducible subrepresentations of $V$ such that $V$ is their direct sum.

The copy of $\operatorname{Sym}^{4}(\mathbb{C}^{2})$ in $V$ has highest weight vector $v_{2}\otimes v_{2}$ . We can find a basis by repeatedly hitting this with $Y$ (writing $\propto$ for ‘equal up to a nonzero scalar’):

	$\displaystyle Y(v_{2}\otimes v_{2})$	$\displaystyle=2(v_{2}\otimes v_{0}+v_{0}\otimes v_{2})\propto v_{2}\otimes v_{% 0}+v_{0}\otimes v_{2}$
	$\displaystyle Y^{2}(v_{2}\otimes v_{2})$	$\displaystyle\propto v_{2}\otimes v_{-2}+4v_{0}\otimes v_{0}+v_{-2}\otimes v_{2}$
	$\displaystyle Y^{3}(v_{2}\otimes v_{2})$	$\displaystyle\propto 6(v_{0}\otimes v_{-2}+v_{-2}\otimes v_{0})\propto v_{0}% \otimes v_{-2}+v_{-2}\otimes v_{0}$
	$\displaystyle Y^{4}(v_{2}\otimes v_{2})$	$\displaystyle\propto v_{-2}\otimes v_{-2}.$

These vectors are a basis for the copy of $\operatorname{Sym}^{4}(\mathbb{C}^{2})$ in $V$ .

Next, we find the copy of $\operatorname{Sym}^{2}(\mathbb{C}^{2})$ in $V$ . We start by looking for a highest weight vector of weight 2:

v_{2}\otimes v_{0}-v_{0}\otimes v_{2}

does the trick. Hitting this with $Y$ gives $v_{2}\otimes v_{-2}-v_{-2}\otimes v_{2}$ , and doing so again gives $v_{-2}\otimes v_{0}-v_{0}\otimes v_{-2}$ (up to scalar). These vectors are a basis for the copy of $\operatorname{Sym}^{2}(\mathbb{C}^{2})$ in $V$ .

Finally, we find the trivial representation $\mathbb{C}$ in $V$ . We need only find a weight vector of weight 0 which is killed by $X$ , and

v_{2}\otimes v_{-2}-2v_{0}\otimes v_{0}+v_{-2}\otimes v_{2}

does the job: this vector spans a copy of the trivial representation.

3.4 Real forms and complete decomposability

We use our understanding of the representation theory of $\mathfrak{sl}_{2,\mathbb{C}}$ into an understanding of the representation theory of $\operatorname{SL}_{2}(\mathbb{R})$ and $\mathrm{SU}(2)$ , and prove complete reducibility.

Definition 3.23.

A real form of a complex Lie algebra $\mathfrak{g}$ is a real Lie algebra $\mathfrak{h}\subset\mathfrak{g}$ such that every element $Z$ of $\mathfrak{g}$ can be written uniquely as $X+iY$ for $X,Y\in\mathfrak{h}$ .

Remark 3.24.

In lectures, we didn’t give this definition, just doing the special case of $\mathfrak{su}_{n}\subset\mathfrak{sl}_{n,\mathbb{C}}$ .

For dimension reasons, necessary and sufficient conditions are that $\mathfrak{h}\cap i\mathfrak{h}=0$ and $\dim_{\mathbb{R}}\mathfrak{h}=\dim_{\mathbb{C}}\mathfrak{g}$ .

Example 3.25.

The Lie algebra $\mathfrak{sl}_{n,\mathbb{R}}$ is a real form of $\mathfrak{sl}_{n,\mathbb{C}}$ .

Example 3.26.

The Lie algebra $\mathfrak{su}_{n}$ is a real form of $\mathfrak{sl}_{n,\mathbb{C}}$ . Indeed, $\dim_{\mathbb{R}}\mathfrak{su}_{n}=n^{2}-1=\dim_{\mathbb{C}}\mathfrak{sl}_{n,% \mathbb{C}}$ and if $X,iX\in\mathfrak{su}_{n}$ then

iX=-(iX)^{\dagger}=iX^{\dagger}=-iX

so $X=0$ .

Explicitly, we may write $A\in\mathfrak{sl}_{n,\mathbb{C}}$ as $X+iY$ with

X=\frac{1}{2}(A-A^{\dagger})

and

Y=\frac{-i}{2}(A+A^{\dagger})

in $\mathfrak{su}_{n}$ .

Example 3.27.

Recall that

\mathfrak{so}_{n}=\{A\in{}_{n,\mathbb{R}}:A+A^{T}=0\}.

Let

\mathfrak{so}_{n,\mathbb{C}}=\{A\in{}_{n,\mathbb{C}}:A+A^{T}=0\}.

Since the defining equation $A+A^{T}=0$ can be checked separately on the real and imaginary parts of $A$ ,

\mathfrak{so}_{n,\mathbb{C}}=\{B+iC:B,C\in\mathfrak{so}_{n}\}

and so $\mathfrak{so}_{n}$ is a real form of $\mathfrak{so}_{n,\mathbb{C}}$ .

Proposition 3.28.

Let $\mathfrak{h}$ be a real form of $\mathfrak{g}$ .

There is a one-to-one correspondence between representations of $\mathfrak{h}$ and complex-linear representations of $\mathfrak{g}$ under which irreducible representations correspond to irreducible representations.

Proof.

Given a $\mathbb{C}$ -linear representation of $\mathfrak{g}$ , it is a representation of $\mathfrak{h}$ by restriction. Conversely, if $(\rho,V)$ is a representation of $\mathfrak{h}$ , then it extends to a unique $\mathbb{C}$ -linear representation of $\mathfrak{g}$ given by the formula (forced by $\mathbb{C}$ -linearity)

\rho(X+iY)v=\rho(X)v+i\rho(Y)v.

It is easy to see that this preserves the Lie bracket. The proposition follows (the final statement is left as an exercise). ∎

As a corollary we immediately obtain

Theorem 3.29.

The representation theories of $\mathfrak{sl}_{n,\mathbb{R}}$ and $\mathfrak{su}_{n}$ are ‘the same’ as the complex-linear representation theory of $\mathfrak{sl}_{n,\mathbb{C}}$ . All finite-dimensional irreducible representations of $\mathfrak{sl}_{2,R}$ , $\operatorname{SL}_{2}(\mathbb{R})$ , $\mathfrak{su}_{2}$ , or $\mathrm{SU}(2)$ are of the form $\operatorname{Sym}^{n}(\mathbb{C}^{2})$ .

Proof.

The claims about Lie algebras follow from the above discussion. Every (finite-dimensional) irreducible representation of $\mathfrak{sl}_{2,\mathbb{R}}$ is of the form $\operatorname{Sym}^{n}(\mathbb{C}^{2})$ , and these clearly exponentiate to representations of $\operatorname{SL}_{2}(\mathbb{R})$ , despite this not being a simply connected group! Similarly for $\mathrm{SU}(2)$ (which is simply connected). Since $\operatorname{SL}_{2}(\mathbb{R})$ and $\mathrm{SU}(2)$ are connected, every representation of them is determined by its derivative, so we have a complete list of the irreducible representations. ∎

Theorem 3.30.

Every finite-dimensional complex-linear representation of $\mathfrak{sl}_{n,\mathbb{C}}$ is completely reducible.

Proof.

Let $V$ be a finite-dimensional complex-linear representation of $\mathfrak{sl}_{n,\mathbb{C}}$ and let $W\subset V$ be a subrepresentation. Then $W$ is an $\mathfrak{su}_{n}$ -subrepresentation. As $\mathrm{SU}(n)$ is simply-connected, $V$ and $W$ exponentiate to representations of $\mathrm{SU}(n)$ . Since $\mathrm{SU}(n)$ is compact, by Maschke’s theorem there is a complementary $\mathrm{SU}(n)$ -subrepresentation $W^{\prime}$ with

V=W\oplus W^{\prime}.

Then $W^{\prime}$ is a $\mathfrak{su}_{n}$ -subrepresentation, and so a $\mathbb{C}$ -linear $\mathfrak{sl}_{n,\mathbb{C}}$ -subrepresentation, so that

V=W\oplus W^{\prime}

as representations of $\mathfrak{sl}_{n,\mathbb{C}}$ . Complete reducibility follows. ∎

The argument in this theorem is called Weyl’s unitary trick. For a similar application of this idea, see the proof of Proposition 3.2.

3.5 SO(3) (non-examinable)

We skipped this section, due to the strike, so the material is non-examinable.

3.5.1 Classification of irreducible representations

We have already (see the first problem set this term) seen that $\mathfrak{su}_{2}$ and $\mathfrak{so}_{3}$ are isomorphic. We therefore have:

Theorem 3.31.

There is an irreducible two-dimensional representation $V$ of $\mathfrak{so}_{3}$ (coming from $\mathfrak{so}_{3}\xrightarrow{\sim}\mathfrak{su}_{2}\subset\mathfrak{gl}_{2,% \mathbb{C}}$ ) such that the irreducible complex representations of $\mathfrak{so}_{3}$ are exactly

\operatorname{Sym}^{n}(V)

for $n\geq 0$ .

We want to know which of these representations exponentiate to an irreducible representation of $\mathrm{SO}(3)$ . For this, we revisit the connection with $\mathrm{SU}(2)$ .

Let $\left\langle\cdot,\cdot\right\rangle$ be the bilinear form on $\mathfrak{su}_{2}$ defined by

\left\langle X,Y\right\rangle=-\operatorname{tr}(XY).

Lemma 3.32.

The form $\left\langle\cdot,\cdot\right\rangle$ is a positive definite bilinear form preserved by the adjoint action of $\mathrm{SU}(2)$ .

Proof.

The bilinearity is clear. To see that it is positive definite, if $X\in\mathfrak{su}_{2}$ then

\left\langle X,X\right\rangle=-\operatorname{tr}(X^{2})=\operatorname{tr}(XX^{% \dagger}).

Direct calculation shows $\operatorname{tr}(XX^{\dagger})$ is the sum of the squares of the entries of $X$ , which is strictly positive for nonzero $X$ .

We have, for $g\in\mathrm{SU}(2)$ ,

\left\langle\operatorname{Ad}_{g}X,\operatorname{Ad}_{g}Y\right\rangle=-% \operatorname{tr}(gXg^{-1}gYg^{-1})=-\operatorname{tr}(gXYg^{-1})=-% \operatorname{tr}(XY)

which shows that this inner product is $\mathrm{SU}(2)$ -invariant. ∎

Corollary 3.33.

There is an isomorphism

\mathrm{SU}(2)/\{\pm I\}\to\mathrm{SO}(3).

Proof.

Choosing an orthonormal basis for $\mathfrak{su}_{2}$ with respect to $\left\langle\cdot,\cdot\right\rangle$ identifies the set of linear maps $\mathfrak{su}_{2}\to\mathfrak{su}_{2}$ preserving the inner product with $\mathrm{SO}(3)$ . We therefore have a homomorphism

\mathrm{SU}(2)\to\mathrm{SO}(3)

whose kernel is $\{g\in\mathrm{SU}(2):\operatorname{Ad}_{g}=\operatorname{Ad}\}=\{\pm I\}$ . The derivative of this homomorphism is injective, otherwise there would be a one-parameter subgroup in the kernel of the group homomorphism, and since the Lie algebras have the same dimension we get an isomorphism of Lie algebras. The group homomorphism is therefore surjective, since exponentials of elements of $\mathfrak{so}_{3}$ generate the group $\mathrm{SO}(3)$ . ∎

Remark 3.34.

Let $\mathcal{I},\mathcal{J},\mathcal{K}$ be the elements of $\mathfrak{su}_{2}$ given by

\frac{1}{2}\begin{pmatrix}0&1\\ -1&0\end{pmatrix},\frac{1}{2}\begin{pmatrix}0&i\\ i&0\end{pmatrix},\frac{1}{2}\begin{pmatrix}i&0\\ 0&-i\end{pmatrix}

respectively. Up to scalar, these are an orthonormal basis for $\mathfrak{su}_{2}$ . Since the derivative of the above homomorphism $\mathrm{SU}(2)\to\mathrm{SO}(3)$ is the adjoint map, computed with respect to this basis, we see that the induced isomorphism $\mathfrak{su}_{2}\to\mathfrak{so}_{3}$ takes:

	$\displaystyle\mathcal{I}\mapsto J_{x}$	$\displaystyle=\begin{pmatrix}\hidden@noalign{}\hfil\textstyle 0&0&0\\ \hidden@noalign{}\hfil\textstyle 0&0&-1\\ \hidden@noalign{}\hfil\textstyle 0&1&0\end{pmatrix}$
	$\displaystyle\mathcal{J}\mapsto J_{y}$	$\displaystyle=\begin{pmatrix}\hidden@noalign{}\hfil\textstyle 0&0&1\\ \hidden@noalign{}\hfil\textstyle 0&0&0\\ \hidden@noalign{}\hfil\textstyle-1&0&0\end{pmatrix}$
	$\displaystyle\mathcal{K}\mapsto J_{z}$	$\displaystyle=\begin{pmatrix}\hidden@noalign{}\hfil\textstyle 0&-1&0\\ \hidden@noalign{}\hfil\textstyle 1&0&0\\ \hidden@noalign{}\hfil\textstyle 0&0&0\end{pmatrix}.$

It will be useful to know where this isomorphism takes the elements $H, X, Y$ of $\mathfrak{sl}_{2,\mathbb{C}}=\mathfrak{su}_{2,\mathbb{C}}$ . For example, as $H=-2i\mathcal{K}$ , we see that it goes to $-2iJ_{z}$ . Or, for the lowering operator $Y$ , we have

Y=\begin{pmatrix}0&0\\ 1&0\end{pmatrix}=-(\mathcal{I}+i\mathcal{J})\mapsto-(J_{x}+iJ_{y})

and similarly $X\mapsto J_{x}-iJ_{y}$ .

Corollary 3.35.

For each $\ell\geq 0$ , there is a unique irreducible representation $V^{(\ell)}$ of $\mathrm{SO}(3)$ of dimension $2\ell+1$ .

The derivative of this representation is isomorphic to the representation $\operatorname{Sym}^{2\ell}(V)$ of $\mathfrak{so}_{3}$ .

This gives the complete list of irreducible representations of $\mathrm{SO}(3)$ up to isomorphism.

Proof.

We simply have to work out which representations $\operatorname{Sym}^{k}(V)$ of $\mathfrak{so}_{3}$ exponentiate to a representation of $\mathrm{SO}(3)$ . Since we have

\mathrm{SU}(2)/\{\pm I\}\xrightarrow{\sim}\mathrm{SO}(3)

and each $\operatorname{Sym}^{k}(V)$ exponentiates to a unique representation of $\mathrm{SU}(2)$ — which we also call $\operatorname{Sym}^{k}(V)$ — this is equivalent to asking for which $k$ the centre $\{\pm I\}$ of $\mathrm{SU}(2)$ acts trivially on $\operatorname{Sym}^{k}(V)$ . But we see that $-I$ acts as $(-1)^{k}$ , so the answer is: for even $k$ only.

Thus $\operatorname{Sym}^{k}(V)$ exponentiates to a representation of $\mathrm{SO}(3)$ if, and only if, $k=2\ell$ is even, and we obtain the result. ∎

We can consider the weights of these representations. Under the isomorphism

\mathfrak{su}_{2,\mathbb{C}}=\mathfrak{sl}_{2,\mathbb{C}}\to\mathfrak{so}_{3,% \mathbb{C}}

the element $H=-2i\mathcal{K}$ maps to $-2iJ_{z}$ . Since the $H$ -weights of $V^{(\ell)}$ are $-2\ell,-2(\ell-1),\ldots,2(\ell-1),2\ell$ , we must divide these by $-2i$ to find the weights of $J_{z}$ acting on $V^{(\ell)}$ :

-i\ell,-i(\ell-1),\ldots,i(\ell-1),i\ell.

Example 3.36.

Consider the standard three-dimensional representation of $\mathrm{SO}(3)$ on $\mathbb{C}^{3}$ . The weights of $J_{z}$ are simply its eigenvalues as a $3\times 3$ matrix, which are $-i,0,i$ . We see that this representation is isomorphic to $V^{(1)}$ .

3.5.2 Harmonic functions

We can use our understanding of the representation theory of $\mathrm{SO}(3)$ to shed light on the classical theory of spherical harmonics.

We let $\mathcal{P}^{\ell}$ be the subspace of $\mathbb{C}[x,y,z]$ consisting of homogeneous polynomials of degree $\ell$ . This has an action of $\mathrm{SO}(3)$ given by

(gf)(\mathbf{x})=f(g^{T}\mathbf{x})

where $\mathbf{x}=\begin{pmatrix}x\\ y\\ z\end{pmatrix}$ is a vector in $\mathbb{C}^{3}$ . We therefore get a representation of $\mathrm{SO}(3)$ .

Lemma 3.37.

The elements $J_{x},J_{y}$ , and $J_{z}$ of $\mathrm{SO}(3)$ act on $\mathcal{P}^{\ell}$ according to the following formulae:

	$\displaystyle J_{x}$	$\displaystyle=z\frac{\partial}{\partial y}-y\frac{\partial}{\partial z}$
	$\displaystyle J_{y}$	$\displaystyle=x\frac{\partial}{\partial z}-z\frac{\partial}{\partial x}$
	$\displaystyle J_{z}$	$\displaystyle=y\frac{\partial}{\partial x}-x\frac{\partial}{\partial y}.$

Proof.

Exercise. In fact, prove that the action of $A=(a_{ij})\in\mathfrak{so}_{3}$ is given by

\sum_{i,j}a_{ij}x_{i}\frac{\partial}{\partial x_{j}}

by considering

\frac{d}{dt}f(\exp(tA^{T})\mathbf{x})=\frac{d}{dt}f((I+tA^{T})\mathbf{x})

at $t=0$ (where we rewrite $x, y, z$ as $x_{1},x_{2},x_{3}$ ). ∎

It will be useful in what follows to recall

Lemma 3.38.

(Euler’s formula) If $f$ is a homogeneous polynomial of degree $\ell$ , then

x\frac{\partial}{\partial x}{f}+y\frac{\partial}{\partial y}{f}+z\frac{% \partial}{\partial z}{f}=\ell f.

The representation $\mathcal{P}^{\ell}$ is not irreducible. Let $r^{2}\in\mathbb{C}[x,y,z]$ be the polynomial

r^{2}=x^{2}+y^{2}+z^{2}.

Note that $r^{2}$ is clearly invariant under the action of $\mathrm{SO}(3)$ .

Lemma 3.39.

The map $\mathcal{P}^{\ell}\to\mathcal{P}^{\ell+2}$ defined by

f\mapsto r^{2}f

is an injective homomorphism of $\mathrm{SO}(3)$ -representations.

Proof.

We have, for $g\in\mathrm{SO}(3)$ ,

g(r^{2}f)=g(r^{2})g(f)=r^{2}g(f)

as required. ∎

Next, we consider the Laplace operator:

\Delta f=\frac{\partial^{2}}{\partial x^{2}}+\frac{\partial^{2}}{\partial y^{2% }}+\frac{\partial^{2}}{\partial z^{2}}.

This is map from $\mathcal{P}^{\ell}\to\mathcal{P}^{\ell-2}$ .

Lemma 3.40.

The map $\Delta$ is a map of $\mathrm{SO}(3)$ representations.

Proof.

We must show that, for $g=(g_{ij})\in\mathrm{SO}(3)$ ,

(\Delta f)(g^{T}\mathbf{x})=\Delta(gf)(\mathbf{x})).

We have

\frac{\partial}{\partial x_{i}}(gf)(x)=\sum_{j}g_{ij}\frac{\partial f}{% \partial x_{j}}(g^{T}x)

and so

\frac{\partial}{\partial x_{i}}\frac{\partial}{\partial x_{i}}(gf)(x)=\sum_{j,% k}g_{ij}g_{ik}\frac{\partial}{\partial x_{k}}\frac{\partial}{\partial x_{j}}(g% ^{T}x).

We sum over $i$ , for fixed $j$ and $k$ :

\sum_{i}g_{ij}g_{ik}=\delta_{jk}

since $g$ is orthogonal. We therefore obtain

\sum_{i}\frac{\partial^{2}}{\partial x_{i}^{2}}(gf)(x)=\sum_{j}\frac{\partial^% {2}}{\partial x_{j}^{2}}(f)(g^{T}x),

and therefore

\Delta(gf)=g\Delta(f).

∎

An element $f\in\mathcal{P}^{\ell}$ is harmonic if $\Delta f=0$ . Since $\dim(\mathcal{P}^{\ell})>\dim(\mathcal{P}^{\ell-2})$ , harmonic polynomials must exist. We write $\mathcal{H}^{\ell}\subset\mathcal{P}^{\ell}$ for the space of harmonic polynomials.

Lemma 3.41.

On $\mathcal{P}^{\ell}$ , we have

r^{2}\Delta=J_{x}^{2}+J_{y}^{2}+J_{z}^{2}+\ell^{2}+\ell.

Proof.

Left as an exercise. ∎

It follows that $r^{2}\Delta$ preserves each irreducible subrepresentation of $\mathcal{P}^{\ell}$ (since $J_{x},J_{y},J_{z}$ do). Furthermore, by Schur’s lemma it must act on each irreducible subrepresentation as a scalar. We determine that scalar.

Lemma 3.42.

Suppose that $V\subset\mathcal{P}^{\ell}$ is an irreducible subrepresentation with highest weight $i k$ . Then

(r^{2}\Delta)(f)=(\ell^{2}+\ell-k^{2}-k)f=(\ell-k)(\ell+k+1)f.

Proof.

Since $r^{2}\Delta$ is a $\mathfrak{so}_{3}$ -homomorphism and $V$ is irreducible, by Schur’s lemma it acts as a scalar on $V$ . It therefore suffices to compute the action on a highest weight vector $v\in V$ . So

J_{z}v=ikv,(J_{x}-iJ_{y})v=0.

It follows that $J_{z}^{2}v=-k^{2}v$ and, as

	$\displaystyle J_{x}^{2}+J_{y}^{2}$	$\displaystyle=(J_{x}+iJ_{y})(J_{x}-iJ_{y})+i[J_{x},J_{y}]$
		$\displaystyle=(J_{x}+iJ_{y})(J_{x}-iJ_{y})+iJ_{z},$

we have $(J_{x}^{2}+J_{y}^{2})v=0v-kv$ .

Applying the previous lemma gives the result. ∎

Theorem 3.43.

For every $\ell\geq 0$ ,

\mathcal{P}^{\ell}=\mathcal{H}^{\ell}\oplus r^{2}\mathcal{P}^{\ell-2}.

The space $\mathcal{H}^{\ell}$ is the irreducible highest weight representation of $\mathrm{SO}(3)$ of dimension $2\ell+1$ , and the space $\mathcal{P}^{\ell}$ , as an $\mathrm{SO}(3)$ -representation, is the direct sum of representations of weights $i\ell,i(\ell-2),\ldots$ , each occurring with multiplicity one.

Proof.

We use induction on $\ell$ . The case $\ell=0$ is clear (we just have the trivial representation). Suppose true for $\ell-1$ with $\ell\geq 1$ .

By the previous lemma, the space $\mathcal{H}^{\ell}$ is the sum of all the copies inside $\mathcal{P}^{\ell}$ of the irreducible representation with highest weight $i\ell$ . Since $\mathcal{P}^{\ell-2}$ does not contain this irreducible representation, by the inductive hypothesis, we have

\mathcal{H}^{\ell}\cap r^{2}\mathcal{P}^{\ell-2}=\{0\}.

Since, $\mathcal{H}^{\ell}\neq 0$ as already discussed, its dimension is a positive multiple of $2\ell+1$ . However, its dimension is at most

\dim\mathcal{P}^{\ell}-\dim\mathcal{P}^{\ell-2}=\binom{\ell+2}{2}-\binom{\ell}% {2}=2\ell+1.

It follows that $\mathcal{H}^{\ell}$ is irreducible, and that we have

\mathcal{H}^{\ell}\oplus r^{2}\mathcal{P}^{\ell-2}=\mathcal{P}^{\ell}.

The statement about the decomposition into irreducibles follows. ∎

The proof of this theorem shows that

\mathcal{P}^{\ell}=\mathcal{H}^{\ell}\oplus r^{2}\mathcal{H}^{\ell-2}\oplus r^% {4}\mathcal{P}^{\ell-4}\ldots

so that every polynomial has a unique decomposition as a sum of harmonic polynomials multiplied by powers of $r^{2}$ .

We can go further and give nice bases for the $\mathcal{H}^{\ell}$ by taking weight vectors for $J_{z}$ . First, we have

Lemma 3.44.

The function $(x-iy)^{\ell}\in\mathcal{P}^{\ell}$ is a highest weight vector of weight $i\ell$ .

Proof.

Exercise! ∎

We then obtain a weight basis by repeatedly applying the lowering operator

J_{x}+iJ_{y}=(ix-y)\frac{\partial}{\partial z}{}+z(\frac{\partial}{\partial y}% {}-i\frac{\partial}{\partial x}{}).

The functions thus obtained are known as ’spherical harmonics’ (at least, up to normalization), and give a particularly nice basis for the space of functions on the sphere $S^{2}\subset\mathbb{R}^{3}$ . The decomposition of a function into spherical harmonics is analogous to the Fourier decomposition of a function on the unit circle.

Example 3.45.

If $\ell=1$ , then $\mathcal{P}^{\ell}=\mathcal{H}^{\ell}$ , and the weight vectors are

x+iy,z,x-iy.

If $\ell=2$ , a basis of $\mathcal{H}^{\ell}$ made up of weight vectors is

(x-iy)^{2},z(x-iy),x^{2}+y^{2}-2z^{2},z(x+iy),(x+iy)^{2}.

3 SL2

3.1 Weights

Proposition 3.1.

Proposition 3.2.

Proof.

Remark 3.3.

Definition 3.4.

Example 3.5.

Example 3.6.

Example 3.7.

Example 3.8.

Example 3.9.

3.1.1 Highest weights

Lemma 3.10.

Proof.

Definition 3.11.

Lemma 3.12.

Proof.

Example 3.13.

3.2 Classification of representations of sl2,C.

Lemma 3.14.

Proof.

Remark 3.15.

Corollary 3.16.

Proof.

Theorem 3.17.

Proof.

Theorem 3.18.

Proof.

3.3 Decomposing representations

Theorem 3.19.

Proof.

Proposition 3.20.

Proof.

Example 3.21.

Example 3.22.

3.4 Real forms and complete decomposability

Definition 3.23.

Remark 3.24.

Example 3.25.

Example 3.26.

Example 3.27.

Proposition 3.28.

Proof.

Theorem 3.29.

Proof.

Theorem 3.30.

Proof.

3.5 SO(3) (non-examinable)

3.5.1 Classification of irreducible representations

Theorem 3.31.

Lemma 3.32.

Proof.

Corollary 3.33.

Proof.

Remark 3.34.

Corollary 3.35.

Proof.

Example 3.36.

3.5.2 Harmonic functions

Lemma 3.37.

Proof.

Lemma 3.38.

Lemma 3.39.

Proof.

Lemma 3.40.

Proof.

Lemma 3.41.

Proof.

Lemma 3.42.

Proof.

Theorem 3.43.

Proof.

Lemma 3.44.

Proof.

Example 3.45.

3 SL₂

3.2 Classification of representations of sl_2,C.