Representation Theory IV 3 SL₂ 5 Problems for Epiphany

4 SL₃

We now discuss the finite-dimensional complex-linear representation theory of $\mathfrak{sl}_{3,\mathbb{C}}$ . This then tells us everything about the holomorphic representations of $\operatorname{SL}_{3}(\mathbb{C})$ and, via the machinery of real forms, tells us about representations of $\mathrm{SU}(3)$ and $\operatorname{SL}_{3}(\mathbb{R})$ .

Much of what we say, particularly at first, will generalise in a fairly obvious way to $\mathfrak{sl}_{n,\mathbb{C}}$ .

In this section, all representations of $\mathfrak{sl}_{3,\mathbb{C}}$ will be assumed to be complex-linear.

4.1 The Lie algebra sl_3,C

We study the Lie algebra

\mathfrak{g}=\mathfrak{sl}_{3,\mathbb{C}}=\{X\in\mathfrak{gl}_{3,\mathbb{C}}\;% :\;\operatorname{tr}(X)=0\}

of traceless $3\times 3$ matrices. It has dimension $8$ . We first need to find the analog of the standard basis $H, X, Y$ of $\mathfrak{sl}_{2,\mathbb{C}}$

First, notation: we write $E_{ij}$ for the matrix with a ’1’ in row $i$ and column $j$ , and ’0’ elsewhere. Then $E_{ij}\in\mathfrak{sl}_{3,\mathbb{C}}$ if and only if $i\neq j$ .

The analogue of $H$ will be the entire subalgebra of diagonal matrices.

Definition 4.1.

The (standard) Cartan subalgebra of $\mathfrak{g}$ is $\mathfrak{h}$ , given by

\mathfrak{h}=\left\{\begin{pmatrix}a_{1}&&\\ &a_{2}&\\ &&a_{3}\end{pmatrix}\;:\;a_{1}+a_{2}+a_{3}=0,\right\}.

Note that $\mathfrak{h}$ is an abelian subalgebra, because diagonal matrices commute with each other.

We pick as a basis of $\mathfrak{h}$ the elements

	$\displaystyle H_{12}=E_{11}-E_{22}$	$\displaystyle=\begin{pmatrix}\hidden@noalign{}\hfil\textstyle 1&&\\ \hidden@noalign{}\hfil\textstyle&-1&\\ \hidden@noalign{}\hfil\textstyle&&0\end{pmatrix}$
and
	$\displaystyle H_{23}=E_{22}-E_{33}$	$\displaystyle=\begin{pmatrix}\hidden@noalign{}\hfil\textstyle 0&&\\ \hidden@noalign{}\hfil\textstyle&1&\\ \hidden@noalign{}\hfil\textstyle&&-1\end{pmatrix},$

and also define $H_{13}=E_{11}-E_{33}=H_{12}+H_{23}$ .

Next we consider the adjoint action of $\mathfrak{h}$ on $\mathfrak{g}$ , seeking eigenvectors and eigenvalues. The key calculation is:

\left[\begin{pmatrix}a_{1}&&\\ &a_{2}&\\ &&a_{3}\end{pmatrix},E_{ij}\right]=(a_{i}-a_{j})E_{ij}.

Exercise 4.2.

Check this!

Thus $\{E_{ij}:i\neq j\}\cup\{H_{12},H_{23}\}$ is a basis of simultaneous eigenvectors in $\mathfrak{sl}_{3,\mathbb{C}}$ for the adjoint action of $\mathfrak{h}$ .

4.2 Weights

Suppose that $(\rho,V)$ is a finite-dimensional complex-linear representation of $\mathfrak{sl}_{3,\mathbb{C}}$ . Suppose that $v\in V$ is a simultaneous eigenvector for all $\rho(H)$ , $H\in\mathfrak{h}$ . Then, for each $H\in\mathfrak{h}$ , there is an $\alpha(H)\in\mathbb{C}$ such that $\rho(H)v=\alpha(H)v$ . Since $\rho$ is complex-linear, $\alpha$ is a complex-linear map $\mathfrak{h}\rightarrow\mathbb{C}$ . In other words, $\alpha$ is an element of the dual space $\mathfrak{h}^{*}$ . This motivates the following definition:

Definition 4.3.

Suppose that $(\rho,V)$ is a representation of $\mathfrak{sl}_{3,\mathbb{C}}$ . Then a weight vector in $V$ is $v\in V$ such that there is $\alpha\in\mathfrak{h}^{*}$ (the weight) with:

\rho(H)v=\alpha(H)v

for all $H\in\mathfrak{h}$ .

The weight space of $\alpha$ is

V_{\alpha}=\{v\in V:\rho(H)v=\alpha(H)v\text{ for all $H\in\mathfrak{h}$}\}.

On $\mathfrak{h}$ we have some ‘obvious’ functionals $L_{i}\in\mathfrak{h}^{*}$ given by

L_{i}\left(\begin{smallmatrix}a_{1}&&\\ &a_{2}&\\ &&a_{3}\end{smallmatrix}\right)=a_{i}.

These span $\mathfrak{h}^{*}$ , subject to the relation⁴⁴ 4 More precisely, $\mathfrak{h}^{*}$ is isomorphic to the quotient of the three dimensional vector space with basis $\{L_{1},L_{2},L_{3}\}$ by the subspace spanned by $L_{1}+L_{2}+L_{3}$ .

L_{1}+L_{2}+L_{3}=0.

We compute the weights of some particular representations.

Example 4.4.

If $V=\mathbb{C}^{3}$ is the standard representation of $\mathfrak{sl}_{3,\mathbb{C}}$ (for which $\rho(A)=A$ for all $A\in\mathfrak{sl}_{3,\mathbb{C}}$ ), then the standard basis vectors $e_{1},e_{2},e_{3}$ are all weight vectors:

\begin{pmatrix}a_{1}&&\\ &a_{2}&\\ &&a_{3}\end{pmatrix}e_{i}=a_{i}e_{i}

from which we see that $He_{i}=L_{i}(H)e_{i}$ for all $H\in\mathfrak{h}$ . See table 1.

Weight	$L_{1}$	$L_{2}$	$L_{3}$
Weight vector	$e_{1}$	$e_{2}$	$e_{3}$

Table 1: Weights of the standard representation

Example 4.5.

If $V=(\mathbb{C}^{3})^{*}$ is the dual of the standard representation then it has a basis $e_{1}^{*},e_{2}^{*},e_{3}^{*}$ defined by

e_{i}^{*}(e_{j})=\delta_{ij}.

One can show that $e_{i}^{*}$ is a weight vector of weight $-L_{i}$ , so the weights are $-L_{1},-L_{2},-L_{3}$ . See problem 37.

Example 4.6.

Let $V=\operatorname{Sym}^{2}(\mathbb{C}^{3})$ be the symmetric square of the standard representation. The rules for calculating the weights of $V$ are the same as for $\mathfrak{sl}_{2,\mathbb{C}}$ — so, for the symmetric square, we add all unordered pairs of weights of $\mathbb{C}^{3}$ . For details see section 4.5 The weights of $\mathbb{C}^{3}$ are $\{L_{1},L_{2},L_{3}\}$ and so the weights of $\operatorname{Sym}^{2}(\mathbb{C}^{3})$ are

\{2L_{1},2L_{2},2L_{3},L_{1}+L_{2},L_{2}+L_{3},L_{1}+L_{3}\}.

Note that, if we wanted, we could also write $L_{i}+L_{2}=-L_{3}$ etc.

Example 4.7.

Let $V=\mathfrak{g}$ with the adjoint representation defined by $\rho(X)Y=[X,Y]$ . As already observed, we have

[H,E_{ij}]=L_{i}-L_{j}

for $H\in\mathfrak{h}$ and $i\neq j$ , while $[H,H^{\prime}]=0$ for $H,H^{\prime}\in\mathfrak{h}$ . Thus the weights of the adjoint representation are $L_{i}-L_{j}$ ( $i\neq j$ ) and $0$ . The weight space for $0$ is $\mathfrak{h}$ , which has dimension two with basis $H_{12}$ and $H_{23}$ ; we say that the weight $0$ has multiplicity two in $V$ . We obtain table 2.

\begin{array}[h]{c|ccc}\text{Weight}&\text{Weight space basis}&&\\ \@cline{1-2}\cr\ldelim.{2}{0mm}\ldelim.{3}{0mm}L_{1}-L_{2}&E_{12}&\rdelim\}{3}% {*}\hbox{\multirowsetup\text{Positive roots}}&\rdelim\}{2}{*}\hbox{% \multirowsetup Simple roots}\\ L_{2}-L_{3}&E_{23}\\ L_{1}-L_{3}&E_{13}&\\ \@cline{1-2}\cr\ldelim.{3}{0mm}L_{2}-L_{1}&E_{21}&\rdelim\}{3}{*}\hbox{% \multirowsetup\text{Negative roots}}&\\ L_{3}-L_{2}&E_{32}&\\ L_{3}-L_{1}&E_{31}&\\ \@cline{1-2}\cr 0&H_{12},H_{13}&&\end{array}

Table 2: Weights of the adjoint representation

Definition 4.8.

A root of $\mathfrak{g}=\mathfrak{sl}_{3,\mathbb{C}}$ is a nonzero weight of the adjoint representation. A root vector is a weight vector of a root, and a root space is the weight space of a root.

In other words, a root $\alpha$ with root vector $0\neq E\in\mathfrak{g}$ is a nonzero element $\alpha\in\mathfrak{h}^{*}$ such that

[H,E]=\alpha(H)E.

We write

\Phi=\{\pm(L_{1}-L_{2}),\pm(L_{2}-L_{3}),\pm(L_{1}-L_{3})\}

for the set of roots of $\mathfrak{sl}_{3,\mathbb{C}}$ . Out of these, we call $\Phi^{+}=\{L_{1}-L_{2},L_{2}-L_{3},L_{1}-L_{3}\}$ the positive roots and $\Phi^{-}=\{L_{2}-L_{1},L_{3}-L_{2},L_{3}-L_{1}\}$ the negative roots. We write $\Delta=\{L_{1}-L_{2},L_{2}-L_{3}\}$ ; these are the simple roots. Note that $L_{1}-L_{3}$ is the sum of the two simple roots. We will sometimes write $\alpha_{ij}$ for the root $L_{i}-L_{j}$ .

Finally, we have the root space or Cartan decomposition

\mathfrak{g}=\mathfrak{h}\oplus\bigoplus_{\alpha\in\Phi}\mathfrak{g}_{\alpha},

where the $\mathfrak{g}_{\alpha}$ are the root spaces, which are all one-dimensional.

Exercise 4.9.

Work through all the above theory in the case of $\mathfrak{sl}_{2}$ . What are the roots and root spaces? What is the relation between the weights (as linear functionals on $\mathfrak{h}$ ) and between the weights defined in section 3?

4.3 Visualising weights

Shortly we will prove that, if $(\rho,V)$ is a finite dimensional representation of $\mathfrak{sl}_{3,\mathbb{C}}$ , then its weights are integer linear combinations of the $L_{i}$ . In other words, they lie in the weight lattice

\Lambda_{W}=\{a_{1}L_{1}+a_{2}L_{2}+a_{3}L_{3}:a_{1},a_{2},a_{3}\in\mathbb{Z}\}.

Exercise 4.10.

Show that $a_{1}L_{1}+a_{2}L_{2}+a_{3}L_{3}\in\Lambda_{W}$ if and only if $a_{1}-a_{2},a_{2}-a_{3}\in\mathbb{Z}$ . Must the $a_{i}$ be integers?

We want to visualise this in a way that treats $L_{1},L_{2},L_{3}$ symmetrically. Noticing that they sum to zero, we regard them them as the position vectors of the vertices an equilateral triangle with unit side length, centred on the origin. The weight lattice $\Lambda_{W}$ is then the set of vertices of equilateral triangles tiling the plane. For any representation $(\rho,V)$ , its weight diagram is then obtained by circling the weights that occur in that representation.

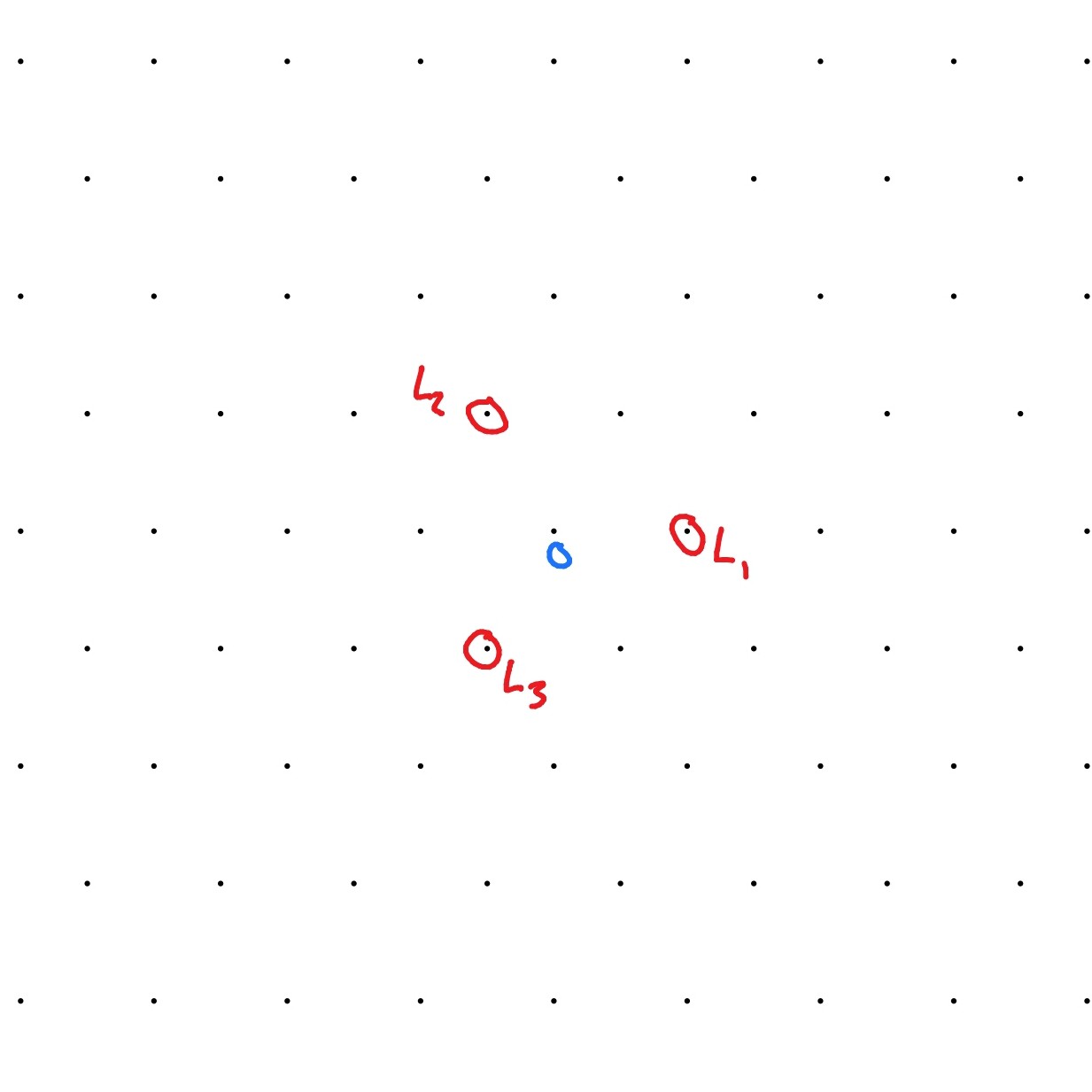
Example 4.11.

We draw the weight diagram for the standard representation, in Figure 5.

Figure 5: Weights for $\mathbb{C}^{3}$ .

Example 4.12.

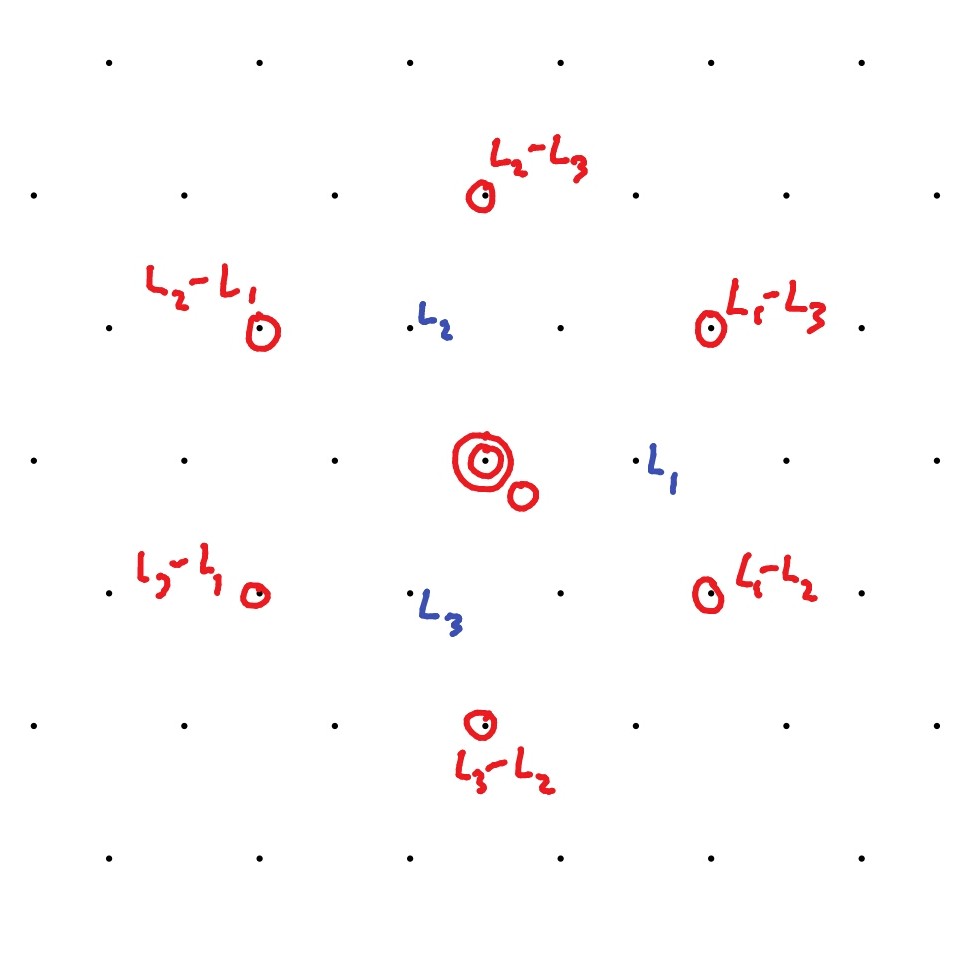
We draw the weight diagram for the adjoint representation in Figure 6. Note that in this case the dimension of the weight space for the weight $0$ is two. We say the weight has multiplicity two, and indicate this on the weight diagram by circling the weight twice. If the multiplicity was much higher, we would need another method (like writing the multiplicity next to the circle as a number).

Figure 6: Weights for the adjoint representation.

4.4 Representations and weights

Firstly, we recall from above that any finite-dimensional representation of $\mathfrak{sl}_{3,\mathbb{C}}$ is completely reducible. This is Theorem 3.30 above, that we proved using the ’unitary trick’.

Theorem 4.13.

Let $(\rho,V)$ be a finite-dimensional representation of $\mathfrak{sl}_{3,\mathbb{C}}$ . Then:

•

There is a basis of $V$ consisting of weight vectors.
•

Every weight of $V$ is in the weight lattice $\Lambda_{W}$ .

We may combine these two into the single equality

V=\bigoplus_{\alpha\in\Lambda_{W}}V_{\alpha}.

Proof.

Consider the embedding $\iota_{12}:\mathfrak{sl}_{2,\mathbb{C}}\rightarrow\mathfrak{sl}_{3,\mathbb{C}}$ embedding a $2\times 2$ matrix into the ‘top left’ of a $3\times 3$ matrix:

\iota_{12}:\begin{pmatrix}a&b\\ c&-a\end{pmatrix}\mapsto\begin{pmatrix}a&b&0\\ c&-a&0\\ 0&0&0\end{pmatrix}.

This is a Lie algebra homomorphism, and $\rho\circ\iota_{12}$ is a representation of $\mathfrak{sl}_{2,\mathbb{C}}$ . We know from the $\mathfrak{sl}_{2,\mathbb{C}}$ theory that

(\rho\circ\iota_{12})(H)=\rho\begin{pmatrix}1&&\\ &-1&\\ &&0\end{pmatrix}=\rho(H_{12})

is diagonalizable with integer eigenvalues. If $v\in V$ is a weight vector with weight $a_{1}L_{1}+a_{2}L_{2}+a_{3}L_{3}$ , then it is an eigenvector for $\rho(\iota_{12}(H))$ with eigenvalue $a_{1}-a_{2}$ . Thus $a_{1}-a_{2}$ is an integer.

Now, there is another embedding $\iota_{23}$ putting a $2\times 2$ matrix in the ‘bottom right’ corner. The same argument then shows that $\rho(H_{13})$ is diagonalisable with integer eigenvalues, which shows that $a_{2}-a_{3}$ is an integer for every weight.

Thus every weight is in the weight lattice. Moreover, $\rho(H_{12})$ and $\rho(H_{23})$ are diagonalizable, and they commute with each other since $H_{12}$ and $H_{23}$ commute and $\rho$ is a Lie algebra homomorphism. A theorem from linear algebra states that commuting, diagonalizable matrices are simultaneously diagonalizable. It follows that there is a basis of $V$ consisting of simultaneous eigenvectors for $\rho(H_{12})$ and $\rho(H_{23})$ . Since $H_{12}$ and $H_{23}$ span $\mathfrak{h}$ , this is a basis of weight vectors. ∎

Remark 4.14.

There is a third homomorphism

\iota_{23}:\begin{pmatrix}a&b\\ c&-a\end{pmatrix}\mapsto\begin{pmatrix}a&0&b\\ 0&0&0\\ c&0&-a\end{pmatrix}.

We have $\iota_{23}(H)=H_{23}$ .

Note that, for $i<j$ , $\iota_{ij}(X)=E_{ij}$ and $\iota_{ij}(Y)=E_{ji}$ , so $E_{ij}$ and $E_{ji}$ will play the role of raising and lowering operators.

Remark 4.15.

We could also prove Theorem 4.13 by exponentiating $\rho$ to a representation of $\operatorname{SL}_{3}(\mathbb{C})$ and considering the action of the subgroup of diagonal matrices with entries in $U(1)$ , which is compact (isomorphic to $U(1)$ ). Compare the proof of the statement that the weights of representations of $\mathfrak{sl}_{2,\mathbb{C}}$ are integers.

4.5 Tensor constructions

We did not go through these proofs in lectures in detail, so I only expect you to know how to apply these results in situations similar to those in lectures or in the problems class.

We record how the various linear algebra constructions we know about interact with the theory of weights. If $(\rho,V)$ is a representation of $\mathfrak{g}$ then we consider its weights as a multiset

\{\alpha_{1},\ldots,\alpha_{n}\}

where $n=\dim V$ and each $\alpha\in\mathfrak{h}^{*}$ is written in this list $\dim V_{\alpha}$ — the multiplicity of $\alpha$ — times.

Suppose that $(\sigma,W)$ is another representation of $\mathfrak{g}$ with multiset of weights

\{\beta_{1},\ldots,\beta_{m}\}.

Theorem 4.16.

Suppose that $V,W,\alpha_{i},\beta_{j}$ are as above. Then:

1.

The weights of $V^{*}$ are $\{-\alpha_{1},\ldots,-\alpha_{n}\}$ .
2.

The weights of $V\otimes W$ are

$\{\alpha_{i}+\beta_{j}:1\leq i\leq n,1\leq j\leq m\}.$
3.

The weights of $\operatorname{Sym}^{k}(V)$ are

$\{\alpha_{i_{1}}+\ldots+\alpha_{i_{k}}:1\leq i_{1}\leq i_{2}\leq\ldots\leq i_{% k}\leq n\}.$
4.

The weights of $\Lambda^{k}(V)$ are

$\{\alpha_{i_{1}}+\ldots+\alpha_{i_{k}}:1\leq i_{1}<i_{2}<\ldots<i_{k}\leq n\}.$

Proof.

Let $v_{1},\ldots,v_{n}$ be a basis of weight vectors of $V$ such that $v_{i}$ has weight $\alpha_{i}$ , and let $w_{1},\ldots,w_{m}$ be similar for $W$ with weights $\beta_{i}$ .

1.

The dual basis $v_{1}^{*},\ldots,v_{n}^{*}$ is a basis of weight vectors in $V^{*}$ with $v_{i}^{*}$ having weight $-\alpha_{i}$ .
2.

If $v$ has weight $\alpha$ and $w$ has weight $\beta$ , then for all $H\in\mathfrak{h}$ ,

$\displaystyle H(v\otimes w)$ $\displaystyle=(Hv\otimes w)+v\otimes(Hw)$

$\displaystyle=\alpha(H)v\otimes w+v\otimes\beta(H)w$

$\displaystyle=(\alpha+\beta)(H)(v\otimes w).$

So $\{v_{i}\otimes w_{j}\}$ is a basis of $V\otimes W$ with the given weights.
3.

Similarly to the previous part,

$\{v_{i_{1}}v_{i_{2}}\ldots v_{i_{k}}:1\leq i_{1}\leq i_{2}\leq\ldots\leq i_{k}% \leq n\}$

is a basis of $\operatorname{Sym}^{k}V$ with the given weights.
4.

Similar.

∎

Remark 4.17.

Similar considerations apply to representations of $\mathfrak{sl}_{2,\mathbb{C}}$ (or $\mathfrak{sl}_{n,\mathbb{C}}$ ).

4.6 Highest weights

We now develop the theory of highest weights, analogous to that for $\mathfrak{sl}_{2,\mathbb{C}}$ . We first carry out the fundamental weight calculation (the analogue of Lemma 3.10).

Lemma 4.18.

(Fundamental Weight Calculation). Let $V$ be a representation of $\mathfrak{sl}_{3,\mathbb{C}}$ and let $v\in V_{\beta}$ be a weight vector with weight $\beta\in\mathfrak{h}^{*}$ . Let $\alpha\in\mathfrak{h}^{*}$ be a root and let $X_{\alpha}\in\mathfrak{g}_{\alpha}$ be a root vector. Then

X_{\alpha}(v)\in V_{\alpha+\beta}.

Thus we obtain a map

X_{\alpha}:V_{\beta}\longrightarrow V_{\alpha+\beta}.

Proof.

Let $H\in\mathfrak{h}$ . Then

H(X(v))=([H,X]+XH)(v)=\alpha(H)X(v)+X(\beta(H)v)=(\alpha+\beta)(H)X(v).\qed

Example 4.19.

We work this out for the adjoint representation. Recall that, for $i\neq j$ , we have the root $\alpha_{ij}=L_{i}-L_{j}$ with root vector $E_{ij}$ . The above calculation shows that, if $\alpha$ and $\beta$ are roots, then $[\mathfrak{g}_{\alpha},\mathfrak{g}_{\beta}]\subset\mathfrak{g}_{\alpha+\beta}$ . Here are some examples:

•

If $\alpha=\alpha_{12}$ , $\beta=\alpha_{13}$ , then $\alpha+\beta$ is not a root so $\mathfrak{g}_{\alpha+\beta}=0$ . Thus $[E_{12},E_{23}]=0$ (which could also be checked directly).
•

If $\alpha=-\beta$ then we get

$[\mathfrak{g}_{\alpha},\mathfrak{g}_{-\alpha}]\subset\mathfrak{g}_{0}=% \mathfrak{h}.$
•

If $\alpha=\alpha_{12}$ , $\beta=\alpha_{23}$ , then $\alpha+\beta=\alpha_{13}$ and we get

$[E_{12},E_{23}]\in\mathfrak{g}_{\alpha_{13}}=\left\langle E_{13}\right\rangle.$

In fact, you can check that $[E_{12},E_{23}]=E_{13}$ .

Exercise 4.20.

Let $V$ be a finite-dimensional irreducible representation of $\mathfrak{sl}_{3,\mathbb{C}}$ . Then the weights occurring in $V$ all differ by integral linear combinations of the roots of $\mathfrak{sl}_{3,\mathbb{C}}$ , that is, by integral linear combinations of $L_{i}-L_{j}$ .

With regard to the weight diagram, we observe that the ’positive’ root vectors $E_{12}$ , $E_{23}$ , $E_{13}$ move in the ’northeast’ direction while the ’negative’ root vectors move in the ’southwest’ direction (roughly speaking). See Figure 7.

Definition 4.21.

Let $(\rho,V)$ be a representation of $\mathfrak{sl}_{3,\mathbb{C}}$ . A highest weight vector in $V$ is a vector $v\in V$ such that:

1.

$v$ is a weight vector; and
2.

$\rho(E_{12})v=\rho(E_{23})v=0$ .

The weight of $v$ is then a highest weight for $V$ .

Remark 4.22.

Since $[E_{12},E_{23}]=E_{13}$ , it follows that a highest weight vector is also killed by $E_{13}$ . So it is killed by all the positive root vectors.

Example 4.23.

1.

The standard representation $V$ has highest weight $L_{1}$ with highest weight vector $e_{1}$ .
2.

The dual $V^{*}$ has highest weight $-L_{3}$ with highest weight vector $e_{3}^{*}$ .
3.

The adjoint representation has highest weight $L_{1}-L_{3}$ with highest weight vector $E_{13}$ .
4.

The symmetric square $\operatorname{Sym}^{2}(\mathbb{C}^{3})$ has highest weight $2L_{1}$ with highest weight vector $e_{1}^{2}$ .

Lemma 4.24.

Let $V$ be a finite-dimensional representation of $\mathfrak{sl}_{3,\mathbb{C}}$ . Then $V$ has a highest weight vector.

Proof.

For a weight $\alpha=\alpha_{1}L_{1}+\alpha_{1}L_{2}+\alpha_{3}L_{3}$ , define $l(\alpha)=\alpha_{1}-\alpha_{3}$ . Of all the finitely many weights of $V$ , choose a weight $\alpha$ such that $l(\alpha)$ is maximal.

Let $v$ be a weight vector with this weight. Then $E_{12}v$ , if nonzero, has weight

\alpha+L_{1}-L_{2}

and

l(\alpha+L_{1}-L_{2})=l(\alpha)+l(L_{1}-L_{2})=l(\alpha)+1>l(\alpha).

This is not a weight of $V$ by maximality of $l(\alpha)$ . Thus $E_{12}v=0$ . Similarly $E_{23}v$ , if nonzero, has weight

\alpha+L_{2}-L_{3}

and $l(\alpha+L_{2}-L_{3})=l(\alpha)+1$ , so $E_{23}v=0$ . ∎

4.7 Weyl symmetry — not examinable

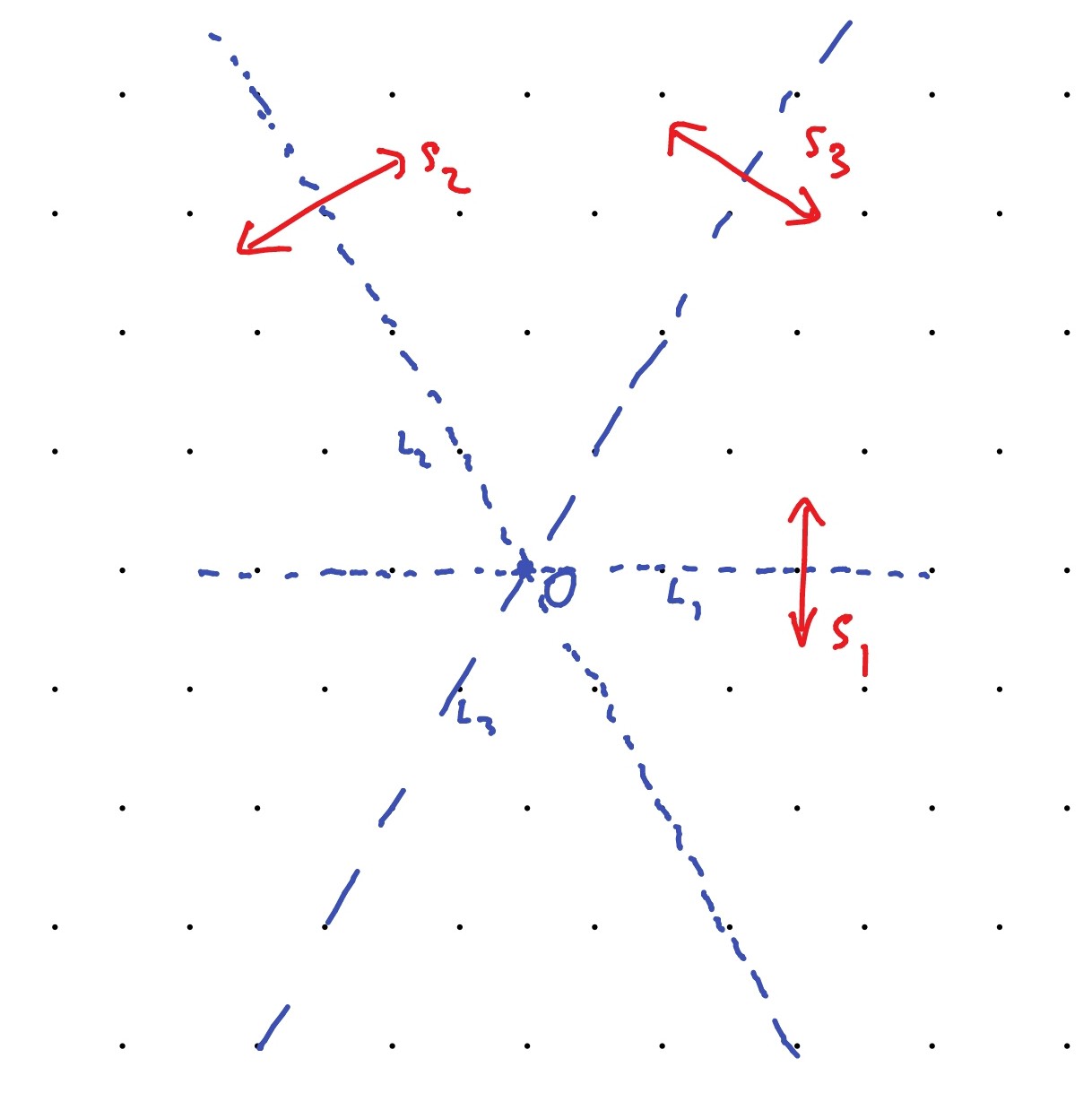
Let $s_{1}$ , $s_{2}$ , and $s_{3}$ be, respectively, reflections in the lines through $L_{1}$ , $L_{2}$ , and $L_{3}$ . Then any two of these (say $s_{1}$ and $s_{3}$ ) generate the Weyl group $W$ , which is the group of symmetries of the triangle with vertices $L_{1},L_{2},L_{3}$ . So we have $W\cong D_{3}\cong S_{3}$ . Note that $W$ acts on the plane in a way that preserves the weight lattice. See Figure 8.

Theorem 4.25.

Let $(\rho,V)$ be a finite-dimensional representation of $\mathfrak{sl}_{3,\mathbb{C}}$ . Then the weights of $V$ are symmetric with respect to the action of the Weyl group.

Proof.

We will prove they are symmetric with respect to $s_{3}$ by using the inclusion

\iota=\iota_{12}:\mathfrak{sl}_{2,\mathbb{C}}\rightarrow\mathfrak{sl}_{3,% \mathbb{C}}

that puts a $2\times 2$ matrix in the top left corner of a $3\times 3$ matrix. We consider the restriction of $V$ to $\mathfrak{sl}_{2,\mathbb{C}}$ .

Note that if $v\in V$ is a weight vector with weight $aL_{1}-bL_{3}$ , then

\rho(\iota(H))v=\rho\left(\begin{pmatrix}1&&\\ &-1&\\ &&0\end{pmatrix}\right)v=av.

Thus $v$ is an $\mathfrak{sl}_{2,\mathbb{C}}$ -weight vector with weight $a$ . Note that $\iota(X)=E_{12}$ , so an $\mathfrak{sl}_{2,\mathbb{C}}$ -weight vector in $V$ is an $\mathfrak{sl}_{2,\mathbb{C}}$ -highest weight vector if it is killed by $E_{12}$ . Note also that $\iota(Y)=E_{21}$ .

The kernel of $E_{12}$ on $V$ is preserved by $\mathfrak{H}$ (check it!) and so has a basis made up of $\mathfrak{sl}_{3,\mathbb{C}}$ -weight vectors $v_{1},\ldots,v_{r}$ . These are then a maximal set of linearly independent highest weight vectors for $\mathfrak{sl}_{2,\mathbb{C}}$ and in particular, if $V_{i}$ is the $\mathfrak{sl}_{2,\mathbb{C}}$ -representation generated by $v_{i}$ then, as an $\mathfrak{sl}_{2,\mathbb{C}}$ -representation,

V=\bigoplus_{i=1}^{r}V_{i}.

Fix $i$ ; it suffices to show that $V_{i}$ has a basis of $\mathfrak{sl}_{3,\mathbb{C}}$ -weight vectors whose weights are preserved by $s_{3}$ . Let $v_{i}$ have weight $aL_{1}-bL_{3}$ . It follows from the $\mathfrak{sl}_{2,\mathbb{C}}$ -theory that $a\geq 0$ and — remembering that $\iota(Y)=E_{21}$ — that $V_{i}$ has a basis

v,E_{21}v,\ldots,E_{21}^{a}v.

By the FWC (Lemma 4.18) we see that these are weight vectors with weights

aL_{1}-bL_{3},(a-1)L_{1}+L_{2}-bL_{3},\ldots,L_{1}+(a-1)L_{2}-bL_{3},aL_{2}-bL% _{3}

which are symmetrical under $s_{3}$ (this reflection swaps $L_{1}$ and $L_{2}$ ), as required. This argument is illustrated in Figure 9

Invariance with respect to the other reflections is proved similarly using the other inclusions $\iota_{ij}$ of $\mathfrak{sl}_{2,\mathbb{C}}$ in $\mathfrak{sl}_{3,\mathbb{C}}$ . ∎

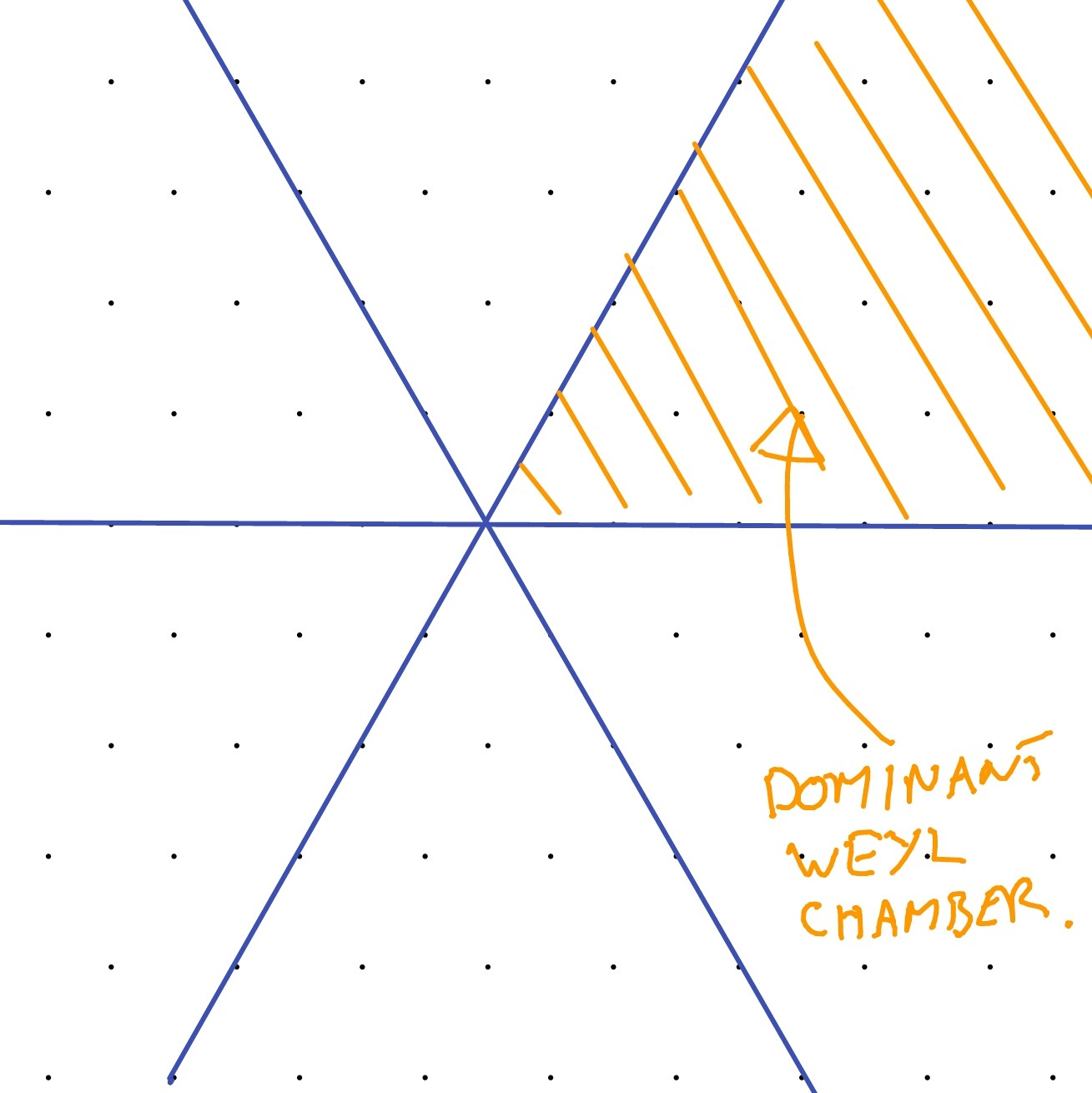
Corollary 4.26.

Every highest weight is of the form $aL_{1}-bL_{3}$ for $a,b\geq 0$ integers. The region

\{aL_{1}-bL_{3}:a,b\in\mathbb{R}_{\geq 0}\}

is called the dominant Weyl chamber and weights inside it (including the boundary) are dominant weights.

Proof.

Indeed, in the course of the proof of Theorem 4.25 we showed that if $aL_{1}-bL_{3}$ was a highest weight, then $a\geq 0$ . A similar argument shows that $b\geq 0$ . ∎

Exercise 4.27.

We can give another proof of Weyl symmetry using the Lie group $\operatorname{SL}_{3}(\mathbb{C})$ . Let $(\rho,V)$ be a representation of $\mathfrak{sl}_{3,\mathbb{C}}$ . As $\operatorname{SL}_{3}(\mathbb{C})$ is simply-connected $\rho$ exponentiates to a representation, $\tilde{\rho}$ , of $\operatorname{SL}_{3}(\mathbb{C})$ . Let

\sigma_{3}=\begin{pmatrix}0&1&0\\ -1&0&0\\ 0&0&1\end{pmatrix}\in\operatorname{SL}_{3}(\mathbb{C}).

Show that, for every weight $\alpha$ , $\tilde{\rho}(\sigma_{3})$ is an isomorphism

V_{\alpha}\rightarrow V_{s_{3}\alpha}.

Give another proof of Theorem 4.25.

4.8 Irreducible representations of sl_3,C.

We are now in a position to state the main theorem of $\mathfrak{sl}_{3,\mathbb{C}}$ -theory.

Theorem 4.28.

For every pair $a, b$ of nonnegative integers, there is a unique (up to isomorphism) irreducible finite-dimensional representation $V^{(a,b)}$ of $\mathfrak{sl}_{3,\mathbb{C}}$ with a highest weight vector of weight $aL_{1}-bL_{3}$ .

Note that the highest weights occurring in the theorem are exactly the dominant elements of the weight lattice.

Since every irreducible finite-dimensional representation does have a highest weight, necessarily dominant, every irreducible representation is isomorphic to $V^{(a,b)}$ for some integers $a,b\geq 0$ .

Example 4.29.

We have already seen some examples:

1.

The standard representation $\mathbb{C}^{3}$ is irreducible with highest weight $L_{1}$ , therefore

$V^{(1,0)}=\mathbb{C}^{3}.$
2.

The dual to the standard representation is irreducible with highest weight $L_{3}$ , and so

$V^{(0,1)}=(\mathbb{C}^{3})^{*}.$
3.

The adjoint representation $\mathfrak{g}$ is irreducible with highest weight $L_{1}-L_{3}$ , and so

$V^{(1,1)}=\mathfrak{g}.$
4.

The symmetric square $\operatorname{Sym}^{2}(\mathbb{C}^{3})$ has highest weight $2L_{1}$ with highest weight vector $e_{1}^{2}$ .

Exercise 4.30.

(Problem 44). Show that, if $V$ is a finite-dimensional representation of $\mathfrak{sl}_{3,\mathbb{C}}$ with a unique highest weight vector (up to scalar), then $V$ is necessarily irreducible.

Deduce that the three representations listed above are indeed irreducible.

For a more general example, we have:

Exercise 4.31.

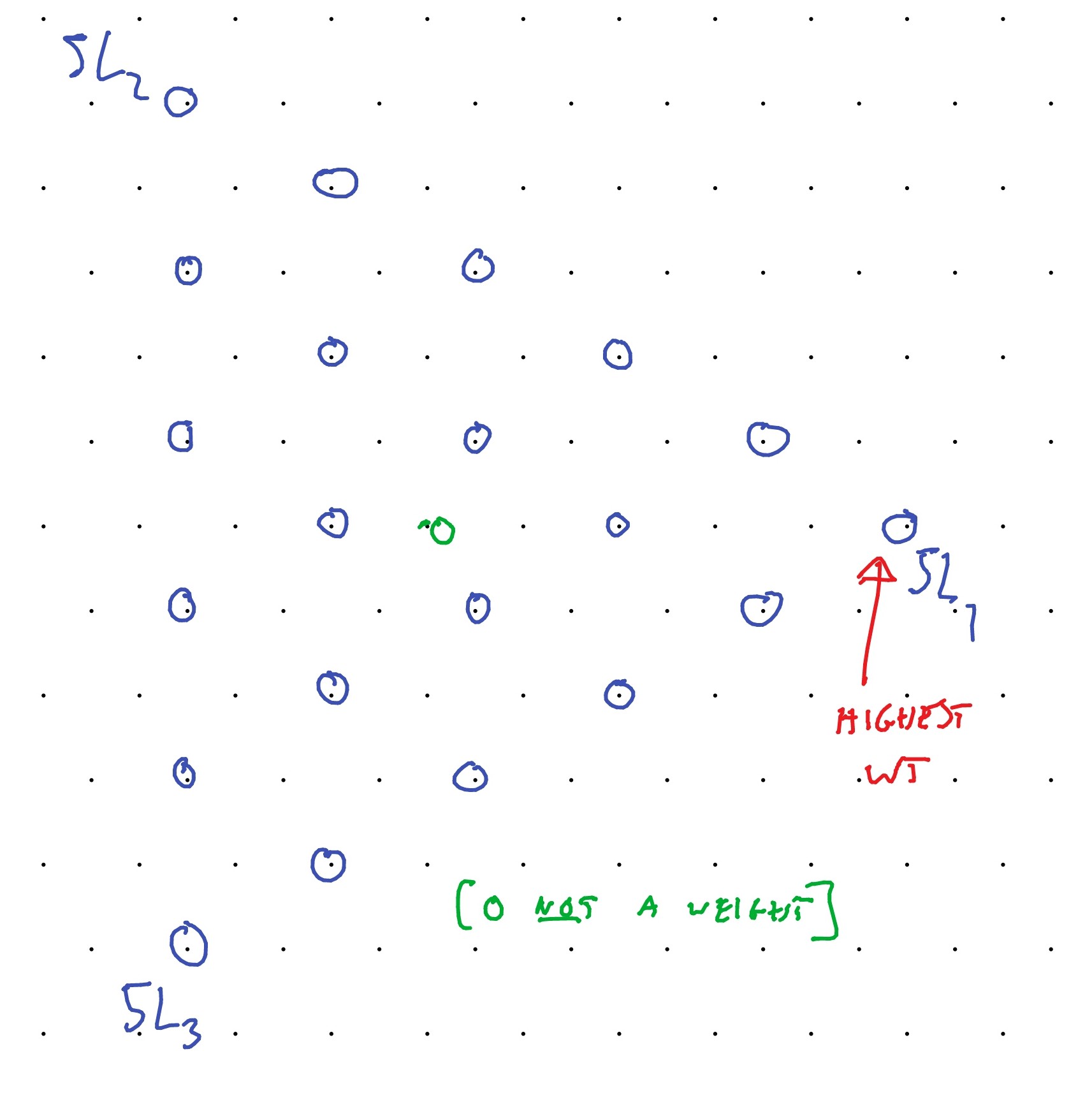
(Problem 46; non-examinable). Show that the representation $\operatorname{Sym}^{n}(\mathbb{C}^{3})$ has a unique highest weight vector with weight $nL_{1}$ . Deduce that

V^{(n,0)}=\operatorname{Sym}^{n}(\mathbb{C}^{3}).

Convince yourself that the weights in this case are as shown in Figure 11 (which illustrates the case $n=5$ ).

4.9 Proof of theorem 4.28 — nonexaminable

Lemma 4.32.

Let $(\rho,V)$ be a finite-dimensional representation of $\mathfrak{sl}_{3,C}$ . Let $v\in V$ be a highest weight vector of weight $\alpha$ , and let

W=\{\rho(Y_{n})\rho(Y_{n-1})\ldots\rho(Y_{1})v:n\geq 0,Y_{i}\in\{E_{21},E_{32}\}.

Then

1.

$W$ is a subrepresentation of $V$
2.

$W_{\alpha}=\left\langle v\right\rangle$ i.e. $v$ is the unique weight vector in $W$ of weight $\alpha$ , up to scaling.
3.

$W$ is irreducible.

Proof.

Let

W_{n}=\{\rho(Y_{m})\rho(Y_{m-1})\ldots\rho(Y_{1})v:n\geq m\geq 0,Y_{i}\in\{E_{% 21},E_{32}\}.

Then

W=\bigcup_{n=0}^{\infty}W_{n}.

Firstly, it is clear that $\rho(E_{21})$ and $\rho(E_{32})$ take $W_{n}$ to $W_{n+1}$ , and so preserve $W$ . Since

\rho(E_{31})=\rho([E_{32},E_{21}])=[\rho(E_{32}),\rho(E_{21})]

we see that $\rho(E_{31})$ also preserves $W$ .

Secondly, every $\rho(Y_{m})\rho(Y_{m-1})\ldots\rho(Y_{1})v$ is a weight vector (by the fundamental weight calculation) and so an eigenvector for all $\rho(H)$ , $H\in\mathfrak{h}$ . Thus $\rho(H)$ preserves each $W_{n}$ (and hence also $W$ ).

Finally, we show that $\rho(E_{12})$ preserves $W_{n}$ . A similar proof then applies for $\rho(E_{23})$ , and then $\rho(E_{13})$ preserves $W$ by the same argument as for $\rho(E_{31})$ . We prove the statement for $\rho(E_{12})$ by induction on $n$ .

For $n=0$ , $W_{0}=\left\langle v\right\rangle$ . Since $v$ is a highest weight vector, $\rho(E_{12})v=0$ and so $\rho(E_{12})(W_{0})\subset W_{0}$ .

Suppose that the claim is true for $n$ . Consider $w=\rho(Y_{n+1})\ldots\rho(Y_{1})v\in W_{n+1}$ with $Y_{i}\in\{E_{21},E_{32}\}$ . We must show that $\rho(E_{12})w\in W_{n+1}$ . Suppose first that $Y_{n+1}=E_{21}$ . Then, as $[E_{12},E_{21}]=H_{12}\in\mathbb{H}$ , we have

	$\displaystyle\rho(E_{12})w$	$\displaystyle=\rho(E_{12})\rho(E_{21})\rho(Y_{n})\ldots\rho(Y_{1})v$
		$\displaystyle=\rho(E_{21})\rho(E_{12})\rho(Y_{n})\ldots\rho(Y_{1})v+\rho(H_{12% })\rho(Y_{n})\ldots\rho(Y_{1})v$
		$\displaystyle\in\rho(E_{21})\rho(E_{12})W_{n}+\rho(H_{12})W_{n}$
		$\displaystyle\subset\rho(E_{21})W_{n}+W_{n}$
by the induction hypothesis and the fact that $W_{n}$ is preserved by $\mathfrak{h}$
		$\displaystyle\subset W_{n+1}+W_{n}$
		$\displaystyle=W_{n+1},$

as required. The proof in the case $Y_{n+1}=E_{32}$ is similar, using that $[E_{12},E_{32}]=0$ .

2.

Note that if $\beta$ the weight of $\rho(Y_{n})\rho(Y_{m-1})\ldots\rho(Y_{1})v$ , with $n$ and $Y_{i}$ as in the lemma, then a calculation using the fundamental weight calculation, as in the proof of lemma [[ref:lem-hwv-exists]], shows that

$l(\beta)=l(\alpha)-n$

and so $\beta\neq\alpha$ if $n>0$ . Since these vectors span $W$ , $v$ is the unique (up to scalar) weight vector in $W$ of weight $\alpha$ .
3.

Suppose that $W$ is reducible. By complete reducibility (Theorem [[ref:thm-complete-reducible-sl]]) we have

$W=U\oplus U^{\prime}$

for $U,U^{\prime}$ nonzero proper subrepresentations of $W$ . We must have $v=u+u^{\prime}$ for unique $u\in U,u^{\prime}\in U^{\prime}$ . The unicity implies that $u$ and $u^{\prime}$ are both weight vectors of weight $\alpha$ ; by part 2, either $u=0$ or $u^{\prime}=0$ . So without loss of generality $v=u\in U$ . But then all $\rho(Y_{n})\ldots\rho(Y_{1})v\in U$ as $U$ is a subrepresentation, so $W=U$ contradicting that $U$ is a proper subrepresentation.

∎

Remark 4.33.

It follows that $W$ as in Lemma 4.32 is actually the subrepresentation generated by $v$ , that is, the span of all vectors obtained by applying arbitrary elements of $\mathfrak{sl}_{3,\mathbb{C}}$ some number of times. The content of the lemma is then that it suffices to apply only $E_{21}$ and $E_{32}$ .

We are now ready to prove Theorem 4.28:

Proof.

First we show the existence. Let $a,b\in\mathbb{Z}_{\geq 0}$ . Consider

V=\operatorname{Sym}^{a}(\mathbb{C}^{3})\otimes\operatorname{Sym}^{b}((\mathbb% {C}^{3})^{*}).

This has a highest weight vector $v=e_{1}^{a}\otimes(e_{3}^{*})^{b}$ of weight $aL_{1}-bL_{3}$ . Let $W$ be the representation generated by $v$ . Then $W$ is irreducible by 4.32 part 3, and has a highest weight vector $v$ of weight $aL_{1}-bL_{3}$ . Thus we can take $V^{(a,b)}=W$ .

Next we show the uniqueness. Suppose that $V, W$ are two irreducible representations with highest weight vectors $v$ and $w$ , respectively, of weight $aL_{1}-bL_{3}$ . Let $U\subset V\oplus W$ be the representation generated by $u=(v,w)$ . Then $U$ is irreducible by 4.32 part 3. The projection $V\oplus W\to V$ sending $(v^{\prime},w^{\prime})$ to $v^{\prime}$ restricts to a homomorphism $U\to V$ which sends $u$ to $v$ . This is therefore a nonzero homomorphism between irreducible representations, and so must be an isomorphism. Thus $U\cong V$ . Similarly $U\cong W$ , and so $V\cong W$ as required. ∎

In fact, it is possible to give an explicit description of the irreducible representations; see problem 47.

Theorem 4.34.

Let $a,b\geq 0$ . Let $V=\mathbb{C}^{3}$

\phi:\operatorname{Sym}^{a}(V)\otimes\operatorname{Sym}^{b}(V^{*})\to% \operatorname{Sym}^{a-1}(V)\otimes\operatorname{Sym}^{b-1}(V^{*})

be the map

(v_{1}\ldots v_{a})\otimes(\lambda_{1}\ldots\lambda_{b})\mapsto\sum_{i=1}^{a}% \sum_{j=1}^{b}\lambda_{j}(v_{i})(v_{1}\ldots\hat{v}_{i}\ldots v_{a})\otimes(% \lambda_{1}\ldots\hat{\lambda_{j}}\ldots\lambda_{b}).

Then $\phi$ is a surjective $\mathfrak{sl}_{3,\mathbb{C}}$ -homomorphism, and its kernel is the irreducible representation with highest weight $aL_{1}-bL_{3}$ .

	$\displaystyle H(v\otimes w)$	$\displaystyle=(Hv\otimes w)+v\otimes(Hw)$
		$\displaystyle=\alpha(H)v\otimes w+v\otimes\beta(H)w$
		$\displaystyle=(\alpha+\beta)(H)(v\otimes w).$

4 SL3

4.1 The Lie algebra sl3,C

Definition 4.1.

Exercise 4.2.

4.2 Weights

Definition 4.3.

Example 4.4.

Example 4.5.

Example 4.6.

Example 4.7.

Definition 4.8.

Exercise 4.9.

4.3 Visualising weights

Exercise 4.10.

Example 4.11.

Example 4.12.

4.4 Representations and weights

Theorem 4.13.

Proof.

Remark 4.14.

Remark 4.15.

4.5 Tensor constructions

Theorem 4.16.

Proof.

Remark 4.17.

4.6 Highest weights

Lemma 4.18.

Proof.

Example 4.19.

Exercise 4.20.

Definition 4.21.

Remark 4.22.

Example 4.23.

Lemma 4.24.

Proof.

4.7 Weyl symmetry — not examinable

Theorem 4.25.

Proof.

Corollary 4.26.

Proof.

Exercise 4.27.

4.8 Irreducible representations of sl3,C.

Theorem 4.28.

Example 4.29.

Exercise 4.30.

Exercise 4.31.

4.9 Proof of theorem 4.28 — nonexaminable

Lemma 4.32.

Proof.

Remark 4.33.

Proof.

Theorem 4.34.

4 SL₃

4.1 The Lie algebra sl_3,C

4.8 Irreducible representations of sl_3,C.