3.15. Lecture 15

3.15.1. Decomposing $\operatorname{Sym}^{2}(\mathbb{C}^{2})\otimes\operatorname{Sym}^{2}(\mathbb{C}% ^{2})$

Example 3.15.1.

Let $\mathbb{C}^{2}$ be the standard representation of $\operatorname{SL}_{2}(\mathbb{C})$ with weight basis ${\bf e}_{1}$ , ${\bf e}_{-1}$ . Consider $V=\operatorname{Sym}^{2}(\mathbb{C}^{2})\otimes\operatorname{Sym}^{2}(\mathbb{% C}^{2})$ . Let ${\bf v}_{2}={\bf e}_{1}^{2}$ , ${\bf v}_{0}={\bf e}_{1}{\bf e}_{-1}$ and ${\bf v}_{-2}={\bf e}_{-1}^{2}$ be weight vectors in $\operatorname{Sym}^{2}(\mathbb{C}^{2})$ corresponding to the weights $2$ , $0$ and $-2$ . Then the weights of $V$ are

•

$4$ , multiplicity one, weight vector: ${\bf v}_{2}\otimes{\bf v}_{2}$ .
•

$2$ , multiplicity two, weight space: $\left\langle{\bf v}_{2}\otimes{\bf v}_{0},{\bf v}_{0}\otimes{\bf v}_{2}\right\rangle$ .
•

$0$ , multiplicity three, weight space: $\left\langle{\bf v}_{2}\otimes{\bf v}_{-2},{\bf v}_{0}\otimes{\bf v}_{0},{\bf v% }_{-2}\otimes{\bf v}_{2}\right\rangle$ .
•

$-2$ , multiplicity two, weight space: $\left\langle{\bf v}_{0}\otimes{\bf v}_{-2},{\bf v}_{-2}\otimes{\bf v}_{0}\right\rangle$ .
•

$-4$ , multiplicity one, weight vector: $\left\langle{\bf v}_{-2}\otimes{\bf v}_{-2}\right\rangle$ .

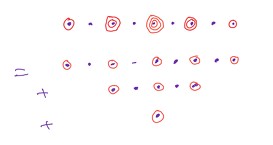
Refer to caption — Figure 3.1. Decomposing $\operatorname{Sym}^{2}(\mathbb{C}^{2})\otimes\operatorname{Sym}^{2}(\mathbb{C}% ^{2})$ .

The weights of $\operatorname{Sym}^{2}(\mathbb{C}^{2})$ are $\{-2,0,2\}$ and so the weights of $\operatorname{Sym}^{2}(\mathbb{C}^{2})\otimes\operatorname{Sym}^{2}(\mathbb{C}% ^{2})$ are

\{-2,0,2\}+\{-2,0,2\}=\{-4,-2,-2,0,0,0,2,2,4\}.

This is the same as the set of weights of

\operatorname{Sym}^{4}(\mathbb{C}^{2})\oplus\operatorname{Sym}^{2}(\mathbb{C}^% {2})\oplus\mathbb{C}

and so this is the required decomposition into irreducibles.

We can go further, and decompose $V$ into irreducible *sub*representations. This means finding irreducible subrepresentations of $V$ such that $V$ is their direct sum (not just isomorphic to their sum).

The copy of $\operatorname{Sym}^{4}(\mathbb{C}^{2})$ in $V$ has highest weight vector ${\bf v}_{2}\otimes{\bf v}_{2}$ . We can find a basis by repeatedly acting with $Y$ on it (writing $\propto$ for ‘equal up to a non-zero scalar’):

	$\displaystyle Y({\bf v}_{2}\otimes{\bf v}_{2})$	$\displaystyle=2({\bf v}_{2}\otimes{\bf v}_{0}+{\bf v}_{0}\otimes{\bf v}_{2})% \propto{\bf v}_{2}\otimes{\bf v}_{0}+{\bf v}_{0}\otimes{\bf v}_{2}$
	$\displaystyle Y^{2}({\bf v}_{2}\otimes{\bf v}_{2})$	$\displaystyle\propto{\bf v}_{2}\otimes{\bf v}_{-2}+4{\bf v}_{0}\otimes{\bf v}_% {0}+{\bf v}_{-2}\otimes{\bf v}_{2}$
	$\displaystyle Y^{3}({\bf v}_{2}\otimes{\bf v}_{2})$	$\displaystyle\propto 6({\bf v}_{0}\otimes{\bf v}_{-2}+{\bf v}_{-2}\otimes{\bf v% }_{0})\propto{\bf v}_{0}\otimes{\bf v}_{-2}\otimes{\bf v}_{-2}\otimes{\bf v}_{0}$
	$\displaystyle Y^{4}({\bf v}_{2}\otimes{\bf v}_{2})$	$\displaystyle\propto{\bf v}_{-2}\otimes{\bf v}_{-2}.$

These vectors are a basis for the copy of $\operatorname{Sym}^{4}(\mathbb{C}^{2})$ in $V$ .

Next, we find the copy of $\operatorname{Sym}^{2}(\mathbb{C}^{2})$ in $V$ . We start by looking for a highest weight vector of weight 2:

{\bf v}_{2}\otimes{\bf v}_{0}-{\bf v}_{0}\otimes{\bf v}_{2}

does the trick. Hitting this with $Y$ gives ${\bf v}_{2}\otimes{\bf v}_{-2}-{\bf v}_{-2}\otimes{\bf v}_{2}$ , and doing so again gives ${\bf v}_{-2}\otimes{\bf v}_{0}-{\bf v}_{0}\otimes{\bf v}_{-2}$ (up to scalar). These vectors are a basis for the copy of $\operatorname{Sym}^{2}(\mathbb{C}^{2})$ in $V$ .

Finally, we find the trivial representation $\mathbb{C}$ in $V$ . We need only find a weight vector of weight 0 which is killed by $X$ , and

{\bf v}_{2}\otimes{\bf v}_{-2}-2{\bf v}_{0}\otimes{\bf v}_{0}+{\bf v}_{-2}% \otimes{\bf v}_{2}

does the job. This vector spans a copy of the trivial representation.

3.15.2. Classification of irreducible $SO(3)$ representations

We have already seen that $\mathfrak{su}_{2}$ and $\mathfrak{so}_{3}$ are isomorphic (Problem 1.5.2). We therefore have:

Theorem 3.15.2.

There is an irreducible two-dimensional representation $V$ of $\mathfrak{so}_{3}$ such that the irreducible complex representations of $\mathfrak{so}_{3}$ are exactly $\operatorname{Sym}^{n}(V)$ for $n\geq 0$ .

Proof.

By Theorem 3.14.6, all irreducible representations of $\mathfrak{su}_{2}$ are of the form $\operatorname{Sym}^{n}(\mathbb{C}^{2})$ for $n\geq 0$ . By the isomorphism from Problem 1.5.2, $\mathfrak{so}_{3}\xrightarrow{\sim}\mathfrak{su}_{2}\subseteq\mathfrak{gl}_{2,% \mathbb{C}}$ , we have that all irreducible representations of $\mathfrak{so}_{3}$ are isomorphic to something of this form. ∎

We want to know which of these representations exponentiate to an irreducible representation of $\mathrm{SO}(3)$ . For this, we revisit the connection with $\mathrm{SU}(2)$ .

Let $\left\langle\cdot,\cdot\right\rangle$ be the bilinear form on $\mathfrak{su}_{2}$ defined by

\left\langle X,Y\right\rangle=-\operatorname{tr}(XY).

Lemma 3.15.3.

The form $\left\langle\cdot,\cdot\right\rangle$ is a positive definite bilinear form preserved by the adjoint action of $\mathrm{SU}(2)$ .

Proof.

This is Problem 1.7.3 where we note that $\operatorname{Ad}_{g}X=gXg^{-1}$ . ∎

Corollary 3.15.4.

There is an isomorphism $\mathrm{SU}(2)/\{\pm\operatorname{Id}\}\cong\mathrm{SO}(3).$

Proof.

Choosing an orthonormal basis for $\mathfrak{su}_{2}$ with respect to $\left\langle\cdot,\cdot\right\rangle$ identifies the set of linear maps $\mathfrak{su}_{2}\to\mathfrak{su}_{2}$ preserving the inner product with $\mathrm{SO}(3)$ . We therefore have a homomorphism

\mathrm{SU}(2)\longrightarrow\mathrm{SO}(3)

whose kernel is $\{g\in\mathrm{SU}(2)\,|\,\operatorname{Ad}_{g}=\operatorname{Id}\}=\{\pm% \operatorname{Id}\}$ . The derivative of this homomorphism is injective, otherwise there would be a one-parameter subgroup in the kernel of the group homomorphism, and since the Lie algebras have the same dimension we get an isomorphism of Lie algebras. The group homomorphism is therefore surjective, since exponentials of elements of $\mathfrak{so}_{3}$ generate the group $\mathrm{SO}(3)$ . ∎

Remark 3.15.5.

Let $\mathcal{I},\mathcal{J},\mathcal{K}$ be the elements of $\mathfrak{su}_{2}$ given by

\frac{1}{2}\begin{pmatrix}0&1\\ -1&0\end{pmatrix},\ \frac{1}{2}\begin{pmatrix}0&i\\ i&0\end{pmatrix},\ \frac{1}{2}\begin{pmatrix}i&0\\ 0&-i\end{pmatrix}

respectively. Up to scalar, these are an orthonormal basis for $\mathfrak{su}_{2}$ . Since the derivative of the above homomorphism $\mathrm{SU}(2)\to\mathrm{SO}(3)$ is the adjoint map, computed with respect to this basis, we see that the induced isomorphism $\mathfrak{su}_{2}\to\mathfrak{so}_{3}$ takes:

	$\displaystyle\mathcal{I}\longmapsto J_{x}$	$\displaystyle=\begin{pmatrix}0&0&0\\ 0&0&-1\\ 0&1&0\end{pmatrix}$
	$\displaystyle\mathcal{J}\longmapsto J_{y}$	$\displaystyle=\begin{pmatrix}0&0&1\\ 0&0&0\\ -1&0&0\end{pmatrix}$
	$\displaystyle\mathcal{K}\longmapsto J_{z}$	$\displaystyle=\begin{pmatrix}0&-1&0\\ 1&0&0\\ 0&0&0\end{pmatrix}.$

It will be useful to know where this isomorphism takes the elements $H,X,Y$ of $\mathfrak{sl}_{2,\mathbb{C}}=\mathfrak{su}_{2,\mathbb{C}}$ . For example, as $H=-2i\mathcal{K}$ , we see that it goes to $-2iJ_{z}$ . Or, for the lowering operator $Y$ , we have

Y=\begin{pmatrix}0&0\\ 1&0\end{pmatrix}=-(\mathcal{I}+i\mathcal{J})\longmapsto-(J_{x}+iJ_{y})

and similarly $X\mapsto J_{x}-iJ_{y}$ .

Corollary 3.15.6.

For each $\ell\geq 0$ , there is a unique irreducible representation $V^{(\ell)}$ of $\mathrm{SO}(3)$ of dimension $2\ell+1$ with derivative isomorphic to the representation $\operatorname{Sym}^{2\ell}(V)$ of $\mathfrak{so}_{3}$ . This gives the complete list of irreducible representations of $\mathrm{SO}(3)$ up to isomorphism.

Proof.

We simply have to work out which irreducible representations $\operatorname{Sym}^{k}(V)$ of $\mathfrak{so}_{3}$ exponentiate to a representation of $\mathrm{SO}(3)$ . Since we have $\mathrm{SU}(2)/\{\pm\operatorname{Id}\}\cong\mathrm{SO}(3)$ and each $\operatorname{Sym}^{k}(V)$ exponentiates to a unique representation of $\mathrm{SU}(2)$ — which we also call $\operatorname{Sym}^{k}(V)$ — this is equivalent to asking for which $k$ the centre $\{\pm\operatorname{Id}\}$ of $\mathrm{SU}(2)$ acts trivially on $\operatorname{Sym}^{k}(V)$ . But we see that $-\operatorname{Id}$ acts as $(-1)^{k}$ , so the answer is for even $k$ only.

Thus $\operatorname{Sym}^{k}(V)$ exponentiates to a representation of $\mathrm{SO}(3)$ if, and only if, $k=2\ell$ is even, and we obtain the result. ∎

We can consider the weights of these representations. Under the isomorphism

\mathfrak{su}_{2,\mathbb{C}}=\mathfrak{sl}_{2,\mathbb{C}}\longrightarrow% \mathfrak{so}_{3,\mathbb{C}}

the element $H=-2i\mathcal{K}$ maps to $-2iJ_{z}$ . Since the $H$ -weights of $V^{(\ell)}$ are $-2\ell,-2(\ell-1),\ldots,2(\ell-1),2\ell$ , we must divide these by $-2i$ to find the weights of $J_{z}$ acting on $V^{(\ell)}$ :

-i\ell,-i(\ell-1),\ldots,i(\ell-1),i\ell.

Example 3.15.7.

Consider the standard three-dimensional representation of $\mathrm{SO}(3)$ on $\mathbb{C}^{3}$ . The weights of $J_{z}$ are simply its eigenvalues as a $3\times 3$ matrix, which are $-i,0,i$ . We see that this representation is isomorphic to $V^{(1)}$ .

3.15.3. Exercises

Problem 40.

(a)

For $a\geq b$ integers, decompose the representation $\operatorname{Sym}^{a}\mathbb{C}^{2}\otimes\operatorname{Sym}^{b}\mathbb{C}^{2}$ of $\mathfrak{sl}_{2,\mathbb{C}}$ into irreducibles. (This is known as the Clebsch–Gordan formula).
(b)

(+) Can you find a general expression for the highest weight vectors for the irreducible subrepresentations? What about for the weight bases?

3.15. Lecture 15

3.15.1. Decomposing Sym2⁡(ℂ2)⊗Sym2⁡(ℂ2)\operatorname{Sym}^{2}(\mathbb{C}^{2})\otimes\operatorname{Sym}^{2}(\mathbb{C}% ^{2})

Example 3.15.1.

3.15.2. Classification of irreducible S⁢O⁢(3)SO(3) representations

Theorem 3.15.2.

Proof.

Lemma 3.15.3.

Proof.

Corollary 3.15.4.

Proof.

Remark 3.15.5.

Corollary 3.15.6.

Proof.

Example 3.15.7.

3.15.3. Exercises

3.15.1. Decomposing $\operatorname{Sym}^{2}(\mathbb{C}^{2})\otimes\operatorname{Sym}^{2}(\mathbb{C}% ^{2})$

3.15.2. Classification of irreducible $SO(3)$ representations